회귀 분석에 관한 포스팅:
https://shacoding.com/2019/12/08/mining-%ed%9a%8c%ea%b7%80-%eb%b6%84%ec%84%9d/

회귀 분석을 이용해서
부모 키에 대한 자식 키의 회귀를 구해 보겠습니다.

install.packages("UsingR")
library(UsingR)
str(galton)

par(mfrow=c(1,2))
hist(galton$child,col="blue",breaks =100)
hist(galton$parent,col="blue",breaks =100)

# 상관지수를 구하는 함수
cor(galton$child,galton$parent)
# 상관지수의 유의성 테스트
cor.test(galton$child,galton$parent)

lm.model=lm(child~parent,data=galton)
lm.model

summary(lm.model)
# r-squared: 모델이 평균 모델보다 얼마나 좋은지
# 1에 가까울수록 좋음

plot(child~parent,data=galton)
abline(lm.model,col="red")

p = data.frame(parent = c(70))
# predict함수를 통해 최적 모델에 대한 예측 값을 구할 수 있음 
predict(lm.model, p)

결과)

0) galton 확인

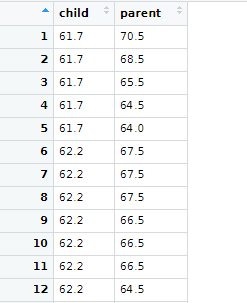
내장 데이터 galton은 (자식의 키와 부모의 키 모음)을 데이터 프레임 형태로 만들었습니다.

1) 자식 키와 부모 키 히스토그램으로 보기

par(mfrow=c(1,2))
hist(galton$child,col="blue",breaks =100)
hist(galton$parent,col="blue",breaks =100)

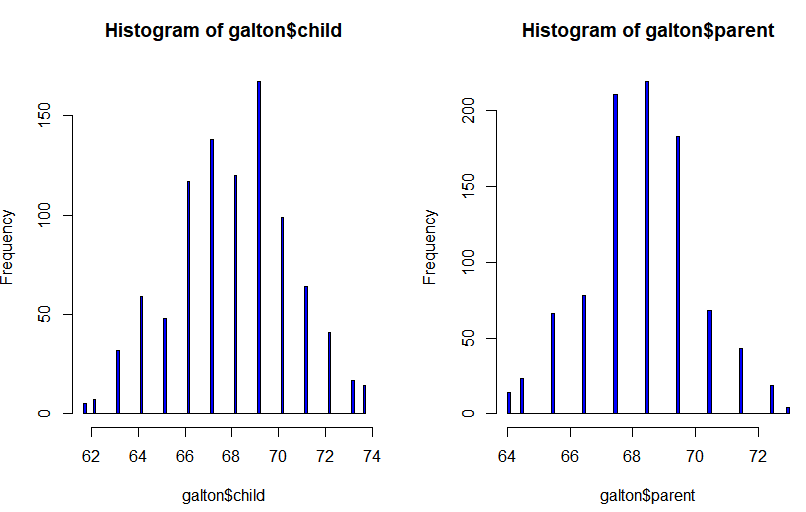
자식 히스토그램과 부모 히스토그램을 한 번에 보기 위해 par(mrfow=c(1,2)을 하였습니다.
위 두 히스토그램만 보고서는 자식 키와 부모 키의 연관성을 알 수가 없습니다.

2) 자식 키와 부모 키로 상관 지수 구하기

# 상관지수를 구하는 함수
cor(galton$child,galton$parent)
# 상관지수의 유의성 테스트
cor.test(galton$child,galton$parent)

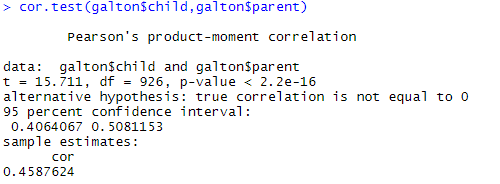
자식 키와 부모 키로 선형 회귀 모델을 만들었을 때, 직선과 점의 가까운 정도는 0.45정도로 보통입니다.
만든 선형 회귀 모델이 그렇게 좋지는 못하다는 것을 보입니다.
직선: (추정) 부모 키에 대한 자식 키를 일반화한 선
점: (실제) 부모 키에 대한 자식 키

3) 선형 회귀 모델 만들기

lm.model=lm(child~parent,data=galton)
lm.model

summary(lm.model)

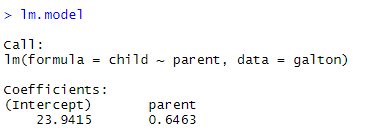
선형 회귀는 R에서 lm함수를 이용해서 모델을 만들 수 있습니다.
첫 번째 인수는 (종속변수~독립변수)가 들어가고, 두 번째 인수는 데이터가 들어갑니다.
그렇게 모델을 만들면 cofficients(계수)가 나옵니다.
y^ = βx + α 에서 베타가 parent이고 알파가 intercept입니다.
=> y^ = 0.6463x + 23.9415

4) 선형 회귀 모델 보기

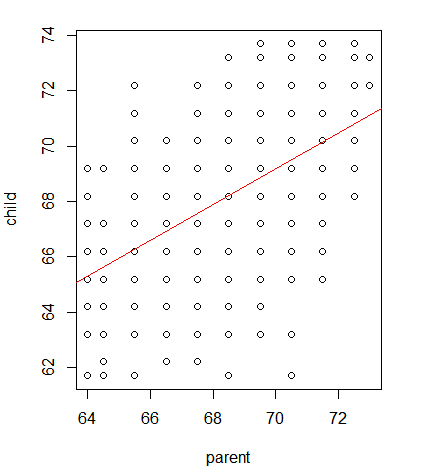
5) 선형 회귀 모델로 예측하기

 p = data.frame(parent = c(70))
# predict함수를 통해 최적 모델에 대한 예측 값을 구할 수 있음 
predict(lm.model, p)

만약 부모 키가 170이면 자식 키는 몇일지 모델을 이용해서 구해 보았습니다.
모델에 결합할 때는 데이터 프레임 형태를 가져야 합니다.
predict함수를 통해 구한 자식의 추정 키는 169입니다.

지금까지 데이터 마이닝의 ‘회귀 분석‘을 알아 보았습니다.