회귀 분석 : 변수와 변수 사이의 관계를 알아보기 위한 통계적 분석 방법
‘종속 변수와 독립 변수 사이의 관계를 알아보기 위한 분석‘ 이라고도 말합니다.
먼저 종속 변수와 독립 변수에 대해 알아 봅시다.
종속 변수는 분석의 대상이 되는 변수입니다.
독립 변수는 종속 변수에 영향을 미치는 변수입니다.
예시를 들어 보겠습니다.
‘부모의 키가 자식의 키에 미치는 영향‘을 분석한다고 해봅시다!
이 때 분석할 변수는 자식의 키입니다. (종속 변수)
자식의 키에 영향을 미치는 변수는 부모의 키입니다. (독립 변수)
회귀 분석에 대한 간략한 소개는 여기까지 하고 아래의 그래프를 보겠습니다.
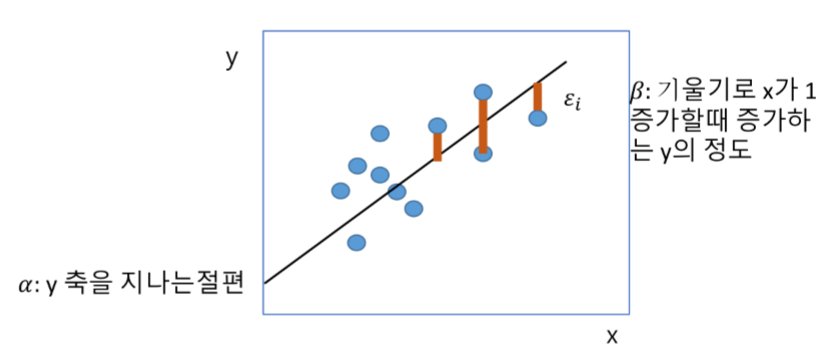
선형 방정식 y = a + bx의 그래프입니다.
위를 단순 선형 회귀 모델이라고 부릅니다.
하나의 종속 변수와 하나의 독립 변수 사이의 관계를 선형 방정식으로 나타낸 것입니다!
독립 변수 x를 c(3.0, 6.0, 9.0, 12.0) 라고 하고
종속 변수 y를 c(3.0, 4.0, 5.5, 6.5) 라고 가정해봅시다!
x = c(3.0, 6.0, 9.0, 12.0) # 독립 변수 y = c(3.0, 4.0, 5.5, 6.5) # 종속 변수 m = lm(y ~ x) # 적합한 모델 찾기 m plot(x,y) abline(m,col="red")
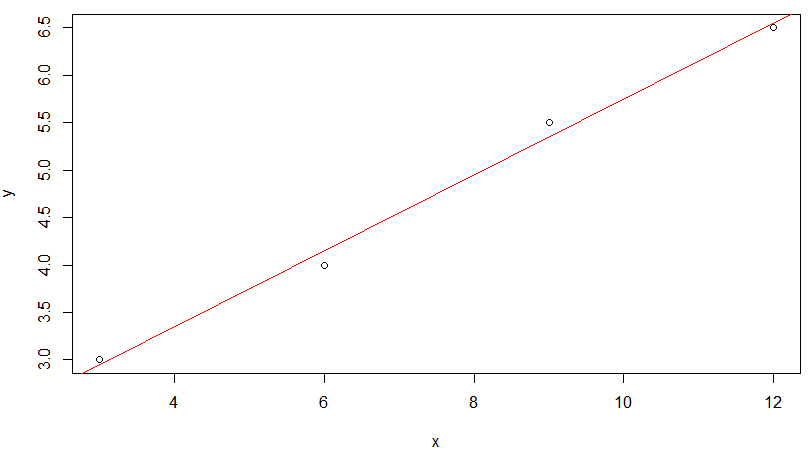
R을 통해 단순 선형 회귀 모델을 만들었을 때,
모든 점이 직선 상에 존재할 수 없는 것을 보입니다.
물론 어떤 종속 변수(y)인가에 따라 직선 상에 존재할 수도 있지만
항상 직선 상에 종속 변수가 있어야 한다는 생각을 버리고 접근해야 합니다.
그렇다면 최적의 모델(직선)은 어떻게 만들까요?
모든 점에서 가장 근접한 선을 그었을 때 최적의 모델이라고 간주합니다!
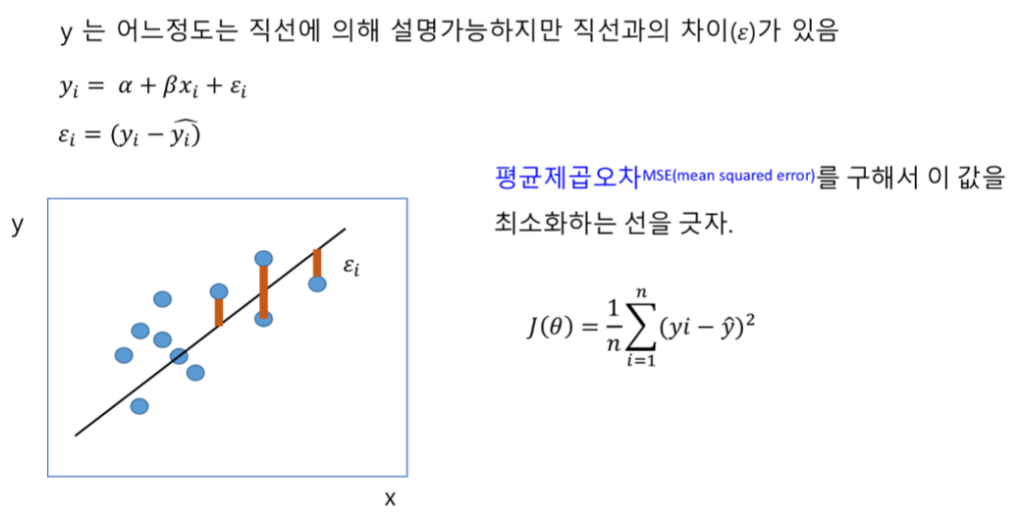
(y^)은 직선을 그었을 때, 해당 선형 방정식의 y값입니다. (y의 추정값이라고 합니다!)
기존의 y값하고는 이미지의 (주황색 선)만큼 차이를 지닙니다.
이 (y-y^)의 차이가 적을 수록 좋은 모델입니다.
그러므로 ‘평균 제곱 오차’ 를 구해서 이 값을 최소화하는 선을 그으면 됩니다.
(y-y^) 는 음수가 될 수도 있으니 제곱을 해서 구합니다.
공식은 아래와 같습니다.
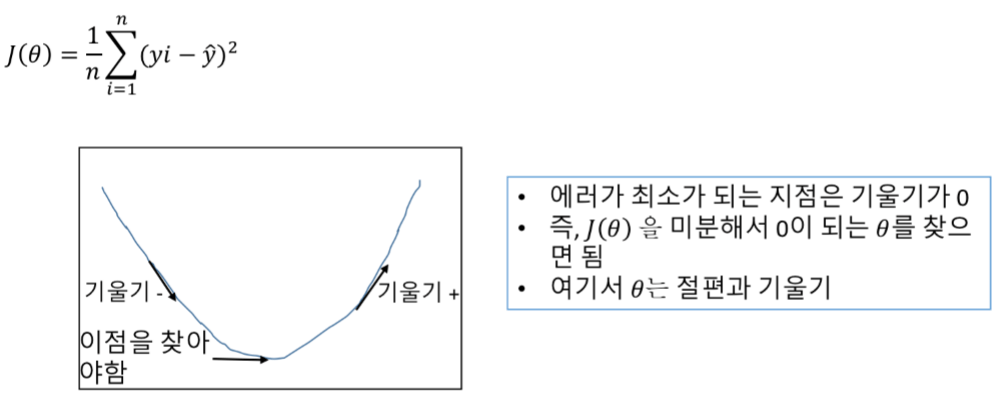
평균 제곱 오차 (J(θ))는 위 그림과 같이 기울기가 0일 때 가장 작습니다.
미분해서 J'( θ)=0인 θ를 구하면 최적의 선을 그릴 수 있습니다.
다른 방법으로 α 와 β를 구할 수도 있습니다.
1) 증명에 의한 도출

β = Sigma(i=1 ->n) { (xi-x평균) *(y-y평균) } / Sigma(i=1 ->n) {(xi-x평균)^2}
α = y평균 – β * x평균
2) 공분산과 분산으로 β 구하기

분산: 편차(x-평균) 제곱의 평균
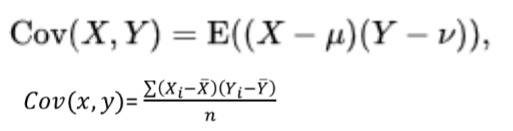
공분산: 두 개의 변수 사이에 얼마나 공통적으로 분산을 가지고 있는가
=> { x편차(x-x평균) * y편차(y-y평균) } 의 평균

회귀 계수: 단순 선형 모델에서 β이며, 직선의 기울기를 나타냄
< 독립 변수의 변동(x분산) 대비 두 변수의 변동(x,y의 공분산)으로 구함>

상관 계수: 변수들의 관계가 직선에 가깝게 따르는 정도, 쉽게 말해서 점과 직선 사이가 얼마나 가깝나의 정도
<두 변수의 변동(x,y의 공분산)을 표준화하기 위해 표준 편차의 곱으로 나눠줌>
0~0.3 : 약한 관계
0.3 ~0.5 : 보통
0.5 이상: 강한 관계
지금까지 단순 선형 회귀를 구하는 방법을 설명했습니다.
이제 다중 선형 회귀로 넘어가겠습니다!
단순 선형 회귀: 독립 변수(x)가 하나인 모델
다중 선형 회귀: 독립 변수(x)가 여러 개인 모델
다중 선형 회귀는 왜 중요할까요?
자식의 키를 분석한다고 했을 때,
독립 변수가 부모의 키뿐일까요?
여러 가지 영양분 섭취나 생활 여건 등 많은 변수가 자식의 키에 영향을 줍니다.
원인이 하나 뿐인 결과는 찾기 힘들기 때문입니다!
단순 선형 회귀 모델이 y^ = βx + α 였다면,
다중 선형 회귀 모델은 y^ = α + (β1*x1) + (β2*x2) + … + (βp*xp)입니다.
<p: 독립 변수의 개수>
위 식에서 a는 미지수기 때문에 (β0*1)로 표현해도 무방합니다.
즉 y^ = (β0*1) + (β1*x1) + (β2*x2) + … + (βp*xp)입니다.
다시 단순 선형 회귀에서 실제 y값은 α + (β *xi)+ ε 였다면,
다중에서 실제 y값은 (β0*1)+ (β1*x[1,i]) + (β2*x[2,i]) + … + (βp*x[p,i]) + εi 입니다.
< ε : (yi-yi^) >
아래 그림을 보고 유추해보시기 바랍니다!
* i는 행렬의 행, p=행렬의 열입니다.
* y식 기준으로 β 벡터는 행벡터(1*p행렬)입니다.
* Y식 기준으로 β 벡터는 열벡터(i*1행렬)이므로 가로로 놓인 (회귀 계수)를 세로로 생각해야 합니다.
yi = (β0*1)+ (β1*x[1,i]) + (β2*x[2,i]) + … + (βp*x[p,i]) + εi
a를 (b0*1)로 바꾼 덕분에 두 가지 이점을 볼 수 있습니다.
1. yi의 일반화된 식 Y = (X행렬 * β벡터 + ε벡터)를 만들 수 있습니다.
2. (β0*1)+ (β1*x[1,i]) + (β2*x[2,i]) + … + (β*x[p,i]) 은 (x i열의 전치 행렬) * β벡터 와 같다고 해서
yi = xi^T * β + εi 로 간결화할 수 있습니다.
Y = Xβ + ε
yi = xi^T * β + εi
위 식에서 β 벡터의 추정값 (β^)은 아래의 공식을 이용합니다.
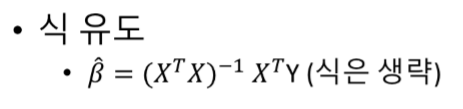
이제 R로 (β^) 를 구하면서 다중 선형 회귀에 대한 설명은 마치겠습니다.
# creating a simple multiple regression function
# 독립변수 x, 종속변수 y
reg<-function(y,x){
x<-as.matrix(x)
# 맨 앞의 모든 값을 모두 1로 하도록 만듦
x<-cbind(Intercept=1,x)
# *는 곱하기, 두 행렬을 곱하려면 %*% 연산자를 사용해야 한다.
# 트랜스포즈는 t()하면 됨, Inverse는 solve함수로 구함
# solve함수는 AX=B일 때 X값을 solve(A,B)로 구하는 함수임
# 두 번째 매개변수의 default값은 항등행렬 I임
# 고로 AX=I일 때 X(A^-1)은 solve(A,I)->solve(A)가 된 것임
b<-solve(t(x) %*%x) %*% t(x) %*% y
colnames(b)<-"estimate"
print(b)
}
이제 모델의 유의성을 구하는 방법을 알아 보겠습니다!
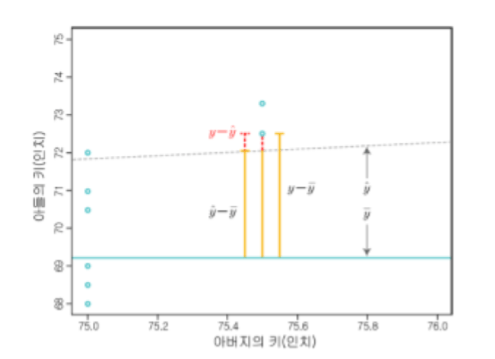
(y- y¯): 실제 y값 – 평균 y값
(y-y^): 실제 y값 – 추정 y값(직선 상의 y값)
(y^-y¯ ): 추정 y값(직선 상의 y값)- 평균 y값
y-y¯ = (y-y^) + (y^-y¯)
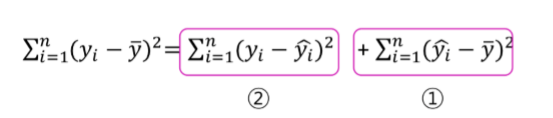
(실제 y값 – 평균y값)의 제곱합 => 전체 변동량(SST)
① : (추정y값-평균y값)의 제곱합 => 회귀제곱합 (SSR)
② : (실제y값-추정y값)의 제곱합 => 오차제곱합 (SSE)
SST = SSE + SSR
자유도와 제곱평균
모든 제곱합, SS는 항상 대응하는 자유도가 있으며, 제곱합을 자유도로 나누어 주면 제곱평균, MS(Mean Square)가 됩니다.
자유도는 통계를 할 때 사용되는 데이터의 양입니다!
SST는 n개의 종속변수 값 중 표본평균 y¯ 를 사용하여 제곱합을 계산하였으므로, 1개의 자유도를 상실하게 되어, 자유도는 n-1이 됩니다.
SSE는 오차를 추정하기 위하여 α 와 β 를 사용하였으므로, 2개의 자유도를 상실하게 되어 자유도는 n-2가 됩니다.
SSR의 자유도는 SST의 자유도에서 SSE의 자유도, 즉 (n-1)-(n-2)=1이 됩니다.
SSE의 제곱 평균 : MSE
=> SSE/ n-2
SSR의 제곱 평균: MSR
=> SSR/1
검정 통계량
단순회귀모형에서 ‘회귀모형이 유의하다’라는 의미는 회귀계수 β≠0이라는 의미와 동일합니다.
즉, 회귀모형의 유의성은 β= 0인지 아니면 β≠0인지를 결정하는 문제로 축소됩니다.
F-검정 : MSR / MSE (회귀제곱평균/오차제곱평균)
영가설: F값이 1보다 작다. (=) 종속 변수와 독립 변수간 선형 관계가 없다. (H0 : β= 0)
대안가설: F값이 1보다 크다. (=) 종속 변수와 독립 변수간 선형 관계가 있다. (H1 : β≠0)
F값이 1보다 큰 값을 가지게 되면, 영가설을 기각하고 대안가설 (H1 : β≠0) 을 받아들이는 결정을 하게 됩니다.
이는 독립변수가 종속변수에 의미있는 영향을 미친다는 것으로 해석할 수 있습니다.

위는 지금까지 설명한 내용을 정리한 표입니다!
모델의 성능을 평가하기

모델의 성능은 (회귀제곱합) / (전체변동량)으로 결정합니다.
위 값이 1에 가까울 때(ssr이 클 때) 좋은 모델이라고 할 수 있습니다.
회귀제곱합(SSR)이 낮다는 것은 (y^와 y¯) 의 차이가 작다는 것입니다.
이러면 굳이 회귀 모형(y^)을 사용하지 않고 평균 y값( y¯ )을 이용해도 되기에 좋은 모델이 아닙니다.
SST = SSE + SSR이기 때문에,모델의 성능은 1- (오차제곱합) / (전체변동량)으로도 결정합니다.
sse가 작을 때 좋은 모델이라고 할 수 있습니다.
오차제곱합(SSE)이 크다는 것은 (y와 y^) 의 차이가 크다는 것입니다.
두 변수의 연관성을 나타낸 회귀모형을 만들었는데, 실제 y값과 추정 y값의 차이가 크면 해당 모델의 신뢰성은
떨어집니다. 고로 좋은 모델이라고 할 수 없습니다.
모델은 SSR/SST가 1에 가까울 때 좋은 성능을 가진다.
회귀제곱합(SSR)이 커야 좋은 모델이다!
오차제곱합(SSE)가 작아야 좋은 모델이다!
다음에 ‘회귀 분석 실습’으로 찾아 뵙겠습니다!
