Singular Value Decomposition(SVD, 특이값 분해)은 행렬을 분해하는 기법이다.
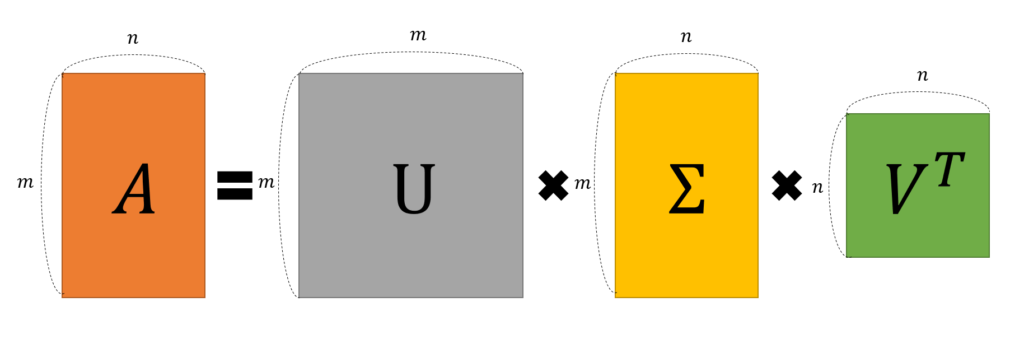
A(mxn)라는 행렬이 있을 때, A=USVT로 분해되며, U,S,V는 다음을 만족하는 행렬이다.
U: orthogonal matrix (직교 행렬: UT=U-1이며 UUT=I를 만족함)
크기는 항상 mxm이며, left singular vector라고 불리는 u를 열벡터로 가진다.
ex) U = [u1 | u2 | u3 | ,…., | um]
S: diagonal matrix (대각 행렬: S=ST이며 SST=S2을 만족함)
크기는 항상 mxn이며, singular value라고 불리는 σ를 주대각원소로 가진다.
m>n인 경우, singular value는 n개를 지니며 행렬의 아랫공간에 0이 배치된다.
m=n인 경우, singular value는 m개를 지니며 정방행렬이다.
m<n인 경우, singular value는 m개를 지니며 행렬의 옆공간에 0이 배치된다.
V: orthogonal matrix (직교 행렬: VT=V-1이며 VVT=I를 만족함)
크기는 항상 nxn이며, right singular vector라고 불리는 v를 열벡터로 가진다.
ex) V = [v1 | v2 | v3 | ,…., | vn]
먼저 V는 ATA의 고유벡터를 열벡터로 가지는 직교행렬이다.
이는 Eigen Decomposition(고유값 분해)을 통해 알 수 있다.
ATA는 항상 symmetric matirix(대칭 행렬)이므로 diagonalizable(대각화 가능)한 특징이 있어 고유값 분해가 가능하다. 즉 ATA=VΛV-1로 분해가 가능하다. (V는 고유벡터로 이루어진 행렬, Λ는 고유값으로 이루어진 대각행렬)
또한 symmetric한 특징에 의해 V는 직교행렬이 되어 ATA=VΛVT로 분해가 가능하다.
그런데 A=USVT식에 따라 ATA는 (VSTUT)(USVT)=VSTSVT로 정리된다.
따라서 ATA=VΛVT=VSTSVT이므로, V는 ATA의 고유벡터로 이루어진 행렬이다.
또한 S는 ATA행렬의 고유값에 루트를 취한 값으로 이루어진 대각행렬이다.
이는 ATA의 Eigen Value를 구하는 과정에서 확인이 가능하다.
det(ATA-λI)=0을 만족하는 λ를 찾으려고 할 때,
det(ATA-λI)=det(VSTSVT-λI)가 되고 이 식은 아래와 같이 정리할 수 있다.
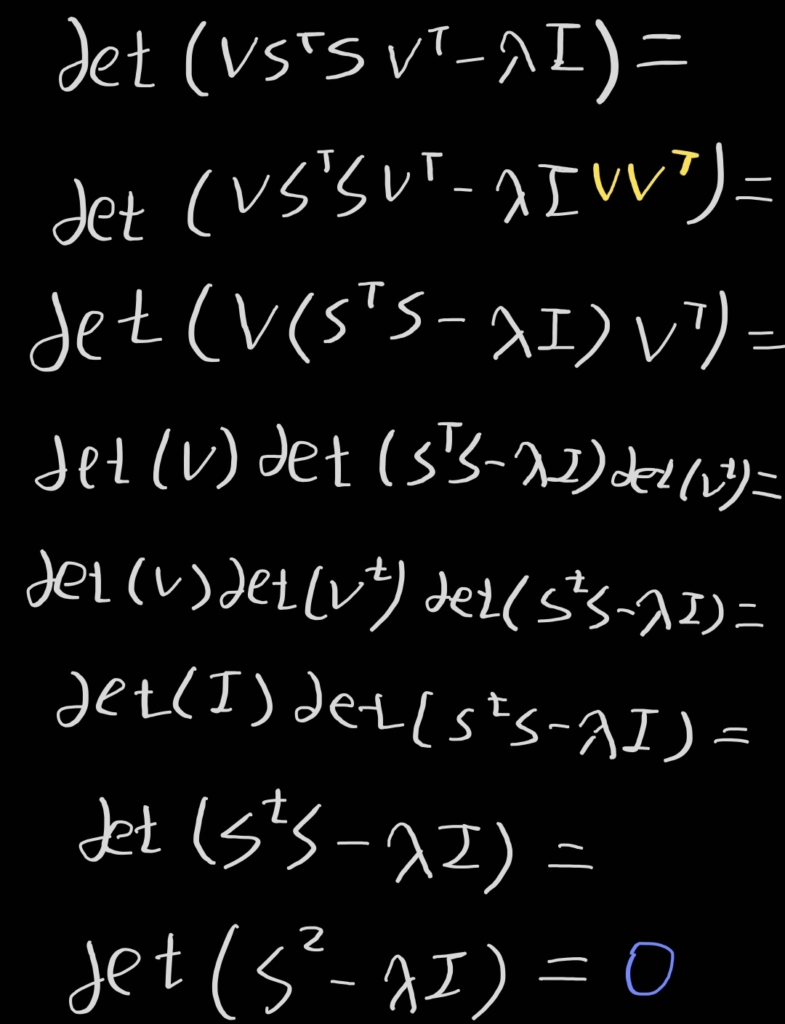
여기서 행렬 S2-λI는 (σ12-λ, σ22-λ, σ32-λ, …, σn2-λ)을 주대각 원소로 가지는 대각 행렬이므로, σ=square root(λ)일 때 행렬식이 0이 된다.
마지막으로 U는 Av=σu를 만족하는 u를 열벡터로 가지는 직교행렬이다.
이는 A=USVT식에 V를 곱하면 확인이 가능하다.
AV=USVTV이므로 AV=US이고, 다음을 만족한다.
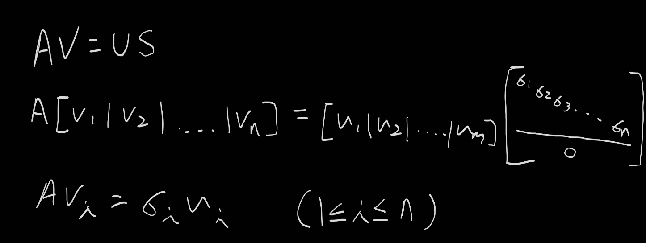
따라서 V(v1,v2,..,vn)와 S(σ1,σ2,…,σn)를 구했다면, U(u1,u2,…,um)는 ui=1/σi * Avi에 대입해서 계산하면 된다.
P.s. U는 AAT의 고유벡터를 열벡터로 가지는 직교행렬이기도 하다, S는 AAT의 고유값을 주대각원소로 지니는 행렬이기도 하다.
지금까지 증명한 내용을 정리하면 SVD는 다음 세 단계로 해결이 가능하다!
1. S 행렬을 구하기 위해, σ는 ATA행렬의 고유값에 루트를 씌워서 계산한다.
2. V 행렬을 구하기 위해, v는 ATA행렬의 고유벡터를 계산한다.
3. U 행렬을 구하기 위해, u는 Av=σu를 이용해서 계산한다.
이제 연습 문제를 한 번 풀어보겠다.
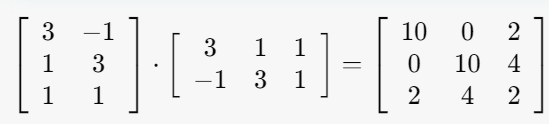
Q. A=[3,1,1; -1,3,1]일 때, SVD로 행렬을 분해하시오.
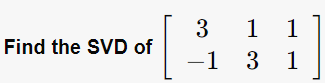
0. Shape 추정
U: mxn = 2×2
S: mxm = 2×3 (singular value는 2개)
V: nxn = 3×3
1. σ를 ATA의 eigen-value로 구하기
det(ATA-λI)=0을 만족하는 λ구하고 square root 취하기!
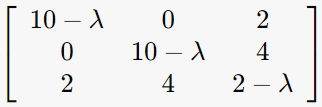
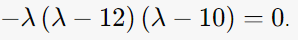
λ = 12, 10, 0
-> σ = 2√3, √10 (singular value는 2개)
S = 2√3, √10을 대각원소로 지님
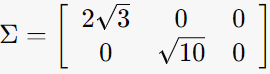
2. ATA의 eigen-vector로 V구하기
(ATA-λI)*v=0을 만족하는 v구하기
2-1. λ=12인 경우

2-2. λ=10인 경우
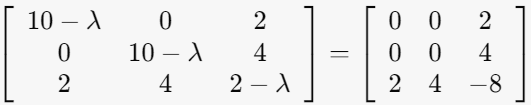
2-3. λ=0인 경우
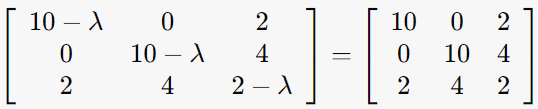
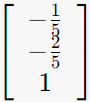
V = (unit vector v1 | unit vector v2 | unit vector v3)
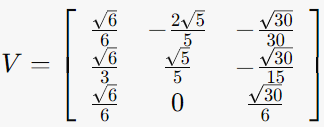
3. Av=σu를 만족하는 u구하기
u=1/σ * Av에 해당하는 u구하기
3-1. σ1=2√3, v1= (√6/6, √6/3, √6/6)인 경우
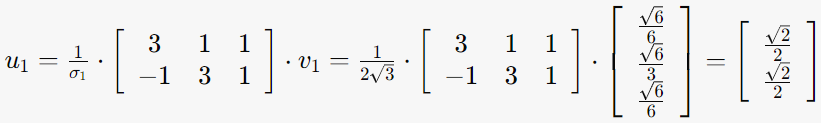
3-2. σ2=√10, v2= (–2√5/5, √5/5, 0)인 경우
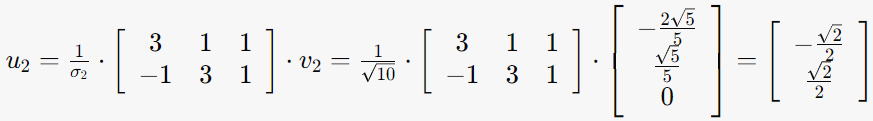
3-3. σ3=0, v3= (-√30/30, -√30/15, √30/6)인 경우
-> σ가 0이므로 계산 불가
U = (u1 | u2)
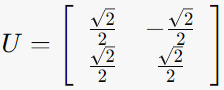
파이썬을 이용한 SVD 계산은 Python Code를 통해 참고하길 바란다.
SVD 활용
SVD는 영상처리에서 이미지 압축을 하는 용도로 많이 사용된다.
바로 Truncated SVD를 이용하는 개념이다.

Truncated SVD란 일부 Singular Value를 이용해서 행렬 A를 재구축하는 방식이다.
즉 U(mxm) * S(mxn) * VT(nxn)을 통해 A(mxn)를 재구축하는 것을 Full SVD라고 한다면,
Ur(mxr) * Sr(rxr) * VrT(rxn)을 통해 A(mxn)를 재구축하는 것은 Truncated SVD라고 한다.
Singular Value 전체를 이용하면 행렬 A와 똑같은 행렬로 재구축이 되지만, 일부만을 이용하면 A와 유사하지만 정보량이 감소한 행렬로 재구축이 된다.
영상처리에서 이미지는 행렬로 생각할 수 있기 때문에, Truncated SVD를 적용해서 정보량이 감소한 이미지로 재구축을 하면 이미지 압축을 했다고 표현한다.
이 내용에 대한 예제는 Python Code를 참고하길 바란다.
PCA와의 관계
PCA(주성분 분석): 차원 축소를 할 때 사용하는 알고리즘이다. 예를 들어 데이터가 2차원상에 점들로 흩어져 있고, 이 점들을 1차원 공간에 매핑하고 싶다면 각 축에 대응되도록 점을 이동시키는 방법이 가장 간단한 방법일 것이다. 그런데 이렇게 하면 점들이 겹쳐서 정보의 유실이 발생한다. 따라서 점들의 분산을 최대화하는 축을 찾아야 되는데, 이 축을 구하는 방법이 PCA이다. PCA에 따르면, 공분산 행렬의 고유값 중 가장 큰 값에 대응되는 고유벡터가 분산을 최대화하는 축에 해당이 된다. 이 축으로 데이터를 정사영 내림으로써 차원 축소를 하는 방법이다.
X~를 [x1-µ, x2-µ, …, xn-µ]인 열벡터들로 이루어진 행렬이라고 할 때,
공분산의 수식은 1/n * X~ * X~T가 된다.
결국 X~ * X~T의 가장 큰 고유값에 대응되는 고유벡터가 필요한 것인데,
이것은 X~의 SVD로 구한 U의 1행을 구하는 것과 같다.
따라서 PCA 문제를 풀 때는
SVD 문제로 대치해서 풀어도 된다!
