DLFS – Backpropagation

By MasterData Science, Machine Learning

※ Deep Learning From Scratch (밑바닥부터 시작하는 딥러닝)에 대한 정리 자료입니다.

Backpropagation(역전파)이란 Chain Rule을 이용해서 미분을 빠르게 계산하는 방법을 의미한다.

Chain Rule(연쇄법칙)은 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다는 법칙이다. 예를 들어, z=t2이고 t=x+y일 때 ∂z/∂x=(∂z/∂t)*(∂t/∂x)=2t*1=2(x+y)로 계산할 수 있다.

딥 러닝에서 학습이란 손실함수(Loss)를 최소화시키는 가중치(W)와 편향(b)을 찾는 것이고,
이 과정에서 W와 b의 기울기(Gradient)를 알아야 된다.

수치미분(Numerical Differentiation)을 이용해서 모든 W와 b에 대한 Gradient를 구할 수도 있지만, 이는 매우 느린 방법으로 실제로 사용되기가 어렵다. 반면 Backpropagation을 이용하면 전체 함수를 합성 함수로 생각함으로써 Gradient 계산 시 수식이 더욱 간단해지고 훨씬 빠른 연산 속도를 보인다.
ex) y=XW+b를 y=z+b, z=XW로 이루어진 합성 함수로 생각함

따라서 Backpropagation을 이용해서 Gradient를 찾고, 경사하강법(Gradient Descending)으로 W와 b를 업데이트하는 방법으로 학습을 진행한다.

지금부터는 딥러닝에 필요한 Backpropagation 과정을 차례차례 살펴보겠다.


ReLU의 Backpropagatiopn

ReLU의 수식은 다음과 같다.

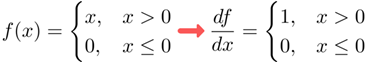
x가 0초과인 경우에 해당하는 계산 그래프를 표현하겠다.

ReLU 뒤에 Loss(손실 함수)가 있다고 가정하고 Backpropagation을 한 것이다.
왜냐하면 딥러닝에서 학습을 할 때는 L(손실 함수 값)이 얼마나 변하는가에 집중하기 때문이다.
ex) ∂L/∂w: w가 변할 때 L이 얼마나 변하는가

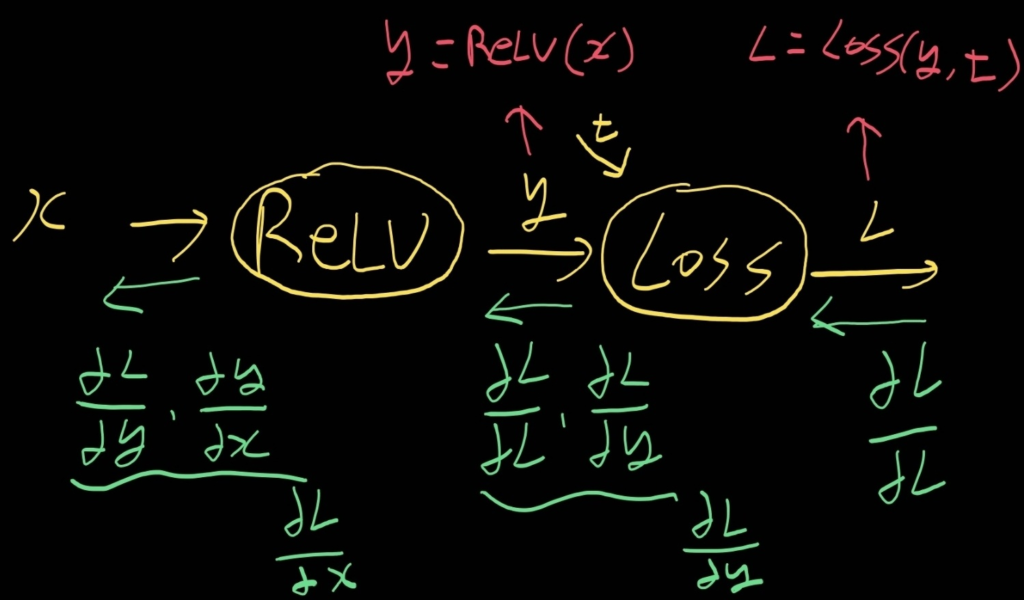
먼저 ∂L/∂y는 ∂L/∂L*∂L/∂y이므로 1*∂L/∂y가 된다.
이후에 ∂L/∂x는 ∂L/∂y*∂y/∂x이고 y=x이므로, ∂L/∂y*1이 된다.

다음은 x가 0이하인 경우이다.

∂L/∂x는 ∂L/∂y*∂y/∂x이고 y=0이므로, ∂L/∂y*0 = 0이 된다.

이제 ReLU함수에서 ∂L/∂x가 무엇인지 알았으니 이를 코드로 표현하겠다.
코드에서 out은 y에 해당한다.

class ReLU:
    def __init__(self):
        self.mask=None
        
    def forward(self,x):
        self.mask=(x<=0)
        out=x.copy()
        out[self.mask]=0
        return out
    
    # dout=∂L/∂out
    def backward(self,dout):
        # x<=0이면 0, 아니면 dout
        dout[self.mask]=0
        dx=dout # dx=∂L/∂x
        return dx


Sigmoid의 Backpropagation

Sigmoid의 수식은 다음과 같다.

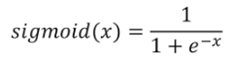
Sigmoid를 합성함수로 표현하는 계산 그래프는 다음과 같다.

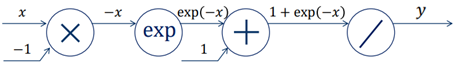
계산 그래프에서 앞으로 가는 방향은 Forward라 하고 뒤로 가는 방향은 Backward라고 한다.
Backward에 해당하는 값인 변화량을 차근차근 계산해보겠다.

그 전에 이해를 돕기 위해 계산 그래프를 다시 표현하겠다.

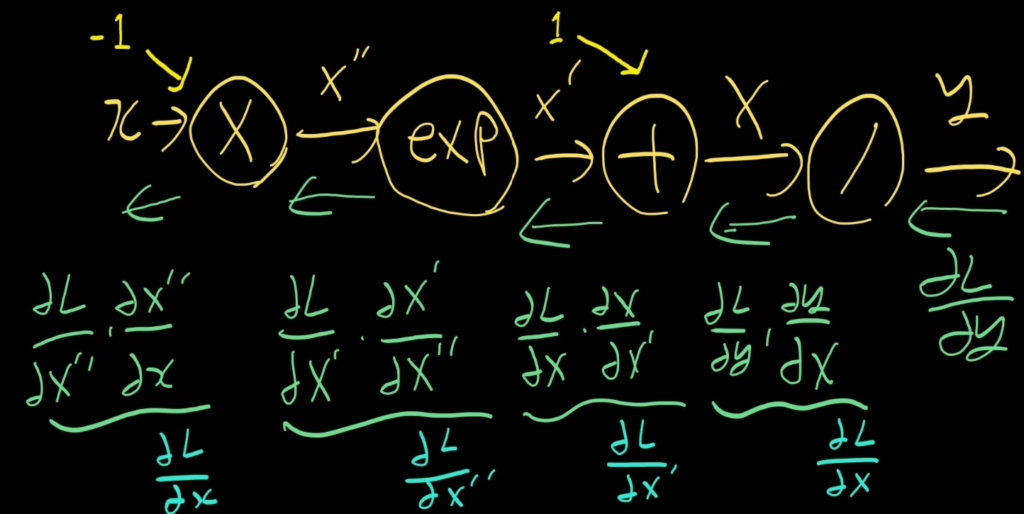
1. y의 변화량 (∂L/∂y)
sigmoid를 거친 후 Loss까지 고려하면, ∂L/∂y가 된다.
무슨 Loss가 사용할지 모르니 이렇게 표현한 것이다.

2. X=1+exp(-x)의 변화량 (∂L/∂X)
y=1/X라고 표현할 때, ∂L/∂X = ∂L/∂y * ∂y/∂X = ∂L/∂y * (-1/X2)이다.
이 식에서 (1/X2)는 y2과 같으므로, -∂L/∂y * y2이 된다.

3. X’=exp(-x)의 변화량 (∂L/∂X’)
X=X’+1이라고 표현할 때, 더하기에 대한 Backpropagation은 그대로이다.
따라서 -∂L/∂y * y2이 된다.

4. X”=-x의 변화량 (∂L/∂X”)
X’=ex’’이라고 표현할 때, ∂L/∂X” = ∂L/∂X’ * ∂X’/∂X” = (-∂L/∂y * y2) * ex’’이다.
이 식에서 ex’’은 e-x와 같으므로, -∂L/∂y * y2 * e-x가 된다.

5. x의 변화량 (∂L/∂x)
X”=x*-1이라고 표현할 때, 곱하기에 대한 Backpropagation은 이전에 구한 변화량(∂L/∂X”)에 상대(-1)를 곱한 값이다. 따라서 ∂L/∂y * y2 * e-x이 된다.
이 식은 다음과 같이 정리가 가능하다.

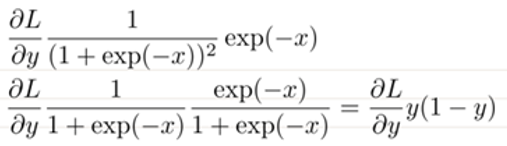
이제 Sigmoid함수에서 ∂L/∂x가 무엇인지 알았으니 이를 코드로 표현하겠다.
코드에서 out은 y에 해당한다.

class sigmoid:
    def __init__(self):
        self.out=None
    
    def forward(self,x):
        out=1/(1+np.exp(-x))
        self.out=out
        return out

    # dout=∂L/∂out
    def backward(self,dout):
        dx=dout*self.out*(1-self.out)
        return dx


Affine의 Backpropagation

Affine의 계산그래프는 다음과 같다.

Z=X*W라고 표현할 때, ∂L/∂X = ∂L/∂Z * ∂Z/∂X가 된다.
여기서 ∂L/∂Z는 더하기에 대한 Backpropagation이므로 ∂L/∂Y와 같다.
∂Z/∂X는 행렬에 대한 Backpropagation이고, 이 때는 상대(W)를 전치한 뒤 곱한 값과 같다.
따라서 ∂L/∂Y * WT가 된다.

이와 같은 계산을 통해, 계산그래프를 Backward까지 표현하면 다음과 같다.

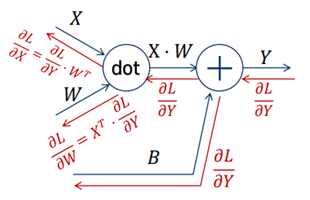
이제 Sigmoid함수에서 ∂L/∂X가 무엇인지 알았으니 이를 코드로 표현하겠다.
코드에서 out은 y에 해당한다.

class Affine:
    def __init__(self,W,B):
        self.W=W # ex) 2x3
        self.B=B # ex) 1x3
        self.X=None
        self.dW=None
        self.db=None
    
    # ex) X: 1x2
    def forward(self,X):
        self.X=X
        out=np.dot(X,self.W)+self.B
        return out
    
    # dB = dL/dy -- dout 
    # dX = dL/dy * W^T
    # dW = dL/dy * X^T
    def backward(self,dout):
        dX=np.dot(dout,self.W.T)
        self.dW=np.dot(self.X.T,dout)
        self.dB=np.sum(dout,axis=0)
        return dX


SoftmaxWithLoss의 Backpropagation

Softmax의 계산그래프는 다음과 같다.
n은 3으로 가정하였다.

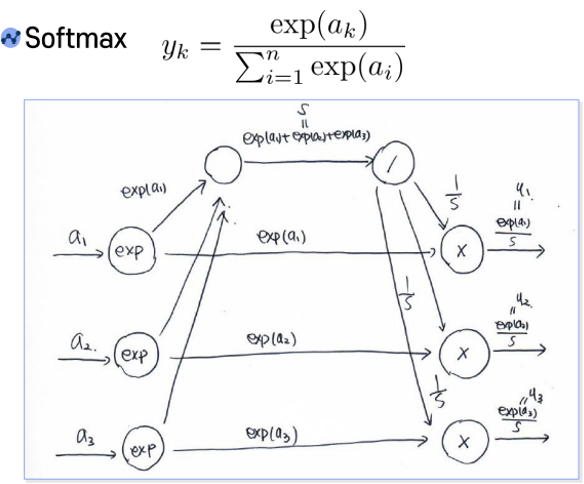
Loss를 Cross Entropy를 채택할 때, 계산 그래프는 다음과 같다.
k는 3으로 가정하였다.

Cross Entropy에 대한 Backward는 다음과 같다.

Softmax에 대한 Backward는 다음과 같다.

  1. Softmax이후 CrossEntropy를 진행하므로, exp(ai)/s는 yi로 표현할 수 있다.
  2. 곱하기에 대한 Backpropagation은 이전에 구한 변화량에 상대를 곱한 값이다.
    -> ∂L/∂(1/s) = (-t1/y1) * exp(a1), (-t2/y2) * exp(a2), (-t3/y3) * exp(a3)
  3. 1/yi는 s/exp(ai)이므로 식을 정리하면 ∂L/∂(1/s) = -t1s, -t2s, -t3s이다.
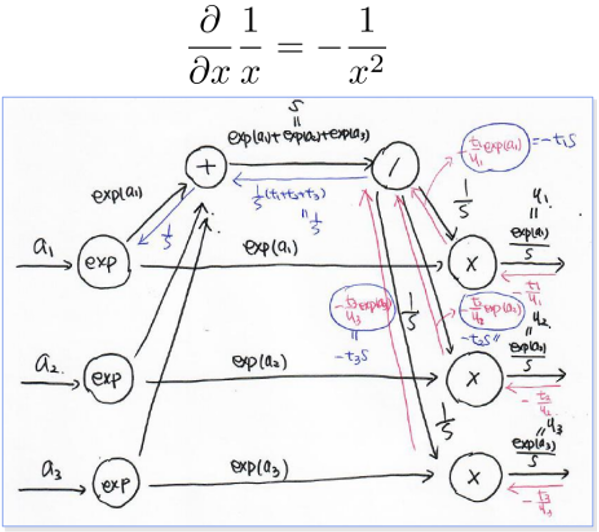
  1. s’=1/s라고 생각할 때, ∂L/∂s’은 (-t1s, -t2s, -t3s)이다.
  2. ∂L/∂s = ∂L/∂s’ * ∂s’/∂s이 성립하고, ∂s’/∂s는 -1/s2이다.
  3. ∂L/∂s = (-t1s, -t2s, -t3s) * (-1/s2)이므로 (t1/s, t2/s, t3/s)가 된다.
    그런데 forward를 할 때 여러 방향으로 퍼지는 경우, Backward를 할 때는 변화량을 모두 더해서 표현한다. 따라서 (t1+t2+t3)/s가 된다.
  4. (t1+t2+t3)/s는 1/s과 같다. 왜냐하면 t는 원핫벡터이므로 ti의 합이 1이 되기 때문이다.
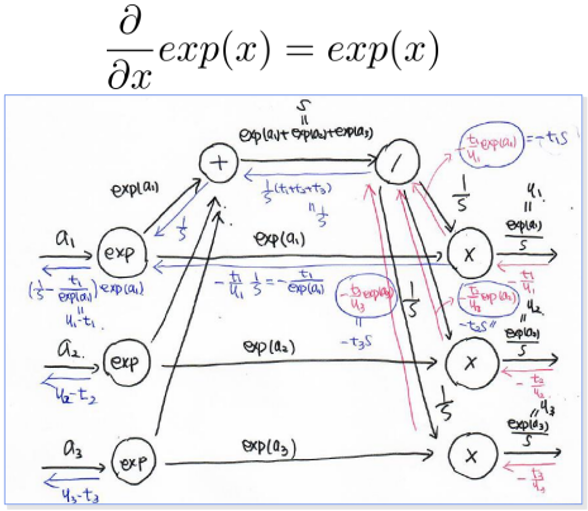
  1. 곱하기에 대한 Backpropagation은 이전에 구한 변화량에 상대를 곱한 값이다.
    -> ∂L/∂(exp(ai)) = (-t1/y1) * (1/s)
  2. 1/yi는 s/exp(ai)이므로 식을 정리하면 ∂L/∂(exp(ai)) = -ti/exp(ai)이다.
  3. ai‘=exp(ai)라고 생각할 때, ∂L/∂ai‘은 [1/s, -ti/exp(ai)]이다.
  4. ∂L/∂ai = ∂L/∂ai‘ * ∂ai‘/∂ai이 성립하고,∂ai‘/∂ai는 exp(ai)이다.
  5. ∂L/∂ai는 [1/s, -ti/exp(ai)] * exp(ai)이므로 [exp(ai)/s, -ti]이 된다.
    forward를 할 때 여러방향으로 퍼졌으므로, exp(ai)/s -ti = yi-ti 즉 오차가 된다.

SoftmaxWithLoss를 요약하면 다음과 같다.

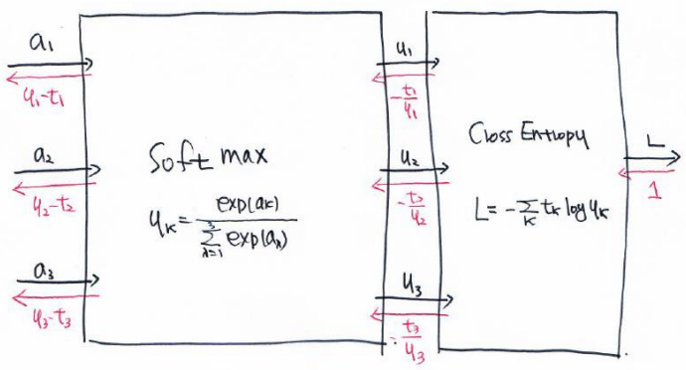
SoftmaxWithLoss의 ∂L/∂ai가 무엇인지 알았으니 이를 코드로 표현하겠다.
코드에서 out은 L에 해당하며, 배치 사이즈까지 고려하였다.

# yk = exp(ak) / ∑(i=1 to n)(exp(ai))
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)  # 오버플로 대책
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

def cross_entropy_error(y, t):
    delta = 1e-7  # 0일때 -무한대가 되지 않기 위해 작은 값을 더함
    return -np.sum(t * np.log(y + delta))

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None  # 손실
        self.y = None     # softmax의 출력
        self.t = None     # 정답 레이블(원-핫 벡터)

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)  
        self.loss = cross_entropy_error(self.y, self.t)

        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = self.y - self.t / batch_size

        return dx


Backpropagation을 이용해서 (w1,b1,w2,b2)에 대한 Gradient구하기

class TwoLayerNet:
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        self.params={}
        # input_size * hidden_size
        self.params['W1']=weight_init_std*np.random.randn(input_size,hidden_size)
        # 1 * hidden_size
        self.params['b1']=np.zeros(hidden_size)
        # hidden_size * output_size
        self.params['W2']=weight_init_std*np.random.randn(hidden_size,output_size)
        # 1 * output_size
        self.params['b2']=np.zeros(output_size)
        
        # layer 구성
        # OrderDict: 순서를 바꿀 수 없는 딕셔너리 
        self.layers=OrderDict()
        self.layers['Affine1']=Affine(self.params['W1'],self.params['b1'])
        self.layers['Relu1']=Relu()
        self.layers['Affine2']=Affine(self.params['W2'],self.params['b2'])
        self.lastLayer=SoftmaxWithLoss()
        
    def predict(self,x):
        for layer in self.layers.values():
            x=layer.forward(x)
        return out
        
    def loss(self,x,t):
        y=self.predict(x)
        return self.lastLayer.forward(y,t)
        
    def gradient(self,x,t):
        self.loss(x,t)
        dout=1
        dout=self.lastLayer.backward(dout)
        layers=list(self.layers.values(0))
        layers.reverse()
        for layer in layers:
            dout=layer.backward(dout)
        grads={}
        grads['W1']=self.layers['Affine1'].dW
        grads['b1']=self.layers['Affine1'].db
        grads['W2']=self.layers['Affine2'].dW
        grads['b2']=self.layers['Affine2'].db
        return grads

Leave a Reply

Your email address will not be published. Required fields are marked *