클러스터링: 비슷한 데이터끼리 클러스터(그룹)를 만드는 것! , 군집화라고도 부름
클러스터링 예시
고객 세분화
: 은행에서 일일히 한명한명 맞춤화된 서비스를 제공할 수는 없으므로 (나이or성별 등) 으로 클러스터를 구성하여 맞춤화된 서비스를 제공함!
클러스터의 특징!
같은 그룹에 속하는 아이템들은 서로 비슷하고, 그 외의 아이템은 아주 달라야 한다.
즉 그룹을 구성하기 전 (비슷하다와 다르다)를 객관화할 수 있어야 한다.!
비슷하다는 것을 컴퓨터에게 어떻게 알려줘야 하는지 알아 봅시다!
유클리드 거리 공식(최단거리를 쟤는 기법)을 사용합니다!
가까운 데이터는 비슷하다고 취급하는 것입니다!
[ 유사도 측정에는 유클리드 거리 공식!! ]
P와 Q사이의 거리
Dist(p,q) = { Sigma(i=1 -> n) (pi-qi)^2 } ^(1/2)
n: p,q의 좌표 개수
ex) P(3,0), Q(2,1)
=> { (3-2)^2 + (0-1)^2 }^(1/2) = √ 2
유클리드 거리 공식을 이용해서 그룹을 만드는 알고리즘을 알아 봅시다!
K-means 알고리즘
: k개의 그룹으로 데이터를 나누는데, 아이템들의 평균값을 이용하여 센터(대표)를 잡고 그 센터와 비슷한 (가까운) 아이템들만 같은 그룹에 넣음
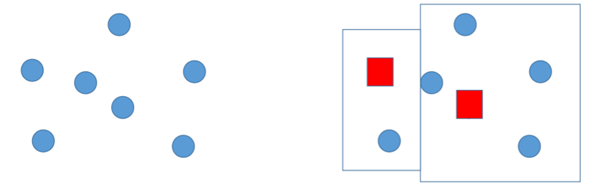
1. 원소 중에 임의로 센터<임시 대표>를 정함 (임시 대표 개수:2개) / 빨간 사각형이 임시 대표
2. 임시 대표와 가까운 아이템을 그룹으로 정함 <그룹 2개 생성 > / 유클리드 공식 적용
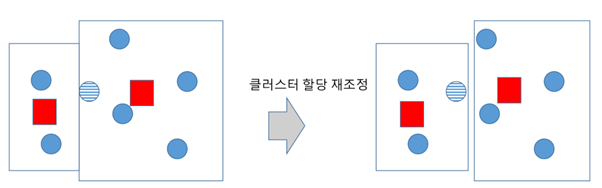
3. (그룹 간 원소의) 거리 평균값을 이용해서 센터(대표)를 다시 지정함 / 왼쪽 이미지
4. 센터가 다시 지정됐으니 그룹에 있는 아이템이 대표와 멀어짐 / 왼쪽 이미지 – 빗금 친 원소
=> 대표와 가까운 아이템으로 다시 그룹을 정함 <그룹 조정> / 오른쪽 이미지

5. (그룹 간 원소의)평균값을 이용해서 센터(대표)를 다시 지정함
6. 대표와 가까운 아이템으로 다시 그룹을 정하려 했는데, 오른쪽 사진과 같이 그럴 필요가 없음
[그룹에 있는 아이템들이 이미 바뀐 대표와 가까이 있음]
7. 알고리즘 종료
[ 랜덤으로 센터 지정 -> (유클리드로 그룹 지정 -> 평균값으로 센터 지정) 반복 -> 유클리드를 써도 크게 차이가 없는 경우가 생김 -> 종료 ]
이번에는 클러스터의 개수로 클러스터의 두 번째 특징을 알아 봅시다!
비슷한 데이터로 묶인 A라는 한 그룹이 있었습니다.
이 그룹을 반으로 쪼개서 A1, A2그룹으로 만들면 어떻게 될까요?
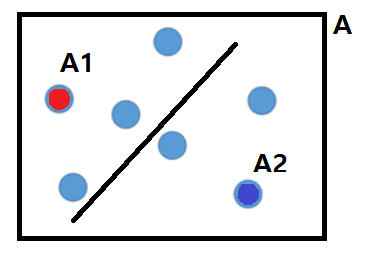
이질성은 데이터간 거리가 멀수록 커지게 됩니다.
A1 그룹과 A2 그룹 데이터가 비슷하다보니(가까우니), 그룹 간 이질성은 크지 않게 됩니다!
=> 그룹 수를 높이면 그룹 간 이질성은 떨어진다.
유사성은 데이터간 거리가 가까울 수록 커지게 됩니다.
기존 A그룹에 있는 원소 간 거리랑 A1 그룹의 원소 간 거리를 비교하면 어떻게 될까요?
A는 (빨간 원소)와 (파란 원소)도 고려해서 거리를 구해야 하지만 A1은 그럴 일이 없습니다.
결국 그룹 내 유사성은 커지게 됩니다!
=> 그룹 수를 높이면 그룹 내 유사성은 늘어난다.
그룹 수를 높이면 그룹 간 이질성은 줄어들고, 그룹 내 유사성은 커진다!
그룹 수를 줄이면 그룹 간 이질성은 커지고, 그룹 내 유사성은 줄어든다!
위 특징을 살펴 보면 (클러스터의 개수는 너무 많아도 적어도 좋지 않다!) 라는 결론이 나오게 되네요!
이를 R 프로그래밍으로 확인해봅시다!
iris iris[,1:4] # iris데이터의 1열~4열만 가져와서 3개로 군집 irisCluster<-kmeans(iris[,1:4],3) irisCluster # 150개의 데이터를 어떻게 세 그룹으로 나눴는지 차례대로 나타냄 # 군집화된 데이터들을 보여줌 irisCluster$cluster # 군집화된 데이터들이 어떤 종에 해당하는지 수를 보여줌 table(irisCluster$cluster,iris$Species)
결과)
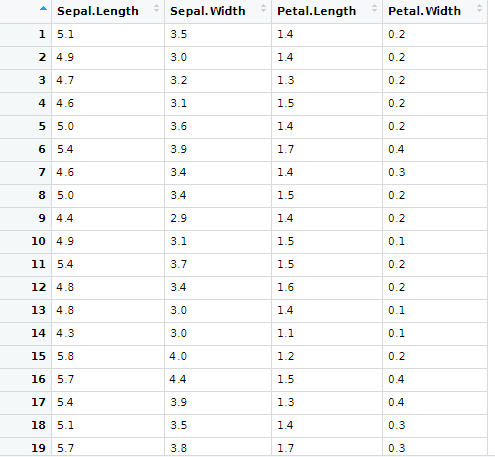
위는 iris(꽃) 데이터의 1열부터 4열까지를 나타낸 것입니다.
각 꽃마다 꽃받침(sepal),꽃잎(petal)의 길이 너비를 나열하였습니다.
이러한 데이터가 있으면 길이와 너비가 비슷한 것끼리 묶으면 꽃들을 클러스터링 할 수 있습니다!
ex) [1](5.1 , 3.5, 1.4, 0.2) [2] (4.9, 3.0, 1.4, 0.2) [3] (4.7 3.2 1.3 0.2)… 데이터를 4차원 공간 상에 놓고,
[ 랜덤으로 센터 지정 -> (유클리드로 그룹 지정 -> 평균값으로 센터 지정) 반복 -> 유클리드를 써도 크게 차이가 없는 경우가 생김 -> 종료 ]
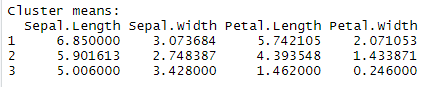
kmeans(iris[,1:4],3)을 통해 3개의 클러스터를 만들었습니다.
첫 번째 클러스터는 꽃받침 길이 평균은 6.8 , 꽃받침 너비 평균은 3.07, 꽃잎 길이는 5.7, 꽃 잎 너비는 2.07
이렇게 클러스터링 되었네요!
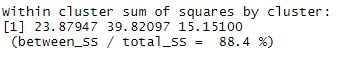
위는 각 그룹 내 일반화된 아이템 간 거리를 나타낸 것입니다.
[ 일반화된 아이템 간 거리 계산: 아이템을 두 개씩 묶어서 간격을 구하고 이들을 다 합쳐서 루트씌운 값 ]
이렇게 보면 두 번째 그룹 내 아이템 간 거리가 가장 크고, 유사성이 가장 작습니다.
표를 통해 정말 그런지 확인해봅시다!

첫 번째 그룹은 그룹 내 유사성이 중간이고 virginica데이터를 주로 갖습니다.
두 번째 그룹은 유사성이 가장 작으니 versicolor데이터와 virginica데이터를 많이 가지게 됩니다.
세 번째 그룹은 유사성이 가장 크고 setosa데이터만 가지게 됩니다.
다음에는’클러스터링 실습’으로 찾아 뵙겠습니다!
