‘의사결정나무’를 모르시겠다면 이전 포스팅 글을 참고하세요!!
-> https://shacoding.com/2019/09/20/mining-%ec%97%94%ed%8a%b8%eb%a1%9c%ed%94%bc%ec%99%80-%ec%a7%80%eb%8b%88%ec%a7%80%ec%88%98/

지니지수
무질서도를 나타내는 척도입니다.
엔트로피와 마찬가지로, 두 비율이 0.5로 가까워질 때 값이 제일 커집니다.

공식은 아래와 같습니다.

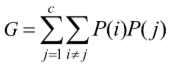
안쪽 시그마부터 알아 봅시다.

P(j)를 클래스A, 나머지 클래스들 P(i)가 존재한다고 생각합시다.
클래스A를 중심으로 A를 제외한 나머지 클래스와 한 번씩 곱하고 더합니다.

j=1 -> P(1)이 중심이면
P(1)*p(2) + p(1)*p(3) + p(1)*p(4) + …이 됩니다!

P(1)*{ p(2)+p(3)+p(4)+… }
-> 나머지 클래스들을 다 더한 것은 [ 전체-p(1) ]과 같습니다.

j=1일 때 P(1)*(1-p(1)) 이니까,
결국 안쪽 시그마는 P(j)*(1-p(j)) 로 정리가 됩니다!

이제 바깥쪽 시그마를 알아 봅시다!

Sigma(j=1->c) P(j)*(1-p(j))
(=) Sigma(j=1->c) P(j)- Sigma(j=1->c) p(j)^2

Sigma(j=1->c) P(j)는 어차피 1이므로,
1-Sigma(j=1->c) p(j)^2가 됩니다.

G = 1- Sigma(j=1->c) P(j)^2
p(j)는 범주에 속하는 레코드 비율, c는 범주의 개수

이제 지니지수 공식도 알았으니 예시를 통해 문제를 풀어 봅시다!

분리하기 전에는 범주가 <신용 상태(나쁨)과 신용상태(좋음)> 두 가지입니다.
분리한 후에는 영역 <급여형태(주급)과 급여형태(월급)>이 추가 되었습니다.

분리하기 전부터 살펴 봅시다!
=> G=1-( (168/323)^2+(155/323)^2) )

분리한 후에는 엔트로피 구할 때와 비슷합니다.
Sigma(i=1->d) [ Ri * { 1- Sigma(j=1->c) P(j)^2 } ]
d: 영역의 개수

G주급 = 1-(143/165)^2-(22/165)^2
G월급 = 1-(25/158)^2-(133/158)^2
=> 165/323 * G주급 + 158/323 * G월급

이를 R 프로그래밍으로 확인해봅시다!

# 범주가 두 개일 때 지니지수 값 구하기 
Gini=function(pj){
  return (1- (pj^2 + (1-pj)^2) )
}

# 영역이 두 개일 때 분할 후 지니지수 값 구하기
Gini2=function(r1,pj1,pj2){
  # r1은 첫 번째 영역 레코드 비율
  # pj1은 첫 번째 영역에서 한 범주의 레코드 비율 
  # pj2은 두 번째 영역에서 한 범주의 레코드 비율 
  
  # pj1의 Gini
  one=Gini(pj1)
  # pj2의 Gini
  two=Gini(pj2)
  
  return(r1 * one + (1-r1) * two)
}

# 분할 전 지니지수 구하기!
Gini(168/323)

# 지니지수 함수로 (분할 후 지니지수) 풀기!
165/323 * Gini(143/165) + 158/323 * Gini(25/158)
# 지니지수2 함수로 (분할 후 지니지수) 풀기!
Gini2(165/323,143/165,25/158)

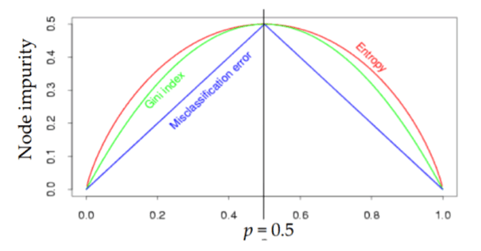
엔트로피와 비교해 봅시다!

지니지수: 0.49 -> 0.24
엔트로피: 0.99 -> 0.59

실제 무질서도 차이는 같지만,
엔트로피에 비해 지니지수가 수치 상 더 큰 차이를 가지네요!!

실제로 ‘의사결정나무’ 문제를 풀 때
(엔트로피) 혹은 (지니지수)를 이용한 알고리즘을 이용합니다.

알고리즘에 의해 분할을 계속해가며 정리하는데,
그 정리의 정도를 엔트로피나 지니지수로 확인하는 것이지요!

엔트로피지수를 이용하는 알고리즘은 C4.5이고
지니지수를 이용하는 알고리즘은 Cart입니다.

다음 포스팅에는 cart알고리즘을 사용해서 ‘의사결정나무 실습’ 을 해보겠습니다!