세그먼트 트리(Sement Tree)
특정 구간 내 데이터에 대한 연산을 빠르게 구할 수 있는 트리
(연산: 합, 최댓값, 최솟값 등)

세그먼트 트리의 잎 노드: 배열 원소와 같은 값
세그먼트 트리의 내부 노드: 구간(부분 배열)에 대한 값
세그먼트 트리의 높이: Ceil(O(log2N) (N은 배열의 크기)
세그먼트 트리의 크기: 2ceil(logn)+1-1 (log의 밑은 2)
(실제 코딩 시 index가 0인 원소는 사용하지 않으므로 트리 크기+1만큼 공간을 사용한다)
알고리즘
– 업데이트 (배열 원소 및 세그먼트 트리 수정)
– 구간 연산 (합, 최댓값, 최솟값 등)
시간복잡도
– 세그먼트 트리 생성: O(N)
– 업데이트: O(logN)
– 구간 연산: O(logN)
-> 데이터를 M번 업데이트 및 구간 연산: O(MlogN)

세그먼트 트리 (구간 합 구하기: Range Sum Query)
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int size;
int* s_tree;
int init(int* arr, int node, int s, int e) {
if (s == e)
return s_tree[node] = arr[s];
int m = (s + e) / 2;
// 재귀적으로 두 구간으로 나눈 뒤 그 합을 자기 자신으로 함
// ex) [node,s,e]=[1,0,4]=[2,0,2]+[3,3,4]
return s_tree[node] = init(arr, node * 2, s, m) + init(arr, node * 2 + 1, m + 1, e);
}
// s,e: 배열의 시작,끝 인덱스 (탐색하는 구간)
// l,r: 부분 배열의 시작,끝 인덱스 (합을 구하려는 구간)
int sum(int node, int s, int e, int l, int r) {
// case1) 탐색하는 구간이 부분 배열 구간과 무관 -> 0 리턴
// ex) s,e=(0,1), l,r=(2,3)
if (l > e || r < s)
return 0;
// case2) 탐색하는 구간이 부분 배열 구간에 속함 -> 노드의 값 리턴
// ex) s,e=(2,2), l,r=(2,3)
if (l <= s && e <= r)
return s_tree[node];
// 재귀적으로 두 구간으로 나눈 뒤 case2를 만족한 구간들을 합침
// ex) (l=2,r=3) -> (s=2,e=2)+(s=3,e=3)
int m = (s + e) / 2;
return sum(node * 2, s, m, l, r) + sum(node * 2 + 1, m + 1, e, l, r);
}
// s,e: 배열의 시작,끝 인덱스 (탐색하는 구간)
// idx: 배열의 특정 인덱스 (바꾸려는 원소)
// diff: idx번째 원소를 val로 변경할 때 기존 값과의 차이
void _update(int node, int s, int e, int idx, int diff) {
// 탐색하는 구간이 바꾸려는 원소를 지님
if (s <= idx && idx <= e) {
// 탐색하는 구간이 바꾸려는 원소와 일치 -> 종료
if (s == e) {
s_tree[node] += diff;
return;
}
else {
s_tree[node] += diff;
int m = (s + e) / 2;
// 재귀적으로 두 구간으로 나눈 뒤 idx와 관련있는 구간이면 업데이트
_update(node * 2, s, m, idx, diff);
_update(node * 2 + 1, m + 1, e, idx, diff);
}
}
// 탐색하는 구간이 바꾸려는 원소와 무관
return ;
}
void update(int node, int s, int e, int* arr, int idx, int val) {
int diff = val - arr[idx];
arr[idx] = val;
_update(node, s, e, idx, diff);
}
// 배열 출력
void aprint(int* arr, int size) {
printf("배열: ");
for (int i = 0; i < size; i++) {
printf("[%d] %d ", i, arr[i]);
}
printf("\n");
}
// 세그먼트 트리 출력
void sprint(int size) {
printf("세그먼트 트리: ");
for (int i = 1; i < size; i++) {
printf("[%d] %d ", i, s_tree[i]);
}
printf("\n");
}
int main(void)
{
// 배열 선언 및 배열 크기(size) 초기화
int arr[] = { 0,1,2,3,4,5 };
size = 6;
// 세그먼트 트리 선언
int h = (int)ceil(log2(size));
int tree_size = (int)pow(2, h + 1);
s_tree = (int*)calloc(tree_size, sizeof(int));
// 세그먼트 트리 초기화 (arr 배열 이용)
init(arr, 1, 0, size - 1);
// 배열 및 세그먼트 트리 출력
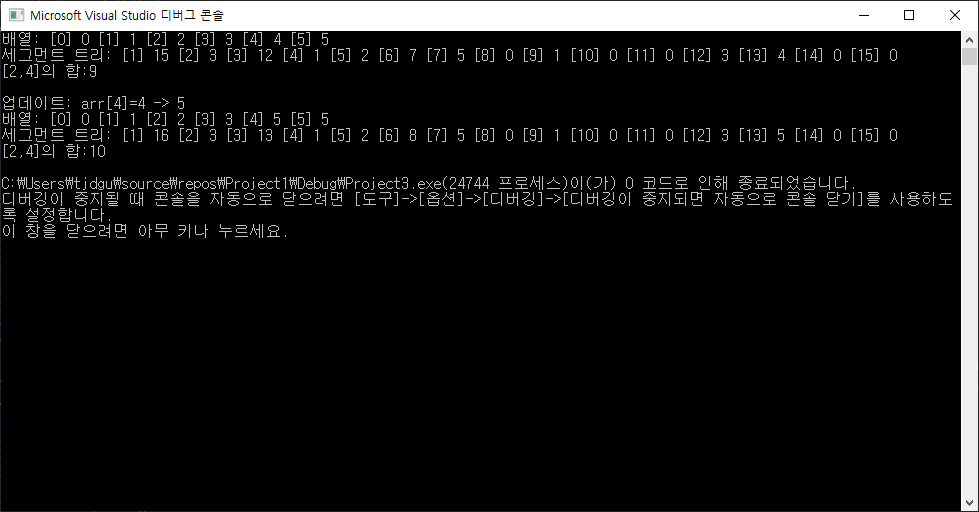
aprint(arr, size);
sprint(tree_size);
// 구간 합 구하기 (배열의 l~r 구간에 대한 합을 세그먼트 트리로 구하기)
printf("[2,4]의 합:%d\n\n", sum(1, 0, size - 1, 2, 4)); // 특정 구간
/* ------------------------------------------------------------------ */
/* ------------------------------------------------------------------ */
// 업데이트 (배열의 idx번째 원소를 val로 바꿀 때 세그먼트 트리 업데이트)
int idx = 4;
int val = 5;
printf("업데이트: arr[%d]=%d -> %d\n", idx, arr[idx], val);
update(1, 0, size - 1, arr, idx, val); // arr[4]=4가 5가 되었을 때 세그먼트 트리 업데이트
// 배열 및 세그먼트 트리 출력
aprint(arr, size);
sprint(tree_size);
// 구간 합 구하기
printf("[2,4]의 합:%d\n", sum(1, 0, size - 1, 2, 4)); // 특정 구간
return 0;
}
세그먼트 트리 (구간 최댓값 구하기: Range Max Query)
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MAX(a,b) (((a) >= (b)) ? (a):(b))
int size;
int* s_tree;
int init(int* arr, int node, int s, int e) {
if (s == e)
return s_tree[node] = arr[s];
int m = (s + e) / 2;
return s_tree[node] = MAX(init(arr, node * 2, s, m), init(arr, node * 2 + 1, m + 1, e));
}
// s,e: 배열의 시작,끝 인덱스 (탐색하는 구간)
// l,r: 부분 배열의 시작,끝 인덱스 (MAX을 구하려는 구간)
int ret(int node, int s, int e, int l, int r) {
if (l > e || r < s)
return 0;
if (l <= s && e <= r)
return s_tree[node];
int m = (s + e) / 2;
return MAX(ret(node * 2, s, m, l, r), ret(node * 2 + 1, m + 1, e, l, r));
}
// s,e: 배열의 시작,끝 인덱스 (탐색하는 구간)
// idx: 배열의 특정 인덱스 (바꾸려는 원소)
// val: 바꿀 숫자
int _update(int node, int s, int e, int idx, int val) {
if (s <= idx && idx <= e) {
if (s == e) {
s_tree[node] = val;
}
else {
int m = (s + e) / 2;
s_tree[node] = MAX(_update(node * 2, s, m, idx, val), _update(node * 2 + 1, m + 1, e, idx, val));
}
}
return s_tree[node];
}
void update(int node, int s, int e, int* arr, int idx, int val) {
arr[idx] = val;
_update(node, s, e, idx, val);
}
// 배열 출력
void aprint(int* arr, int size) {
printf("배열: ");
for (int i = 0; i < size; i++) {
printf("[%d] %d ", i, arr[i]);
}
printf("\n");
}
// 세그먼트 트리 출력
void sprint(int size) {
printf("세그먼트 트리: ");
for (int i = 1; i < size; i++) {
printf("[%d] %d ", i, s_tree[i]);
}
printf("\n");
}
int main(void)
{
// 배열 선언 및 배열 크기(size) 초기화
int arr[] = { 0,1,2,3,4,5 };
size = 6;
// 세그먼트 트리 선언
int h = (int)ceil(log2(size));
int tree_size = (int)pow(2, h + 1);
s_tree = (int*)calloc(tree_size, sizeof(int));
// 세그먼트 트리 초기화 (arr 배열 이용)
init(arr, 1, 0, size - 1);
// 배열 및 세그먼트 트리 출력
aprint(arr, size);
sprint(tree_size);
// 구간 최댓값 구하기 (배열의 l~r 구간에 대한 최댓값을 세그먼트 트리로 구하기)
printf("[2,4]의 최댓값:%d\n\n", ret(1, 0, size - 1, 2, 4)); // 특정 구간
/* ------------------------------------------------------------------ */
/* ------------------------------------------------------------------ */
// 업데이트 (배열의 idx번째 원소를 val로 바꿀 때 세그먼트 트리 업데이트)
int idx = 4;
int val = 5;
printf("업데이트: arr[%d]=%d -> %d\n", idx, arr[idx], val);
update(1, 0, size - 1, arr, idx, val); // arr[4]=4가 5가 되었을 때 세그먼트 트리 업데이트
// 배열 및 세그먼트 트리 출력
aprint(arr, size);
sprint(tree_size);
// 구간 최댓값 구하기 (배열의 l~r 구간에 대한 최댓값을 세그먼트 트리로 구하기)
printf("[2,4]의 최댓값:%d\n\n", ret(1, 0, size - 1, 2, 4)); // 특정 구간
return 0;
}

