회귀 분석을 예시로 설명하면서 정규화와 표준화의 필요성을 알아 보겠습니다!

회귀 분석이란 ‘변수와 변수 사이의 관계를 알아보기 위한 통계적 분석 방법’ 입니다.

‘종속 변수와 독립 변수 사이의 관계를 알아보기 위한 분석‘ 이라고도 말합니다.

먼저 종속 변수와 독립 변수에 대해 알아 봅시다.

종속 변수는 분석의 대상이 되는 변수입니다.
독립 변수는 종속 변수에 영향을 미치는 변수입니다.

예시를 들어 보겠습니다.

‘월별 소득이 자녀의 수에 미치는 영향‘을 분석한다고 해봅시다!

이 때 분석할 변수는 자녀의 수입니다. (종속 변수)
자녀의 수에 영향을 미치는 변수는 월별 소득입니다. (독립 변수)

회귀 분석에 대한 간략한 소개는 여기까지 하고 아래의 그래프를 보겠습니다.

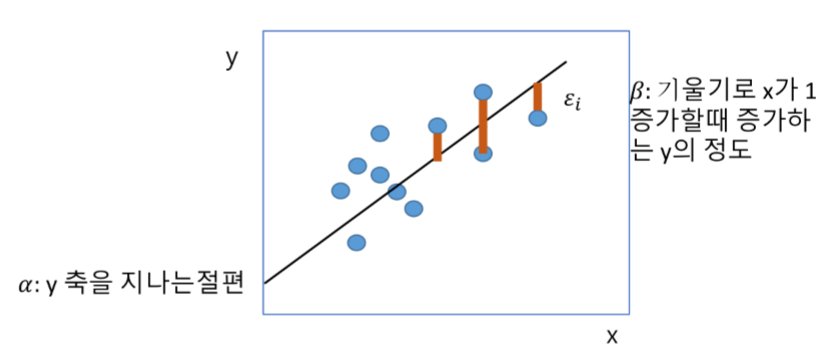
선형 방정식 y = a + bx의 그래프입니다.

위를 단순 선형 회귀 모델이라고 부릅니다.
하나의 종속 변수와 하나의 독립 변수 사이의 관계를 선형 방정식으로 나타낸 것입니다!
(x: 월별 소득, y: 자녀의 수)

그런데 과연 월별 소득(x)만이 자녀의 수(y)에 영향을 줄까요?
다시 말해, 독립 변수 하나(월별 소득)만으로 종속 변수(자녀의 수)를 구한다면 그것은 정확할까요?

물론 아닐 것입니다!
여러 독립 변수들이 사용돼야 더 의미있는 관계(회귀 모델)를 찾을 수 있을 것이고
그 관계(회귀 모델)를 이용해야 더 올바른 종속 변수(자녀의 수)의 값을 얻을 수 있을 것입니다!

그래서 이번에는 ‘나이’라는 독립 변수를 추가해보겠습니다!
즉 (나이, 월별 소득)과 자녀의 수와의 관계를 알아 보겠습니다.

관계(회귀 모델)를 시각화하면 아래와 같습니다!

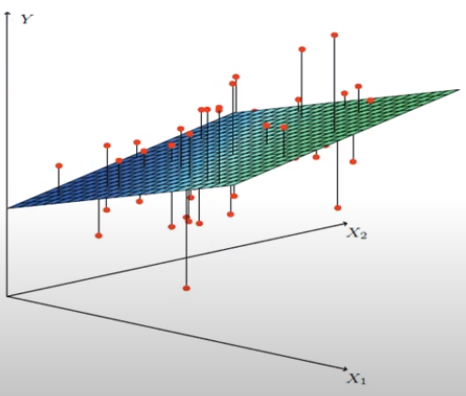
위를 다중 선형 회귀 모델이라고 부릅니다.
두 개 이상의 독립 변수와 하나의 종속 변수 사이의 관계를 나타낸 모델입니다!

두 개의 독립 변수를 사용할 때 모델의 식은
y = a + b1x1+ b2x2가 됩니다.
(y= b0 + b1x1 + b2x2라고도 부름)

이 모델을 이용하면
나이(x1)와 월별 소득(x2)이 입력으로 들어 갔을 때 자녀의 수(y)를 추론할 수 있습니다!

그런데 여기서 반드시 고려해야 될 점이 있습니다

두 독립 변수의 범위를 비슷하게 만들어야 된다는 점입니다!

사실 나이와 월별 소득의 범위는 차이가 큽니다!

우리는 나이의 범위가 [0~100]이고 월별 소득은 [0~10,000,000] 혹은 그 이상으로 예상해볼 수 있습니다!

그런데 이 데이터를 그대로 이용하면 소득이 더 크기 때문에 결과에 더 큰 영향을 미칠 수 밖에 없습니다!

y = a + b1x1+ b2x2라는 관계식에서
x1보다 x2가 훨씬 크므로 y값의 결정은 x2가 하는 것이나 다름이 없겠죠!

y(자녀의 수)를 더 정확하게 알기 위해 x1(나이)을 추가했는데..
x2(월별 소득)보다 값이 작다는 이유로 의미가 없어지게 된 것입니다!

그럼 정말로 x1(나이)은 의미가 없느냐?
당연히 그렇지 않습니다!
의미가 없으면 독립 변수를 추가할 이유가 없지요!

또한 값의 차이가 위처럼 엄청나게 크지는 않더라도
한 쪽이 더 의미있는 역할을 하면 우리의 의도와는 다른 관계(모델)가 형성됩니다.
위처럼 [ (x1,x2)-y의 관계]가 아니라 [x2-y의 관계]가 형성될 수 있다는 의미입니다!

이것을 편향된 모델(특정 데이터에 영향을 많이 받는 모델)이라고 합니다!

따라서 두 독립 변수가 모두 의미있게 사용되려면 범위를 비슷하게 만들어야 됩니다!

그 방법이 바로 정규화 혹은 표준화입니다!

정규화 (Normalization)

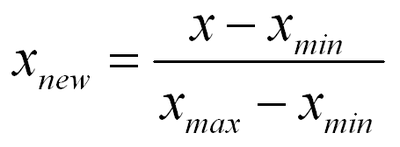
최소-최대 정규화는 데이터를 정규화하는 가장 일반적인 방법입니다!
데이터를 0과 1 사이의 값 [0,1]으로 변환하는 것입니다!

표준화 (standardization)

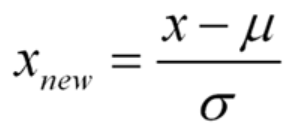
표준화는 평균을 빼고 표준편차로 나누는 작업입니다!
이렇게 되면 X는 평균이 0, 표준편차가 1인 정규분포를 따르게 됩니다!

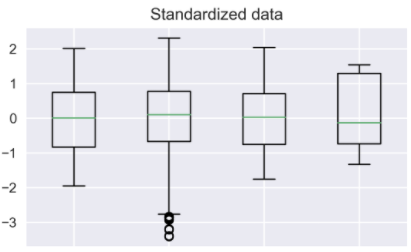
표준화를 할 때는 데이터의 min,max가 정해져 있지 않아 outlier를 확인할 수 있는데
이렇게 특정 범위를 벗어난 데이터는 제거하고 이용할 수도 있습니다!

머신러닝에서 정규화의 효과

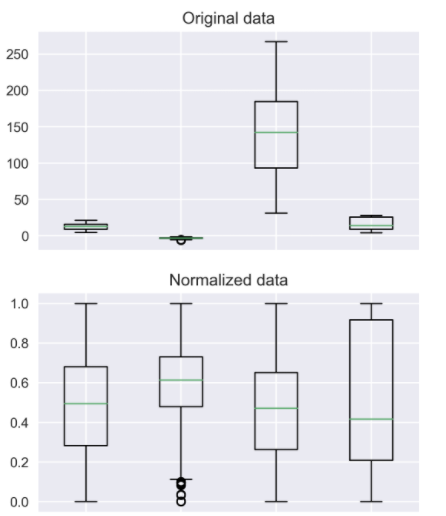
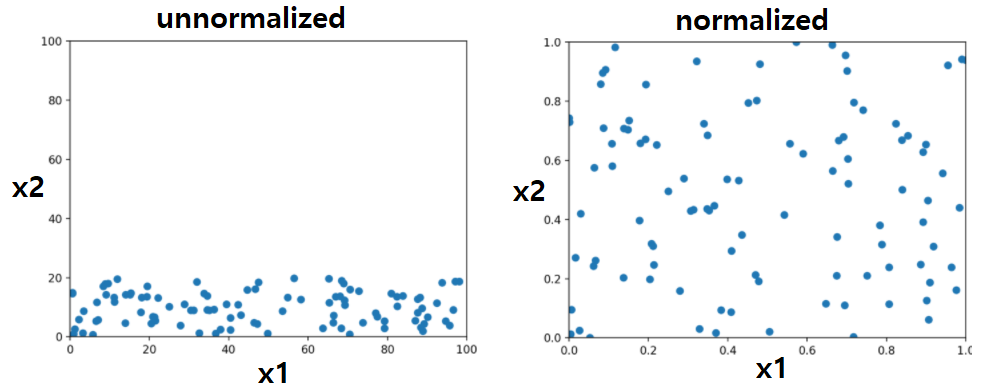
정규화 혹은 표준화를 이용하면 데이터의 형태가 변하게 됩니다!
아래는 x1 feature, x2 feature 각각에 대해 MIN-MAX 정규화를 한 형태입니다.

머신러닝에서 중요한 Loss Function – J함수도 입력(x)을 정규화함에 따라 형태가 변하게 됩니다!

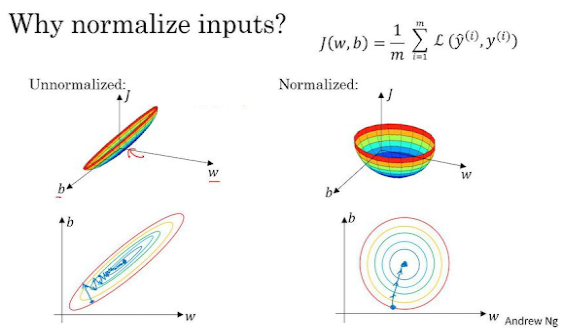
원래는 Elongated(가늘고 길죽한)되어 있지만 정규화 후에는 Spherical(구 모양)이 되는 것이죠!

이렇게 정규화를 했을 때 Optimal Solution을 더 빠르게 찾아간다는 효과가 있다고 합니다!

참고로 딥러닝은 입력층의 결과가 다시 은닉층의 입력으로 들어오는 구조입니다.
은닉층의 입력에는 Weighted sum과 activation function을 거친 결과가 들어 오는데
이것 때문에 입력층의 입력이 정규화됐다고 하더라도 다음 층의 입력은 다시 비정규화된 형태로 변하게 됩니다.
따라서 딥러닝 네트워크 사이에 BN(Batch Normalization)층을 많이 추가하면서 강제적으로 정규 분포를 만든다고 합니다.

마무리

사실 정규화와 표준화를 좀 더 쉽게 설명한 포스팅도 많습니다!

예를 들어 bskyvision님의 포스팅을 참고하면

Q. 수학 시험과 영어 시험을 봤는데 수학 점수는 평균이 80점이고 표준편차가 20이었고, 영어 점수는 평균이 60이고 표준편차가 10였다. 이런 상황에서 자녀가 수학을 90점 맞았고, 영어를 80점 맞았다면 어떤 것을 더 칭찬해줘야 할까?

라는 문제가 주어질 때,
“공정한 상대 평가를 위해 두 분포를 동일하게 만들 필요가 있고 그 과정(분포를 동일하게 만드는 과정)이 표준화야” 라고 간단하게 설명할 수도 있습니다!

그리고 정규 분포와 식으로 설명을 뒷받침하면 됩니다!

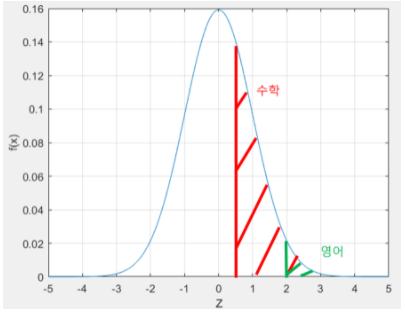
P(X>=90) = P(Z>=(90-80)/20) = P(Z>=0.5) = 0.3085 <수학(X)은 상위 30% 성적>
P(Y>=80) = P(Z>=(80-60)/10) = P(Z>=2) = 0.0228 <영어(Y)는 상위 2% 성적>
-> 영어 점수를 더 칭찬해줘야 함!!

따라서 제가 쓴 글을 난해하다고 평가할 수도 있습니다!
그러나 머신러닝의 회귀 문제와 overlap한다면 머신러닝 관점에서도 정규화의 필요성을 파악할 수 있지 않을까?
라고 생각하였습니다.

모든 독립 변수들이 의미있게 사용되기 위해 범위를 비슷하게 만들어야 된다는 말은
머신러닝 관점에서 모든 입력 Feature들이 의미있게 사용되기 위해 범위를 비슷하게 만들어야 된다는 말과 같습니다! 이렇게 해야 학습 성능도 더 증진될 것입니다!

bskyvision님의 글이나 저의 글이나 정규화의 핵심은
모든 데이터를 동일 선상에서 같은 의미로 바라 봐야지 의미있는 정보를 획득할 수 있다는 것입니다!
[시험 점수 예시: 서로 다른 시험 점수(수학, 영어)들을 동일 선상으로 봐야 한다]
[회귀 분석 예시: 서로 다른 feature(나이, 소득)들을 동일 선상으로 봐야 한다]

이 핵심만 파악하신다면 앞으로 어떠한 문제를 풀더라도 정규화를 잊지 않을 것이라 단언합니다.

지금까지 긴 글을 읽어 주셔서 감사합니다.
또한 정규화에 대해 많은 정보를 제공해주신 블로거 분들에게도 감사합니다.

참고 자료

1.  정규 분포와 정규 분포의 표준화의 의미
https://bskyvision.com/48

2. [통계] 정규화(Normalization) vs 표준화(Standardization)
https://heeya-stupidbutstudying.tistory.com/32

3. 정규화(Normalization) 쉽게 이해하기
https://hleecaster.com/ml-normalization-concept/

4. [머신러닝/딥러닝] 8. Normalization
https://sonsnotation.blogspot.com/2020/11/8-normalization.html

5. Mining – 회귀 분석
https://shacoding.com/2019/12/08/mining-%ed%9a%8c%ea%b7%80-%eb%b6%84%ec%84%9d/