Gradient Vanishing
DNN은 히든 레이어가 2개 이상인 신경망입니다.
일반적으로 딥러닝은 층을 깊게 할수록 좋습니다.
1. 중간에 Activation Function이 추가돼서 비선형성을 늘립니다.
2. 층이 깊어져서 모델 복잡도가 증가되면 정확도가 높아지는 경향이 있습니다.
3. 층을 깊게 하면 신경망의 매개변수(w)가 줄어들게 됩니다. (일부 모델 한정)
하지만 층을 깊게 하면 치명적인 문제가 발생합니다.
바로 ‘Gradient Vanishing’이라는 문제입니다.

역전파가 Input Layer 방향으로 진행될수록 Gradient 값이 미약해진다는 의미입니다.
이 문제는 1986~2006년에 밝혀졌는데,
이것 때문에 딥러닝이 불가능해지고 SVM 같은 다른 모델이 만들어지게 됩니다.
그리고 추후 Vanishing을 어느 정도 해결해주는 여러 방법이 나오게 되었습니다.
일단 Activation Function을 sigmoid로 한 것이 문제라는 의견이 나와서
relu로 변경하자 어느 정도 해결되는 모습을 보였습니다.
두 번째는 Batch Normalization을 추가하는 것입니다.
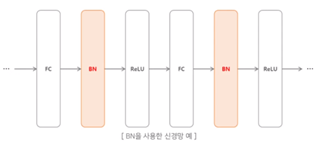
말 그대로 batch사이즈만큼 normalization을 한다는 의미입니다.
Gradient가 Vanishing하는 이유는 레이어를 거치면서 분포(output으로 나온 값의 분포)가 일정하지 않기 때문이라는 의견이 나왔습니다. (internal covariate shift)
그래서 이 분포를 고르게 하기 위해서 정규화를 하는 것입니다.

위에 보이는 식들을 이용해서 분포를 강제적으로 정규 분포에 맞게 만듭니다.
또한 이 방법을 사용하면 딥러닝을 하는데 다른 이점도 준다고 합니다.
Batch Normalization의 특징은 아래와 같습니다.
1. Gradient Vanishing 감소 (Exploding도 감소)
2. 가중치 초기화에 덜 민감
3. 학습률을 크게 잡아도 gradient descent 잘 수렴
4. 일반화(regularization) 효과 -> 오버피팅이 잘 안 일어남
model.fit 함수 parameter 소개
아래는 fit함수의 parameter에 대한 소개입니다. (이전 설명 보완)
history=model.fit(X,y,
batch_size=20,
epochs=20,
steps_per_epoch=len(x_train)//batch_size,
validation_steps=len(x_val)//batch_size,
verbose=0)
X: feature vector[입력]
y: target vector[정답]
batch_size: 학습을 할 때 얼마나 많은 데이터를 이용할 것인가 (기본 값:32)
epochs: 전체 데이터를 이용해서 얼마나 학습할 것인가
steps_per_epoch: 한 에포크 당 스텝 수(weight, bias 업데이트 수)
validation_steps: (사용자 지정)스텝 수마다 검증을 한 번 하겠다. (원래 1epoch당 1번 검증)
[ step: batch_size 기준 학습 수 (batch_size만큼 처리한 다음 weight, bias 업데이트 한 것을 1번으로 취급)
epoch: 전체 데이터 기준 학습 수 (전체 데이터를 처리한 다음 weight, bias업데이트 한 것을 1번으로 취급) ]
(예시)
len(x_train)=120, len(x_val) = 40
steps_per_epoch = len(x_train) // batch_size = 120 // 20 = 6
-> 한 에포크 당 스텝을 6번하는데 20개 데이터(batch_size)를 처리할 때마다 하겠다.
-> 1 epoch: 20 (step) 20 (step) 20 (step) 20 (step) 20 (step) 20 (step)
validation_steps = len(x_val) // batch_size = 40 // 20 = 2
-> 스텝 2번마다 검증을 한 번 하겠다.
-> 1 epoch: 20 (step) 20 (step) (val) / 20 (step) 20 (step) (val) / 20 (step) 20 (step) (val)
감사합니다.
