조합

서로 다른 n개의 원소로 중복 없이 r개를 선택하는 방법

(동치 문제) 서로 다른 n개의 카드 중 r개를 중복 없이 뽑는 방법

ex) 3C2 -> 12, 13, 23
ex) 4C3 -> 123, 124, 134, 234

경우의 수 공식: n! / (n-r)!r! = n(n-1)(n-2)….(n-r+1) / r!
ex) 3C2 -> 3*2 / 2*1 = 3
ex) 4C3 -> 4*3*2 / 3*2*1 = 4

조합 나열 코드: (링크)

중복조합

서로 다른 n개의 원소로 중복을 허용해서 r개를 선택하는 방법

(동치 문제) 서로 다른 n개의 카드 중 r개를 뽑는 방법 (중복  허용)

ex) 3H2 -> 11, 12, 13, 22, 23, 33
ex) 4H3 -> 111, 112, 113, 114, 122, 123, 124, 133, 134, 144, 222, 223, 224, 233, 234, 244, 333, 334, 344, 444

경우의 수 공식: n+r-1Cr
ex) 3H2 -> 4C2 = 4*3 / 2*1 = 6
ex) 4H3 -> 6C3 = 6*5*4 / 3*2*1 = 20

중복조합 나열 코드: (링크)

순열

서로 다른 n개의 원소로 중복 없이 r개를 선택하고 나열하는 방법

(동치 문제) 서로 다른 n개의 카드 중 r개를 중복 없이 뽑고 r자릿수를 만드는 방법

ex) 3P2 -> 12, 13, 21, 23, 31, 32
ex) 4P3 -> 123, 124, 132, 134, 142, 143, 213, 214, 231, 234, 241, 243, 312, 314, 321, 324, 341, 342, 412, 413, 421, 423, 431, 432

경우의 수 공식: n! / (n-r)! = n(n-1)(n-2)….(n-r+1)
ex) 3P2 -> 3*2 = 6
ex) 4P3 -> 4*3*2 = 24

순열 나열 코드: (링크)

중복순열

서로 다른 n개의 원소로 중복을 허용하여 r개를 선택하고 나열하는 방법

(동치 문제) 서로 다른 n개의 카드 중 r개를 뽑고 r자릿수를 만드는 방법 (중복 허용)

ex) 3𝝿2 -> 11, 12, 13, 21, 22, 23, 31, 32, 33
ex) 4𝝿3 -> 111, 112, 113, 114, 121, 122, 123, 124, 131, 132, 133, 134, 141, 142, 143, 144, 211, 212, 213, 214, 221, 222, 223, 224, 231, 232, 233, 234, 241, 242, 243, 244, 311, 312, 313, 314, 321, 322, 323, 324, 331, 332, 333, 334, 341, 342, 343, 344, 411, 412, 413, 414, 421, 422, 423, 424, 431, 432, 433, 434, 441, 442, 443, 444

경우의 수 공식: n^r
ex) 3𝝿2 -> 3^2 = 9
ex) 4𝝿3 -> 4^3 = 64

중복순열 나열 코드: (링크)

자연수의 분할

어떤 자연수 n을 k개의 합으로 나타내는 방법

(동치 문제) 똑같이 생긴 n개의 공을 k개의 같은 상자에 빈 상자없이 나누는 방법

ex) P(4,2) -> 3+1, 2+2
ex) P(5,3) -> 3+2+1, 2+2+1

경우의 수 공식: [사진 참고]

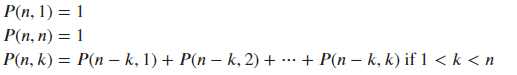
자연수의 분할 나열 코드: (링크)

집합의 분할

서로 다른 n개의 원소를 지닌 집합을 겹치지 않도록 k개의 부분집합으로 나누는 방법

(동치 문제) 서로 다른 n개의 공을 k개의 같은 상자에 빈 상자없이 나누는 방법

ex) S(4,2) -> 3+1 [4C3 x 1C1], 2+2 [4C2 x 2C2 x 1/2!]
ex) S(5,3) -> 3+2+1 [5C3 x 2C1 x 1C1 x 1/2!], 2+2+1 [5C2 x 3C2 x 1C1 x 1/2!]

– n을 k개로 분할하는 경우를 찾고 조합을 이용하여 방법의 수를 찾음
– 팩토리얼로 나누는 이유는 중복을 제거하기 위함 ex) 12/34와 34/12는 같음

경우의 수 공식: [사진 참고]

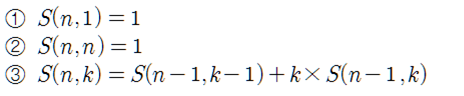
집합의 분할 나열 코드: (링크)