딥러닝과 학습
딥러닝은 여러 방법으로 정의할 수 있습니다.
필자는 ‘머신러닝의 학습 전략 중 ANN을 발전시킨 학문’이라고 생각합니다.
실제로 MLP의 히든 레이어가 2개 이상인 것부터 DNN이라고 합니다.
DNN은 Deep Neural Network, 즉 딥러닝입니다.

처음 소개하는 딥러닝 모델은 [ ANN 이론 ]에서 소개한 것과 비슷합니다.
히든 레이어가 더 많아져서 복잡해졌을 뿐입니다.
똑같이 출력층에서 나온 값으로 예측을 하고, Activation Function을 이용한다면 분류 문제를 풀 수 있습니다.
그리고 딥러닝도 마찬가지로 학습을 합니다.
일단 머신러닝으로 돌아가보겠습니다.
머신러닝은 ‘컴퓨터가 학습을 하는 방법에 대해 다루는 학문’이며,
학습은 ‘데이터의 패턴을 파악하는 과정’입니다.
즉 어떠한 과정, 방법, 알고리즘 따위를 겪으면 데이터의 패턴이라는 결과가 나온다는 것이죠.
예를 들어,
클러스터링은 센터를 계속 업데이트하는 학습(과정)으로 데이터가 어떻게 그룹핑되는지 확인할 수 있습니다.
의사 결정 나무는 엔트로피가 적은 방향으로 구간을 나누는 학습(과정)으로 데이터가 어떻게 분류되는지 확인할 수 있습니다.
선형 회귀는 Gradient Descent를 이용한 Loss를 줄이는 학습(과정)으로 데이터 계형을 나타내는 회귀 곡선을 그릴 수 있습니다.
ANN은 선형 모델에 활성화 함수를 추가하고 Loss를 줄이는 학습(과정)을 해서 데이터를 분류시키는 결정 경계(Decision Boundary)를 그릴 수 있습니다.
딥러닝의 학습은 ANN과 비슷합니다.
1. w를 임의로 정하고 Loss(J(W)) 값을 구합니다.
2. Loss값을 작게 하기 위해 Gradient를 이용해서 w를 업데이트합니다. (w<- w – (learning rate) * dJ(W)/dw)
3. Loss가 최소가 되는 w를 찾을 때까지 (2)를 반복합니다.

즉 딥러닝에서 말하는 학습이란 ‘Loss(손실 함수)를 최소로 만드는 가중치를 찾는 작업’입니다.
이 학습 결과로 결정 경계를 얻으면 새로운 데이터를 분류할 수 있고 (classification)
activation function을 제외해서 회귀 곡선만 얻는다면 입력치에 대한 실수 값을 예측할 수 있습니다. (regression)
앞으로 이러한 딥러닝에 대해 체계적으로 알아 보겠습니다.
Forward Propagation (순방향 패스, 순전파)
입력 신호가 입력층과 은닉층을 통하여 출력층으로 전파되는 과정입니다.
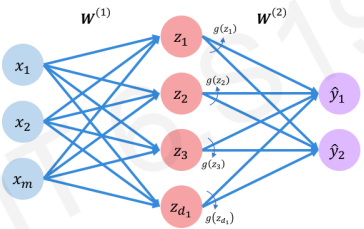
전파를 할 때는 [ 활성화 함수에 (입력 신호와 가중치를 곱한 값들의 합)을 넣고 반환된 값 ]을 전파합니다.
아래 그림으로 따지면 g(x1w2+x2w2+xmwm)을 다음 노드에 전파하는 것입니다.
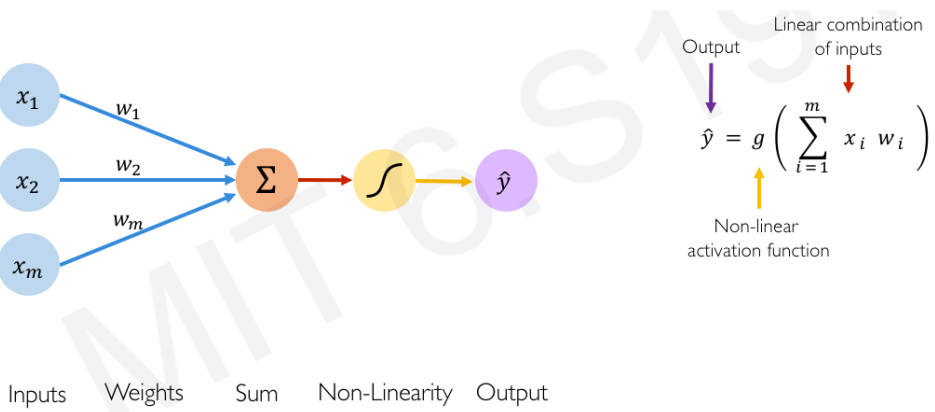
출력층에서 나온 값이 실수이면, 실수를 예측하였으니 회귀 문제를 푼 것이고
출력층에서 활성화 함수를 거쳐서 값이 나왔으면 레이블을 예측하였으니 분류 문제를 푼 것입니다.
Backward Propagation (역방향 패스, 역전파)
출력층에서부터 오차를 역으로 전파하는 과정입니다.
이 과정에 의해 모든 위치에서의 dJ(W)/dw를 구할 수 있고, dJ(W)/dw로 w를 업데이트할 수 있습니다.

(1) 출력층 전에 위치한 가중치 구하기 (w2로 부름)
w2를 구하려면 ‘출력층 노드의 오차 : dJ(W) / dy^’가 필요합니다.
[ dJ(W) / dy^ ]가 존재하면 체인룰(연쇄법칙)에 의해 [ dJ(W)/dw2 ]를 구할 수 있습니다.
[ dJ(W)/dw2 ] 를 구했으면 w2를 구할 수 있습니다. (w2<- w2 – (learning rate) * dJ(W)/dw2)
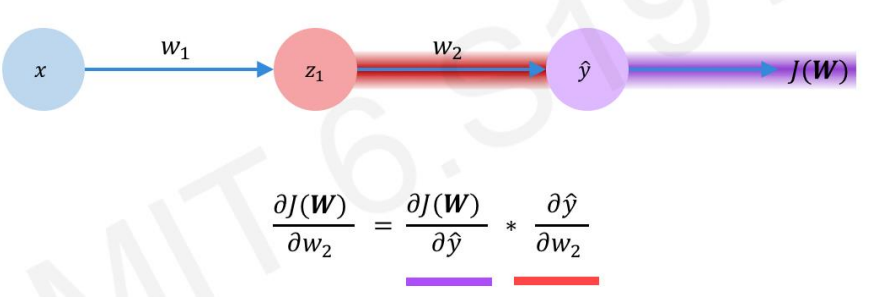
(2) 은닉층 전에 위치한 가중치 구하기 (w1으로 부름)
w1을 구하려면 ‘다음 은닉층 노드의 오차 : dJ(W) / dz1’가 필요합니다.
[ dJ(W) / dz1 ]이 존재하면 체인룰(연쇄법칙)에 의해 [ dJ(W)/dw1 ]을 구할 수 있습니다.
[ dJ(W)/dw1 ] 를 구했으면 w1을 구할 수 있습니다. (w1<- w1 – (learning rate) * dJ(W)/dw1)
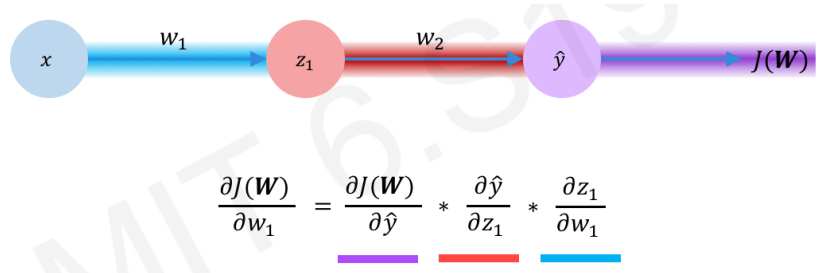
그런데 위 식을 자세히 보면 [ dJ(W) / dz1 ] 을 구하기 위해 [ dJ(W) / dy^ ] 를 이용합니다.
즉 현재 w의 그래디언트를 구하려면 다음 레이어들의 오차가 필요합니다.
따라서 출력층에서부터 오차를 역전파하는 것입니다.
TMI) (dJ(W) / dy^, dJ(W) / dz1, ..) 와 같은 미분 식을 전개하였을 때 (out-target*k) 따위의 식이 나오는데, 이는 오차에 어떤 값을 곱한 형태이기 때문에 그냥 ‘오차’라고 부른다고 생각합니다.
딥러닝 모델 제작
이제 Tensorflow 코드로 딥러닝 모델을 제작해보겠습니다.
Tensorflow에 대한 설명은 (링크)를 참고해주세요!!
model=tf.keras.Sequential([
tf.keras.layers.Dense(units=4,activation='sigmoid',input_shape=(3,)),
tf.keras.layers.Dense(units=2,activation='sigmoid')
])
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.3),loss='mse')
model.summary()
위는Sequential API를 이용해서 딥러닝 모델을 만드는 방법입니다.
tensorflow.keras의 Dense객체는 층(layer)이라고 생각하면 됩니다.
파라미터에 (레이어의 노드 수, activation function, 이전 레이어의 노드 수[생략 가능])을 넣어서 층을 생성합니다.
은닉층의 노드 수는 자유롭게 설정해도 괜찮습니다.
Regression 문제를 풀 경우에는 출력층에 activation function을 넣지 않습니다.
위 코드에 의하면 (입력층 (노드:3) – 은닉층 (노드:4) – 출력층 (노드:2))인 모델이 만들어집니다.
각 노드에서 활성화 함수는 sigmoid가 적용됐습니다.

model.compile함수는 만든 모델에 [optimizer, loss function]을 지정하는 것입니다.
optimizer를 지정할 때 learning rate도 지정할 수 있습니다.
optimizer는 최적화 방법입니다.

SGD(Stochastic Gradient Descent) 같은 경우, 일반 GD(Gradient Descent)보다 loss를 빨리 줄이지만 정확성은 떨어지는 최적화 방법입니다.
이러한 단점을 극복하기 위해서 Adam, Adadelta, RMSProp 등과 같은 여러 Optimizer가 나왔다고 생각하면 됩니다.
# 모델 훈련 model.fit(X,y,batch_size=1,epochs=1000,verbose=0) # 모델 테스트 print(model.predict(X))
이번에는 본격적으로 모델을 훈련해보겠습니다.
모델 훈련에 필요한 fit 함수의 파라미터에는 (feature vector[입력], target vector[정답], 배치 사이즈, 에포크)가 들어 갑니다. verbose같은 경우 0을 주면 학습 진행 상황을 안 보이게 합니다.
배치 사이즈(batch_size)는 학습을 할 때 얼마나 많은 데이터를 이용할 것인가에 대해 정하는 것입니다.
배치 사이즈를 정하지 않으면 32개의 데이터를 이용해서 학습하게 됩니다.
즉 입력층에 32개의 데이터를 주고 Backpropagation을 하고 가중치(w)를 업데이트합니다.
배치 사이즈가 1이면 한 개의 데이터를 이용해서 학습하게 됩니다.
즉 입력층에 데이터 한 개를 주고 Backpropagation을 하고 가중치(w)를 업데이트합니다.
에포크(epochs)는 전체 데이터를 이용해서 얼마나 학습할지에 대해 정하는 것입니다.
예시를 들어 보겠습니다.
전체 데이터가 4개일 때 (batch_size=1, epochs=20)이라면 몇 번이나 학습할까요??
전체 데이터 기준으로는 20번 학습합니다.
하지만 (1개 데이터 기준으로 4번 학습)할 때, 전체 데이터 기준으로 한 번 학습하게 됩니다.
따라서 iteration 기준으로는 80(4×20)번 학습하는 것입니다.
모델 훈련까지 완료됐으면 model.predict를 통해 x에 대한 예측치를 구할 수 있습니다.
모델 제작에 대한 설명은 여기까지입니다.
보다 나은 이해를 위해 AND 분류에 대한 파이썬 코드를 제공하겠습니다.
# Sequential API로 and 분류 모델 만들기
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# 입력 값과 타깃 값 (데이터 4개)
x=np.array([[1,1],[1,0],[0,1],[0,0]])
y=np.array([[1],[0],[0],[0]])
# 모델 생성
model=tf.keras.Sequential([
tf.keras.layers.Dense(units=2,activation='sigmoid',input_shape=(2,)),
tf.keras.layers.Dense(units=1,activation='sigmoid')
])
# 모델 컴파일
model.compile(optimizer=tf.keras.optimizers.SGD(lr=0.3),loss='mse')
# 모델에 대한 정보 출력
model.summary()
# 모델 훈련 (훈련 정보 history에 저장)
history=model.fit(x,y,epochs=1000)
# 모델을 이용해서 x예측 -> 4개의 정답 나옴
output=model.predict(x)
print(output)
# loss 줄어드는 것을 그래프로 확인
plt.plot(history.history['loss'])

위 모델로 800번 이상 학습할 때 loss값은 0.04보다 작은 것을 확인할 수 있습니다.
이 그래프를 보면 굳이 1000번이나 학습할 필요가 없다는 것을 알 수 있습니다.
이런 경우 epoch를 줄이는 것이 공간과 시간 면에서 효율적입니다.
반대로 loss값이 잘 줄어들지 않으면 epoch를 늘리거나 모델을 수정하는 방식으로 해결하면 됩니다.
그런데 만약 그래프가 아래와 같은 형태면 어떻게 해결해야 될까요?
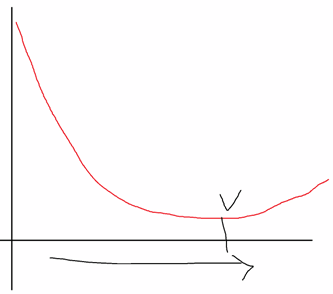
그냥 Loss가 가장 낮을 때 학습을 중단하면 되지 않을까요?
이런 경우 earlyStopping이라는 기술을 도입합니다.
쉽게 말해 loss function 값들을 함수로 그렸을 때 계형이 다시 올라가기 전까지만 확인하는 방법입니다.
아래는 earlyStopping를 이용하는 fitting 코드입니다.

earlyStopping 기술은 아래와 같이 오버피팅이 일어났을 때도 사용할 수 있습니다.
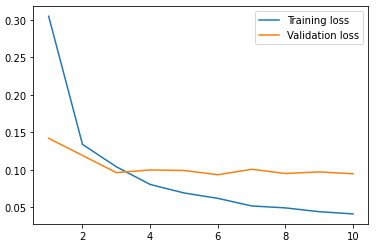
훈련 데이터의 손실값은 계속 줄어드는데, 검증 데이터의 손실값이 오히려 증가한다는 것은 오버피팅의 증거가 됩니다.
사실 이러한 오버피팅이 일어났을 때는 여러 가지 대처법이 있습니다. 간단히 정리하면 아래와 같습니다.
- 조기 종료: 검증 손실이 증가하면 훈련을 조기에 종료한다.
- 가중치 규제 방법: 가중치의 절대값을 제한한다. (ex) L2 Norm)
- 데이터 증강 방법: 데이터를 많이 만든다.
(데이터가 적으면 해당 데이터의 특정 패턴이나 노이즈까지 쉽게 학습하므로 일반화의 오류가 생길 수 있음. 예를 들어 레코드 간의 거리가 모두 가까운 줄 알았더니 특정 집단에서만 일어나는 특징임, A라는 벡터가 노이즈가 아닌 줄 알고 학습에 반영했는데 전체적으로 봤을 때는 노이즈 벡터임 -> 검증이나 테스트 결과에 악영향을 줌 -> 데이터를 늘려서 해결함[translation, rotation, stretching, shearing 방법을 이용해서 데이터를 늘림]) - 드롭아웃 방법: 학습 과정에서 무작위로 뉴런의 부분집합을 제거한다.
(학습을 하다 보면 어떤 특정한 feature찾기에 몰릴 수 있음. 예를 들어 고양이 분류 학습에서 (털,꼬리,장난스런 이미지)라는 특징 찾기에 몰릴 수 있음. 즉 비중이 높은 노드(털에 대한 특징을 찾는 노드들, 꼬리에 대한 특징을 찾는 노드들 등)에만 집중해서 학습이 되는 경향이 있음[weight가 한 쪽으로 치우쳐 짐]. 이 결과 오버피팅이 발생하게 됨(학습 데이터의 털,꼬리가 강조된 이미지만 잘 분류되고 일반적인 이미지 분류 성능은 낮음). 따라서 무작위로 뉴런을 제거하면서 비중이 높은 노드 일부를 삭제하면 해결됨)
딥러닝 의의
지금까지 (딥러닝에 대한 소개, 순전파-역전파, 모델 제작)에 대해 알아 보았습니다.
그런데 딥러닝은 왜 사용하는 것일까요?
영상처리를 예시로 설명하겠습니다.
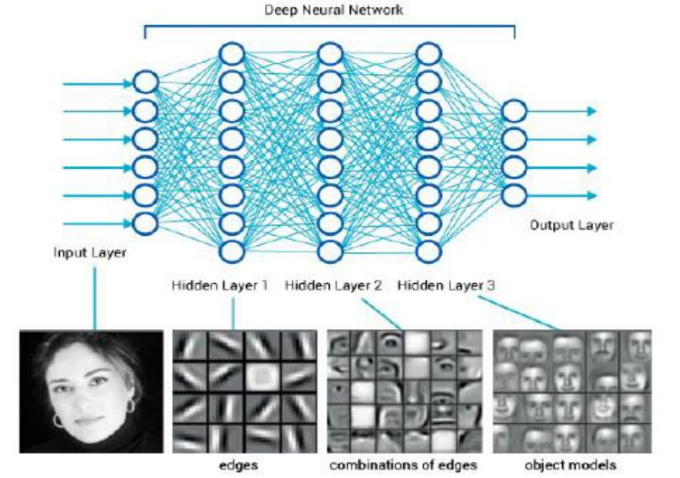
영상이 입력으로 들어갔을 때, 초반 레이어를 통과했을 때는 점,경계선을 추출할 수 있습니다.
중간 레이어를 통과했을 때는 영상의 영역(부분)에 대한 특징들을 추출할 수 있습니다.
후반 레이어를 통과했을 때는 영상의 큰 영역에 대한 특징들을 추출할 수 있습니다.
즉 레이어를 통과할 수록 높은 레벨의 특징을 추출할 수 있다는 것입니다.
이것을 이용해서 영상 분류와 같은 여러 가지 영상처리를 할 수 있습니다.
결국 딥러닝은 높은 레벨의 특징을 추출하기에 적합한 구조이므로
(영상 처리, 자연어 처리 등)에서 좋은 결과를 보입니다.
그러니 high level 특징을 요구하는 다양한 분야에서 딥러닝을 사용하는 것입니다.
감사합니다.
