선형 모델(Linear Model)을 파이썬으로 직접 구현해보겠습니다.
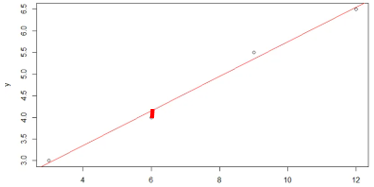
위는 간단한 단순 선형 모델입니다.
실제 데이터(o)들과 선형 모델이 예측한 값의 차이가 적도록 모델을 만들어야 됩니다!
차이(굵은 빨간 선)가 작을수록 실제 값과 잘 맞는다는 의미이고 새로운 데이터에 대해서도 예측을 잘할 가능성이 커집니다!
이 문제를 풀기 위한 기계학습 방법론 3단계를 소개합니다!
1단계) 모델 선택
-> 선형 회귀 모델(y=w0x+w1)로 학습시키겠다.
(=) 선형 회귀 모델을 생성하겠다.
2단계) 목적 함수(Loss function) 정의
-> 모델 품질을 체크 하기 위해 함수 ‘J(w)’를 정의하겠다.
(=) 품질이 좋은 모델을 생성하기 위해 함수 ‘J(w)’를 이용하겠다.
-> J(w)함수를 이용하면, 적절한 w0(기울기)와 w1(절편)을 찾을 수 있다.
[J(w)는 평균제곱오차함수가 됨, (y:예측 값-t:실제 값)들 여러 개를 합치고 평균 짓는 함수]
3단계) 최적화(Optimization)
-> 예측치와 실제 값의 오차가 가장 적게 되도록 J(w)를 최소화하고, 그때의 w0와 w1을 찾겠다.
(=) J(w)를 최소화하는 방법으로 품질이 좋은 모델을 찾겠다.

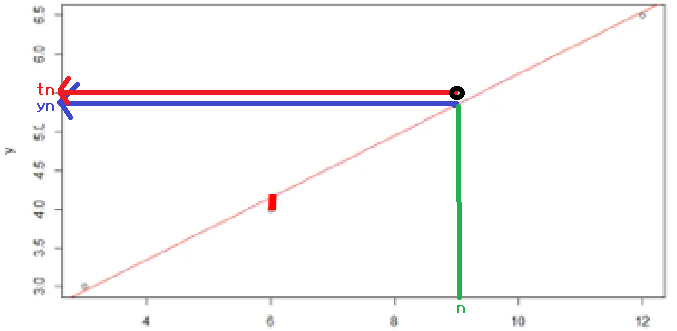
< Loss function : MSE >
(yn = 예측 값, tn = 실제 값)
(yn-tn)의 절댓값이 작아야 좋음!
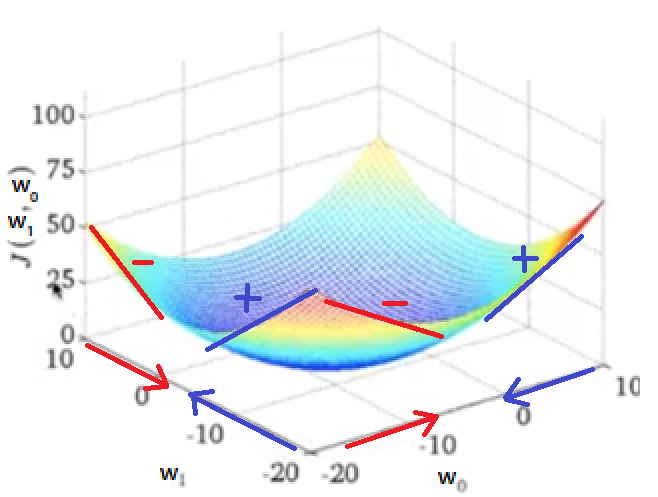
기울기(Gradient)를 이용한 최적화
J함수(Loss)는 평균 제곱 오차 함수로 다음과 같은 3차원 형태를 띕니다.
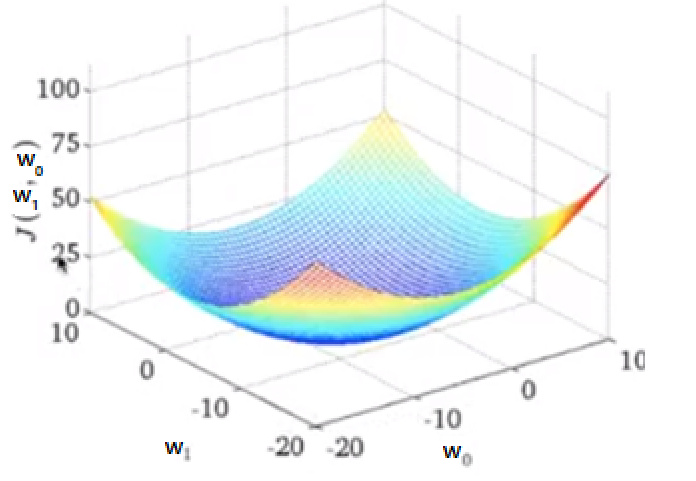
우리는 극값을 구하는 방식으로 최적화를 할 것입니다.
실제는 3차원 형태이지만 쉽게 생각하기 위해 2차 함수 계형처럼 생각합시다!
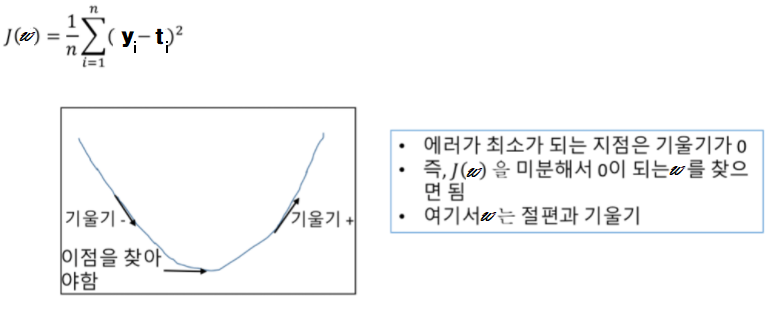
| (y-t) | 의 차이가 적을수록 좋은 모델이니까 J(w)를 최소화할 필요가 있고,
이는 J(w)가 극값일 때 성립합니다!
우리는 이 때 경사하강법(Gradient Descent)이라는 알고리즘을 사용합니다!
함수의 임의의 점을 Gradient(기울기)의 절댓값이 감소하는 방향(경사가 낮아지는 방향)으로 계속 변동해서 극값을 구하는 방식입니다.
그러나 완전한 극값을 구하기는 힘들 수 있으니까 기울기가 0이랑 가장 비슷한 값을 구하면 최적화가 완료됩니다.
그리고 최적화에 해당하는 w(w0, w1)를 구하면 최적의 모델을 구현할 수 있습니다!
파이썬을 이용한 구현
그럼 어떻게 해야 Gradient가 감소하는 방향으로 점을 변동할 수 있을까요?
지금부터 J함수의 입력에 해당하는 w에 대한 수식을 알아 보겠습니다.
해당 수식은 경사하강법을 내포하고 있습니다.
w(k+1)=w(k)-α∇J

w(k)는 J함수의 k번째 입력이고
w(k+1)은 업데이트된 w로써 J함수의 k+1번째 입력이 됩니다.
∇J = (D_w0, D_w1) <기울기 벡터>이고
여기서 D_w0는 J를 w0에 대해서 편미분한 값입니다.
(D_w1는 J를 w1에 대해서 편미분한 값)
α는 상수입니다. α가 클수록 기울기 변화를 심하게 합니다.
수식을 잘 보면,
기울기(∇J)가 +방향이면 w(k+1)은 w(k)보다 작게 업데이트됩니다. (w는 -방향으로 업데이트)
기울기(∇J)가 –방향이면 w(k+1)은 w(k)보다 크게 업데이트됩니다. (w는 +방향으로 업데이트)
즉 w는 기울기 방향과 반대로 업데이트되고,
업데이트된 w가 다시 J함수의 입력으로 들어갔을 때는 이전보다 작은 값을 반환합니다!
이러한 (업데이트-입력)를 반복하면 결국 극값과 가까운 결과를 반환하게 됩니다!!
w(w0, w1) 수식을 따로따로 생각하면 다음과 같습니다.
기울기 수식: w0(k+1) = w0(k) – α(D_w0)
절편 수식: w1(k+1) = w1(k) – α(D_w1)
그럼 이제 ∇J(D_w0, D_w1) 를 계산하는 함수를 알아 보겠습니다!
# return gradient of j
def grad_loss(x,t,w0,w1):
y=w0*x+w1
grad_w0=2*np.mean((y-t)*x)
grad_w1=2*np.mean(y-t)
return grad_w0, grad_w1
grad_w0는 gradient_w0이고 D_w0입니다.
J= 1/n * Σ {(y-t)^2}에서 중괄호 안쪽을 다르게 표현하면
(w0*x+w1-t)^2가 됩니다.
이것을 w0에 대해서 편미분하면 2(w0*x+w1-t)*x가 되는데, 이렇게 편미분한 값들을 평균지으면 grad_w0(D_w0)이 완성됩니다.
이를 코드로 작성하면 ‘grad_w0=2*np.mean((y-t)x)’가 됩니다!
grad_w1는 gradient_w1이고 D_w1입니다.
앞과 같은 방식으로 J를 w1에 대해서 편미분하면 2(w0*x+w1-t)가 되는데, 이렇게 편미분한 값들을 평균지으면 grad_w1(D_w1)이 완성됩니다.
이를 코드로 작성하면 ‘grad_w1=2*np.mean(y-t)’가 됩니다!
∇J를 구하는 함수를 만들었으니 이제 ‘경사하강법’을 이용해봅시다!
def grad_descent(x,t,w0,w1,lr,ltr): # lr=alpha, ltr=k
_w0=w0
_w1=w1
eps=0.1
for i in range(1,ltr):
grad_w=grad_loss(x,t,_w0,_w1)
_w0=_w0-lr*grad_w[0]
_w1=_w1-lr*grad_w[1]
if(max(np.absolute(grad_w))<eps):
break
return _w0,_w1
w0=1.0
w1=1.0
lr=0.001
ltr=1000
w0_opt,w1_opt=grad_descent(x,t,w0,w1,lr,ltr)
MAX(절대값(∇J) < 0.1 을 만족할 때까지 ∇J구하기를 Itr번 반복하는 코드입니다.
위를 만족하면 기울기가 0이랑 가장 비슷한 ∇J값을 구한 것이 됩니다!
// MAX함수를 이용한 이유는 D_w0와 D_w1 모두 0에 가깝도록 하기 위함 (∇J(0.2,0.98)보다는 ∇J(0.99,0.98)이 더 가까움)
grad_w는∇J, lr은 α(alpha)이고 _w0은 w0[1.0], _w1은 w1[1.0]으로 초기화되며 계속 업데이트됩니다.
_w0= _w0- lr * grad_w[0]는 w0(k+1) = w0(k) – α(D_w0)와 같습니다.
_w1= _w1- lr * grad_w[1]는 w1(k+1) = w1(k) – α(D_w1)와 같습니다.
grad_w(∇J)는 현재 w0와 w1을 기준으로 업데이트되니 grad_loss(x,t,_w0,_w1)를 계속 호출하며 업데이트됩니다.
최적의 grad_w(∇J)를 구했으면 그 때의 _w0[w0(k)]와 _w1[w1(k)]을 리턴합니다.
def show_line(x,t,w0,w1):
# true-dot
plt.plot(x,t,'o')
# model - line
y=w0*x+w1
plt.plot(x,y,color='red',linewidth=4)
w0_opt,w1_opt=grad_descent(x,t,w0,w1,lr,ltr)
print('W={0:.3F},{1:.3F}'.format(w0_opt,w1_opt))
show_line(x,t,w0_opt,w1_opt)
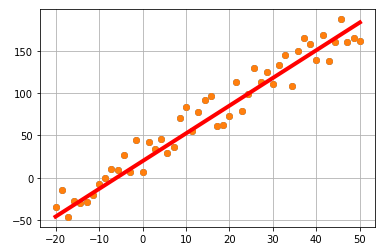
최적의 w0와 w1을 이용해서 선형 모델을 그려 보았습니다.
선형 모델에 필요한 x,t값들은 아래와 같은 방식으로 구현했습니다.
1. (y=3x+5)의 전처리 선형 모델을 미리 만들고 그 때의 x값들을 50개 생성한 뒤 y값들을 계산합니다,
2. t는 y에 랜덤 값을 더하는 방식으로 구합니다.
def targetfunc(x):
return 3*x+5
# x와 y구하기
x=np.linspace(-20,50,50) # x는 -20에서 50까지 50개 생성
fx=targetfunc(x)
# y를 기준으로 t구하기
np.random.seed(1) # 시드 고정
t=fx+50*np.random.rand(len(x)) # 랜덤값 50개로 y값(참값) 얻음
그렇다면 앞으로 최적화할 때 항상 이런 방식을 사용해야 될까요?
정답은 아닙니다.
사이킷런에는 최적화를 해주는 함수를 제공합니다.
minimize라는 함수에 (loss function, w의 초기값, 입력과 출력의 목표치)를 제공하면 최적화된 w들을 얻을 수 있습니다.
아래 코드를 실행하면 똑같은 실행 결과가 나옵니다!
import numpy as np
import matplotlib.pylab as plt
def targetfunc(x):
return 3*x+5
# x와 y구하기
x=np.linspace(-20,50,50) # x는 -20에서 50까지 50개 생성
fx=targetfunc(x)
# y를 기준으로 t구하기
np.random.seed(1) # 시드 고정
t=fx+50*np.random.rand(len(x)) # 랜덤값 50개로 y값(참값) 얻음
from scipy.optimize import minimize
# loss function(mse) 구하기
# val에 mse를 구하기 위한 값들이 누적해서 더해짐
def loss_mse(w,x,t):
y=w[0]+w[1]*x
val=0.0
for n in range(len(x)):
val=val+np.square(t[n]-y[n])
val=val/x.shape[0]
return val
wc=np.array([1.0,1.0])
_w=minimize(loss_mse,wc,args=(x,t)) # loss function, w의 초기값, 입력과 출력의 목표치
print(_w.x) # w0,w1
ft=np.array([[1.,xval] for xval in x]) # 행렬 형태 만들기
pred=np.dot(ft,_w.x) # 행렬 내적 계산하기
plt.plot(x,t,'o')
plt.plot(x,pred)
plt.grid()
plt.xlabel('x')
plt.ylabel('y')
plt.show()
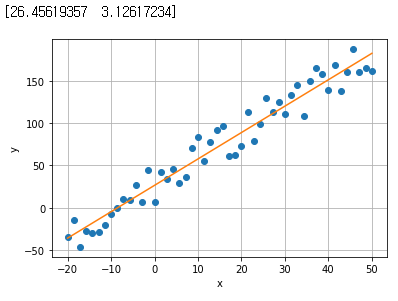
ft=np.array([[1.,xval] for xval in x]) # 벡터 형태 만들기 pred=np.dot(ft,_w.x) # 벡터 내적 계산하기
잠깐 위의 두 줄 코드만 살펴 보겠습니다.
(x는 입력 값 모음, _w.x는 최적화된 w값 모음, pred는 선형 모델의 예측 값(y) 모음)입니다.
먼저 x를 [1,x] 벡터로 표현합니다.
x가 (1,2,3)이면 벡터는 [1,1],[1,2],[1,3]이 됩니다.
이후 np.dot을 통해 _w.x(벡터)와 ft(벡터)를 내적합니다.
내적을 하면 선형 모델 식이 나오니 예측치를 구할 수 있게 됩니다!
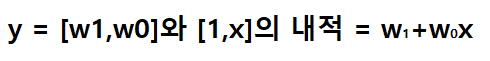
만약 [w1,w0]가 [5,3]이면,
pred[0] = [5,3] º [1,1] = 8
pred[1] = [5,3] º [1,2] = 11
pred[2] = [5,3] º [1,3] = 14
가 됩니다!
지금까지 입력값이 하나인 단순 선형 회귀를 알아 보았습니다.
만약 입력값(x)가 여러 개인 다중 선형 회귀일 경우 아래의 형태를 지닙니다!

오버피팅을 줄이기 위한 규제
이번에는 LM을 만들 때 오버피팅을 줄이는 방법을 알아 보겠습니다!
먼저 릿지 회귀입니다!
오버피팅을 줄이기 위해서 L2norm 규제를 합니다!
λ(lambda)는 α와 같습니다.
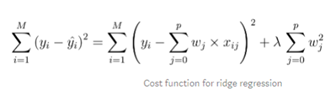
ridge10=Ridge(alpha=10).fit(X_train,y_train) # 릿지에서 람다가 10 <규제를 많이 한다는 의미> -> 일반화 많이 함
print("훈련 세트 점수:{:.2f}".format(ridge10.score(X_train,y_train)))
print("테스트 세트 점수:{:.2f}".format(ridge10.score(X_test,y_test))) #score함수가 알아서 시험 봐줌

람다 값이 크면 규제를 많이 합니다.
즉 오버피팅을 줄이고 일반화를 늘립니다.
-> [훈련 세트 점수]가 낮아 집니다.
-> [훈련 세트의 정확도와 시험 세트의 정확도 차이]가 적어 집니다. <0.14>
ridge01=Ridge(alpha=0.1).fit(X_train,y_train) # 릿지에서 람다가 0.1 <규제를 적게 한다는 의미> -> 일반화 적게 함
print("훈련 세트 점수:{:.2f}".format(ridge01.score(X_train,y_train)))
print("테스트 세트 점수:{:.2f}".format(ridge01.score(X_test,y_test))) #score함수가 알아서 시험 봐줌

람다 값이 작으면 규제를 적게 합니다.
즉 오버피팅이 발생할 수 있습니다.
-> [훈련 세트 점수]가 높아 집니다.
-> [훈련 세트의 정확도와 시험 세트의 정확도 차이]가 커집니다. <0.16>
Ridge로 규제한 결과 훈련 데이터가 많을수록 train과 test의 정확도 차이가 적어 집니다. (오버피팅 ↓)
규제하지 않았을 때는 train과 test의 정확도 차이가 점점 적어지긴 하나 규제한 만큼은 아닙니다.

다음은 라쏘 회귀입니다!
오버피팅을 줄이기 위해서 L1norm 규제를 합니다!
λ(lambda)는 α와 같습니다.
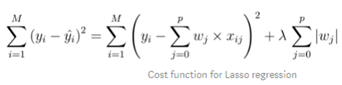
라쏘를 이용하면 feature를 선별할 수 있습니다!

한 샘플에 104개의 feature가 있는데 이 모든 feature가 회귀 분석(regression)하는데 영향을 줄까요?
그건 아닙니다. 라쏘에서 프로그래밍을 하다보면 coef(w:계수)가 0이 되는 경우도 생깁니다.
regression를 하려면 coef(w)가 필요한데 0이 나오니 올바른 regression이 나올 수 없습니다.
프로그램에서 coef가 0이면 feature는 사용하지 않는다고 처리합니다. 그래서 104개가 나와야 될 특성의 개수가 104개 미만이 나올 수도 있습니다.
정리하면, 릿치와 달리 라쏘를 이용하면 coef값이 0으로 딱 떨어지는 경우가 생깁니다.그래서 사용할 feature를 선별하기가 좋습니다!
lasso001=Lasso(alpha=0.01,max_iter=100000).fit(X_train,y_train) # 언더피팅 발생해서 alpha를 낮춰봄, 최적화할 때 반복을 100000으로 해봄
print("훈련 세트 점수:{:.2f}".format((lasso001).score(X_train,y_train)))
print("테스트 세트 점수:{:.2f}".format((lasso001).score(X_test,y_test)))
print("사용한 특성의 개수:",np.sum(lasso001.coef_!=0))

lasso00001=Lasso(alpha=0.0001,max_iter=100000).fit(X_train,y_train)
print("훈련 세트 점수:{:.2f}".format((lasso00001).score(X_train,y_train)))
print("테스트 세트 점수:{:.2f}".format((lasso00001).score(X_test,y_test)))
print("사용한 특성의 개수:",np.sum(lasso001.coef_!=0))

릿치와 마찬가지로 alpha(람다)를 높일수록 오버피팅이 적습니다. 즉 좋은 모델이 생깁니다.
마지막으로 람다와 Coef(w:계수)의 관계를 알아 보겠습니다.
이는 릿치와 라쏘의 람다 모두에 적용됩니다.
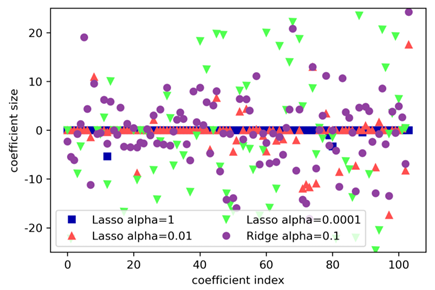
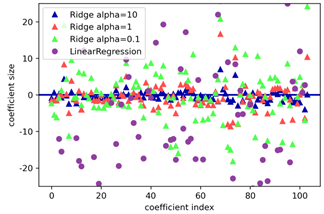
Alpha(람다)를 높이면 fature가 무엇이든 w가 모두 비슷한 수치를 보입니다. (범위가 줄어든다)
Alpha(람다)를 낮추면 feature에 따라 w가 변동이 큰 수치를 보입니다. (범위가 늘어난다)
람다에 따라 w도 달라진다는 점을 기억합시다!
감사합니다.
