인덱스: 색인 (파일의 레코드를 찾기 위해 필요)
<레코드 키 값, 레코드 주소(포인터)> 쌍 / 트리 구조로 되어 있음
인덱스의 종류
- 키에 따른 인덱스
– 기본 인덱스: 기본 키를 포함한 인덱스
– 보조 인덱스: 기본 인덱스 이외의 인덱스
- 파일 조직에 따른 인덱스
– 집중 인덱스(clustered): 데이터 레코드의 물리적 순서가 인덱스의 엔트리 순서와 동일하게 유지하도록 구성된 인덱스
– 비집중 인덱스: 집중 형태가 아닌 인덱스
- 데이터 범위에 따른 인덱스
– 밀집 인덱스: 데이터 레코드 하나에 대해 하나의 인덱스 엔트리가 만들어지는 인덱스. 역 인덱스라고도 함
– 희소 인덱스: 데이터 파일의 레코드 그룹 또는 데이터 블록에 하나의 엔트리가 만들어지는 인덱스
이원 탐색 트리

이원 탐색 트리의 검색
(K는 검색할 키 값, Ki는 노드가 가지는 키 값)
K=Ki: 노드 Ni가 원하는 노드
K<Ki: Ni의 왼쪽 서브 트리를 검색
K>Ki: Ni의 오른쪽 서브 트리를 검색
이원 탐색 트리의 삽입
(K는 삽입할 키 값, Ki는 노드가 가지는 키 값)
트리가 공백: 루트 노드에 삽입
K=Ki: 트리에 같은 키 값이 존재하므로 삽입을 거부
K<Ki: Ni의 왼쪽 서브 트리로 이동하여 계속 탐색
K>Ki: Ni의 오른쪽 서브 트리로 이동하여 계속 탐색
(리프 노드에만 삽입됨 / 중간에 삽입 안 됨)
이원 탐색 트리의 삭제
- 자식이 없는 리프 노드의 삭제
-> 단순히 그 노드를 삭제

- 자식이 하나인 노드의 삭제
-> 삭제되는 노드 자리에 자식의 자식 노드를 위치

- 자식이 둘 이상인 노드의 삭제
-> 왼쪽 서브트리에서 제일 큰 키(값) or 오른쪽 서브트리에서 제일 작은 키(값)로 대체,
->해당 서브트리에서 대체 노드를 삭제
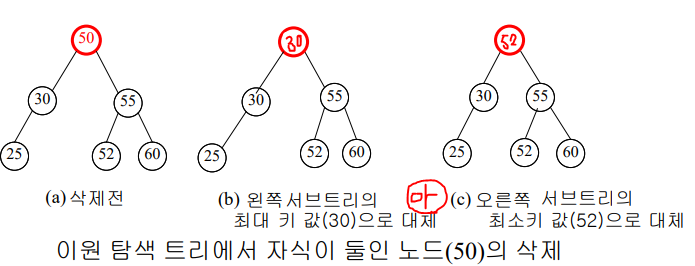
이원 탐색 트리의 성능
편향 이원 탐색 트리일 경우: 최악 <균형이 없으니 노드를 모두 조사해야됨>
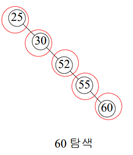
(최악의 경우) 탐색 시간: n번의 노드 탐색
높이를 최대한 낮게 만들어야 좋음!
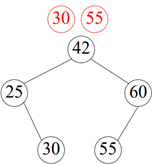
< 이 트리의 경우 높이가 3이니까 최대 3번을 거쳐서 찾게 됨 >
우수한 성능이 되는 조건은?
1. 자주 접근되는 노드는 루트에 가장 가깝게 유지함
2. 트리가 균형 트리가 되도록 해서 높이를 낮춤
이원 탐색 트리의 단점
1. 삽입, 삭제 후 효율적 접근을 위한 균형 유지가 힘듦
2. 작은 분기율에 따른 긴 탐색 경로와 검색 시간
(한 번에 분기가 2번 되니까 O(log2n)의 높이 가짐 -> O(log2n)의 탐색 시간)
(만약 분기가 10번되면 O(log10n)의 높이를 가져서 더 이득봤음)
AVL 트리 (높이 균형 이원 탐색 트리)
오른쪽 서브트리와 왼쪽서브트리의 높이 차가 1이하인 이원탐색트리
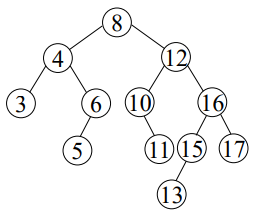
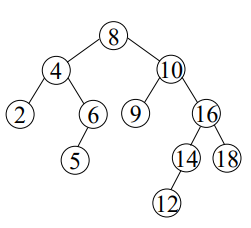
N(10)을 루트로 가지는 서브트리가 문제됨 (높이 차이2)
AVL 트리(높이 균형 이원 탐색 트리)의 검색과 삽입
검색: O(logn) – 일반 이원 탐색 트리의 검색 연산과 평균적으로 동일
삽입: 불균형이 탐지된 가장 가까운 조상 노드의 균형 인수를 +-1이하로 재균형 시켜야 함
(AVL 트리에서 불균형이란 균형인수가 1,-1이 아닐 때를 의미함)

노드 위에 써 있는건 균형인수: (왼쪽자식 수 – 오른쪽 자식 수)
(키 값이 8인 노드가 불균형이 탐지된 가장 가까운 조상)
X: 불균형으로 판명된 노드 <가장 가까운 불균형 노드 기준으로 생각>

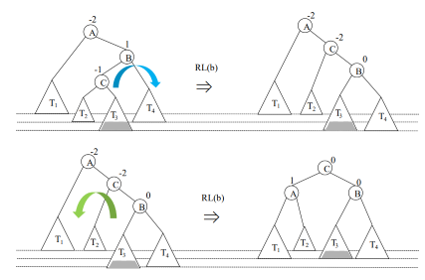
회전 (불균형 해결)
-단순회전: 한 번만 회전함, LL과 RR일 때
-이중회전: 두 번 회전함, LR과 RL일 때
(1) LL일 때 ->LL회전 진행
: x(5) 기준으로 [왼쪽->오른쪽] 회전
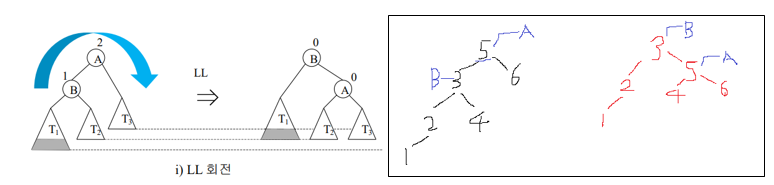
(2) RR일 때 ->RR회전 진행
: x(5) 기준으로 [오른쪽->왼쪽] 회전

(3) LR일 때 ->LR회전 진행
: x의 왼쪽 자식(2) 기준으로 [오른쪽->왼쪽] 회전, x(5) 기준으로 [왼쪽->오른쪽] 회전

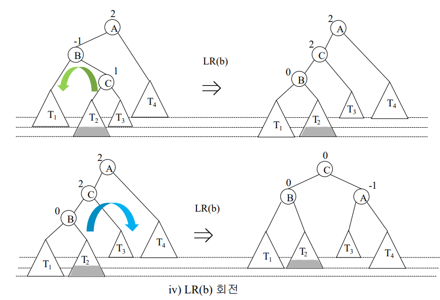
(4) RL일 때 ->RL회전 진행
: x의 오른쪽 자식(7) 기준으로 [왼쪽->오른쪽] 회전, x(5) 기준으로 [오른쪽->왼쪽] 회전
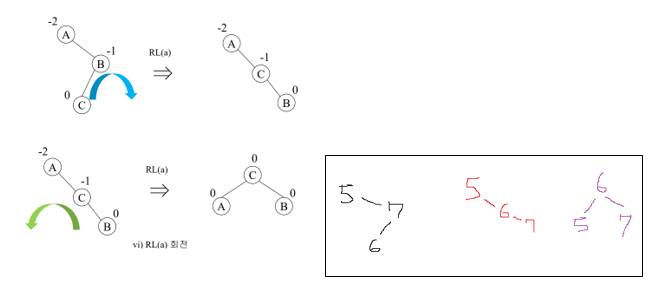
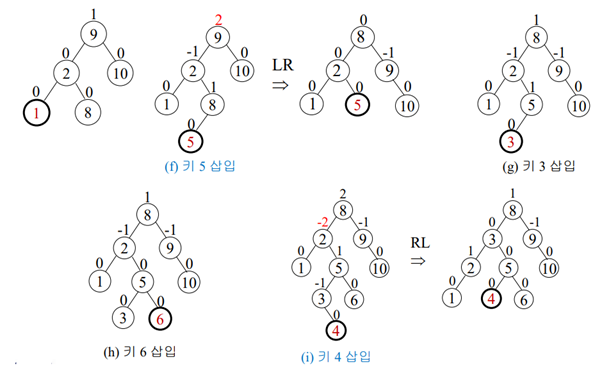
삽입-회전 연산을 이용해서 AVL 트리를 구축하기
(8,9,10,2,1,5,3,6,4,7,11,12) 삽입

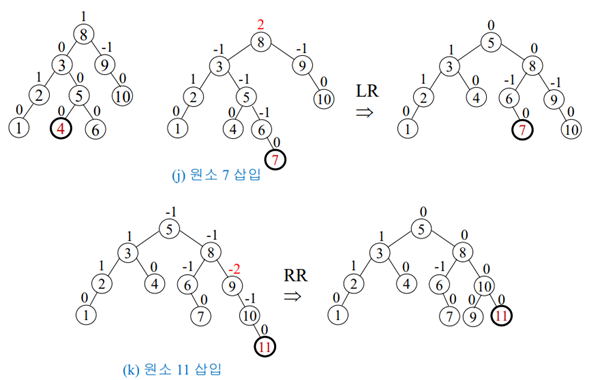
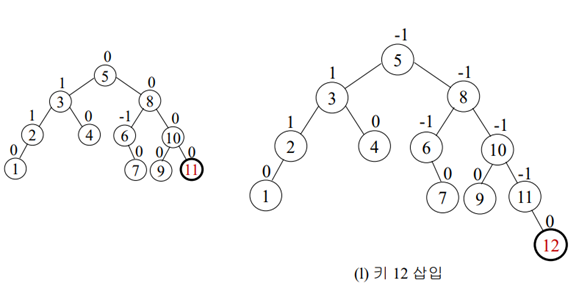
B트리(완전 균형 이진 탐색 트리)와 AVL트리(높이 균형 이진 탐색 트리)의 비교
- AVL트리의 탐색 시간이 더 길다. O(1.4 logn)이 걸림, B트리는 O(logn)
- 완전 균형 이진 탐색 트리는 변경시 전체 재균형 작업이 필요해서 더 복잡함
AVL 트리는 메인 메모리에 거주하는 내부 구조로써 트리 크기가 너무 커서 메인 메모리에 구축할 수 없을 수도 있음
- 균형 M-원 탐색 트리를 이용해야됨!
M원 탐색 트리
한 노드에 m-1개 키 값을 저장하는 m-원 탐색 트리
장점: 트리의 높이가 감소 (특정 노드의 탐색 시간 감소)
단점: 삽입,삭제 시 트리의 균형 유지 위해 복잡한 연산 필요

3원 탐색 트리
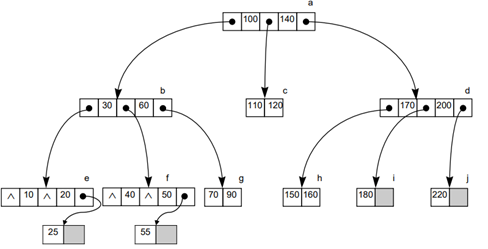
- 높이 h일 때 최대 키 값 n의 개수? // 루트 노드를 높이 1이라고 가정
: (m-1)*(m0+m1+…+mh-1) = mh-1개
ex) 높이 3인 노드의 개수 = m2-1= 3
- 최소 높이 h= ceil(logm(n+1)), 시간복잡도: O(logm(n+1))
B트리
완전 균형된 m-원 탐색 트리 : 가장 많이 사용되는 인덱스 방법

B트리의 장점
: 각 노드의 반 이상 채워져서 저장 장치를 효율적으로 사용 (3원일 때 자식 노드의 키는 적어도 1개 들어감(자식 노드를 가리켜야 되니 노드의 반 이상이 채워질 수밖에 없음 -> 저장 장치를 효율적으로 사용하게 됨),
삽입, 삭제 뒤에도 완전 높이 균형 상태 유지(m원 탐색 트리는 자식 노드가 없는 경우가 있어서 레벨 균형이 안 되지만, b트리는 항상 키 1개 이상인 자식이 있어서 레벨 균형이 됨)
3차 B트리

B트리의 삽입
여유 공간이 있는 경우: 단순히 순서에 맞게 삽입
여유 공간이 없는 경우: overflow, split 발생
1. 해당 노드를 두 개의 노드로 분할 (중간 값을 제외하고 작은 값과 큰 값으로 분할)
2. 중간 값은 부모 노드로 올라감
2-1. 부모 노드에 여유 공간이 있는 경우 단순히 순서에 맞게 삽입함
2-2. 부모 노드에 여유 공간이 없는 경우(overflow) 다시 분할(split)진행, 중간 값은 부모로 올라감
< overflow 발생 시 위와 같은 split 작업을 반복 >
< 루트 노드까지 올라갔는데 overflow가 발생한 경우 루트 노드를 분할 후 루트의 루트에 중간값을 넣음 -> 트리의 레벨이 올라감 >
(앞의 B트리에 새로운 키 값 22,41,59,57,54,33,75,124,122,123 삽입)
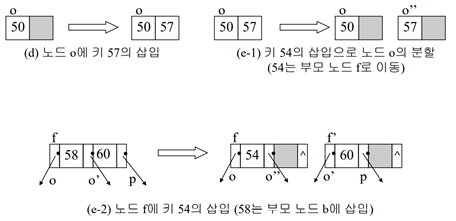
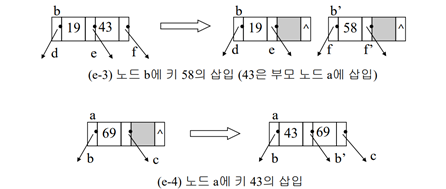
-> 33~122도 마찬가지로 진행, 123은 삽입 시 트리의 레벨이 증가됨

< 최종 결과 >
B트리의 삭제
<처음 시행>
잎 노드- 그냥 삭제
내부 노드- 후행키(오른쪽 서브트리 중 가장 작은 노드의 키)와 교환 -> 후행키 값은 삭제
< 처음 시행 후 문제(underflow) 발생 >

-> 재분배가 가능하면 재분배하고, 안 되면 합병하고
삭제: 58,7,60,20,15
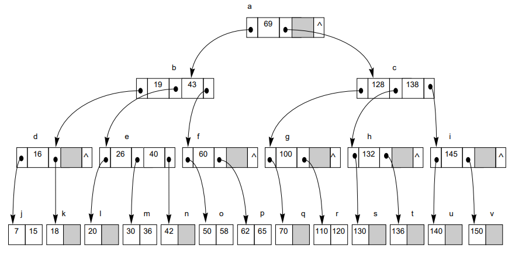
Ex) 58,7,60 삭제 (처음 시행에서 끝나는 경우)
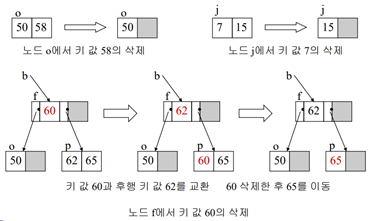
Ex) 20 삭제 (재분배:redistribution)

20을 삭제하니 l노드에서 언더플로우 발생 -> 형제 노드(m)를 이용해서 재분배 -> 재분배할 때는 ‘회전’을 이용함
Ex) 15 삭제(합병:merge)
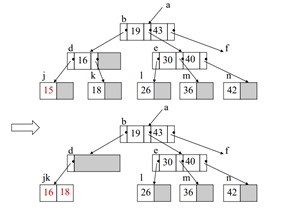
15를 없애니까 j노드에서 언더플로우 발생 -> 형제 노드(k:18)을 빌려오려고 하니 형제 노드(k)가 언더플로우 발생 -> 재분배하지 않고 부모노드와 형제노드가 합병됨
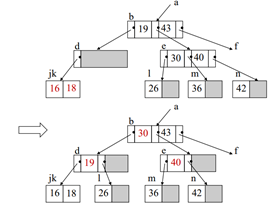
합병되면서 d노드가 언더플로우가 됨 -> 형제 노드(c)를 빌려옴 -> ‘회전’을 이용해서 재분배
트라이
키를 구성하는 문자나 숫자의 순서로 키 값을 표현한 구조 (m-진 트리라고 함)
차수m: 키 값을 표현하기 위해 사용하는 문자의 수, 즉 기수
10진 숫자: 기수가 10이므로 m=10, 영문자: m=26
트라이의 높이 = 키 필드의 길이
<중복 아이디 조회에 사용>
( 트라이-10진트리의 탐색과 삽입,삭제 )

탐색 끝은 언제인가?
리프노드이거나(성공) 중간에 키 값이 없을 때(실패)
키 필드의 길이(10진수일 때는 자릿수) = 트라이의 높이 (위 이미지에서는 3)
최대 탐색 비용 <= 키 필드의 길이
장점: 균일한 탐색 시간과 없는 키에 대한 빠른 탐색
삽입
리프 노드에 새 레코드의 주소나 마크를 삽입
리프 노드 없을 때: 새 리프 노드 생성
(분열이나 병합은 없음)
삭제
노드와 원소들을 찾아서 널 값으로 변경
노드의 원소 값들이 모두 널이면 모두 삭제
인덱스된 순차 파일의 구조
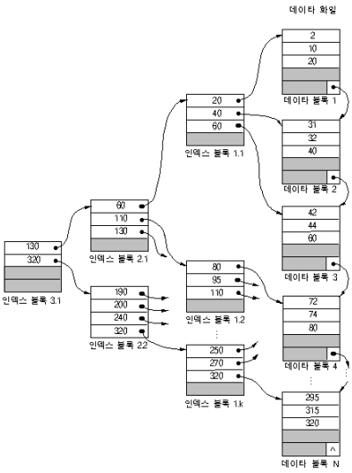
인덱스(B트리)와 순차 데이터 파일(데이터 블록)을 합친 개념[실제 데이터는 데이터 블록에 위치함]
: 키 값에 따라 정렬된 레코드를 순차적으로 접근하거나(일괄 처리) 키 값에 따라 직접 접근하는 경우(대화식 처리)에 사용
마스터 인덱스: (루트 노드) 최상위 레벨의 인덱스 블록
인덱스 엔트리의 구성: 최대키 값,포인터
(130보다 작거나 같은 것들, 320보다 작거나 같은 것들이 각각 서브 트리 형태로 만들어짐)
인덱스된 순차파일 개념을 이용해서 실제 사용되는 구조: B+ 트리
목적: 순차 탐색의 성능 향상 (B트리의 순차 탐색 보완)
인덱스 세트: 리프 이외의 노드 / 구조:(키 값, 리프 노드까지 가는 경로)
순차 세트: 리프 노드 / 구조:(키 값, 데이터 레코드의 주소)
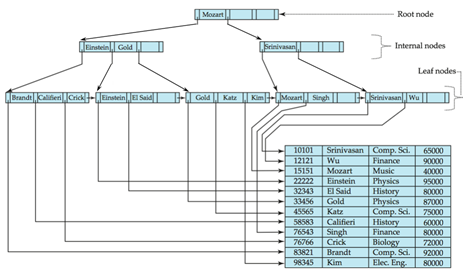
B트리와 비교하기
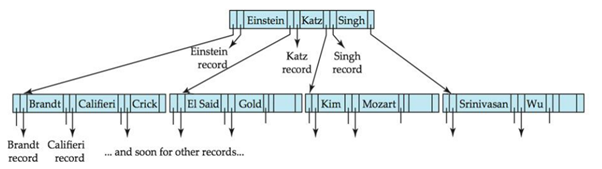
내부노드나 리프노드나 모두 똑같은 구조, 똑같은 역할을 함
(포인터1,키1 레코드,키1 이름, 포인터2,키2 레코드,키2 이름,포인터3,키3 레코드,키3 이름,포인터4)
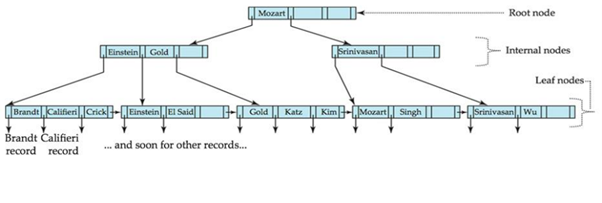
루트나 내부노드는 리프 노드를 찾아가는 경로를 나타냄, 리프 노드가 실제 레코드를 가짐
(노드마다 역할이 다름)
B+트리에서 키 값의 삽입
차이: 리프 노드 분할 시 중간 키 값은 그대로 두고 복사본이 부모 인덱스 노드로 올라감
(모든 데이터가 리프에 있어야 되니까)
- 내부 노드 분할 시 B트리와 똑같이 진행한다.
3차 B+트리에서의 삽입

<15,69,110,90,20,120,40,125를 삽입>
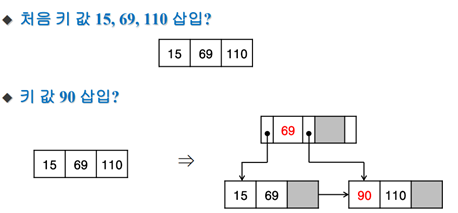
15,69 / 90,110으로 분할(B트리면 중간 값을 제외하고 분할하지만 여기서는 다름) -> 69의 복사본이 부모로 감(B트리면 원본이 감)

단순히 20,120 삽입

15,20 / 40,69로 분할 -> 20의 복사본이 부모로 감 -> 40은 제 위치에 삽입
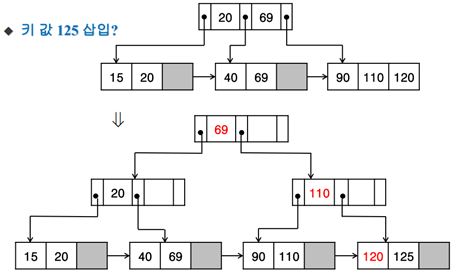
90,110 / 120,125로 분할 -> 110의 복사본이 부모로 가려는데 꽉 참 ->
[B트리랑 똑같이 진행] 20(작은 수)과 110(큰 수)으로 분할, 69(가운데 수)는 부모로 감
B+트리에서 키 값의 삭제
차이: 리프 노드에서만 삭제

리프노드 Underflow: ceil[m/2]=2보다 작을 경우
내부노드 Underflow: ceil[m/2]-1=1보다 작을 경우
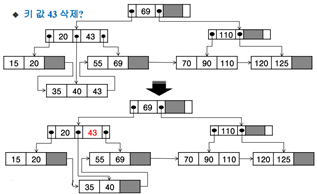
리프 노드의 43을 찾음 -> 삭제

리프 노드의 125를 찾음 -> 리프 노드에서 삭제 -> 언더플로우 발생(키가 1개) -> 형제 노드로 재분배 (회전을 이용, 부모에 위치한 110은 회전해서 오른쪽 자식으로 가고 원본은 삭제, 왼쪽 자식에 위치한 90은 복사본이 부모로 감)
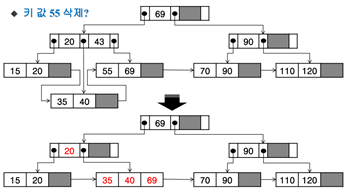
리프 노드의 55를 찾음 -> 리프 노드에서 삭제 -> 언더플로우 발생(키가1개) -> 재분배하려니 형제 노드에서 언더플로우 발생 -> 형제 노드의 키 값과 합병 [35,40,69] -> 43키 값이 문제가 생김(경로가 안 맞아짐) -> 43은 이전에 지워진 값임 -> 그냥 삭제

장점: B트리같이 노드에서 레코드 포인터를 저장하지 않으니, 그 자리에 키 값과 Child 포인터가 더 들어가면 레벨이 낮아질 수 있음 (위 예시는 키 값이 더 들어가지는 않았음)

