최대 부분 배열 합을 구하는 방법은 여러 가지입니다

1. 시간복잡도가 O(n^3)인 방법
2. 시간복잡도가 O(n^2)인 방법
3. 시간복잡도가 O(nlogn)인 방법
4. 시간복잡도가 O(n)인 방법

위 네 가지 방법을 제공합니다.

※ 단 아래 알고리즘은 최대 부분 배열 합의 최솟값이 0이상임을 보장합니다.

알고리즘1 – 시간복잡도 O(n^3)

type MaxSubarray1(type A[], type n) {
	type MaxSum, ThisSum;
	type i, j, k;

	MaxSum = 0;
	for (i = 0; i < n; i++) {
		for (j = i; j < n; j++) {
			ThisSum = 0;
			for (k = i; k <= j; k++)
				ThisSum = ThisSum + A[k];
			MaxSum = max(MaxSum, ThisSum);
		}
	}
	return MaxSum;
}

모든 경우의 수를 구하는 가장 일반적인 방법입니다.

배열의 크기가 n이고 부분 배열이 [i,j]일 때, i와 j를 구하는 반복문 2개를 이용합니다. (0 <= i,j <= n-1)
변수k로 범위(i~j)를 지정 후 안쪽 반복문에서 부분배열 합을 구합니다. (A[i]+….+A[j] 구하기)
MaxSum에는 max함수를 이용해서 최대 부분 배열 합을 저장합니다. (부분배열 합을 구할 때마다 MaxSum은 업데이트)

알고리즘2 – 시간복잡도 O(n^2)

type MaxSubarray2(type A[], type n) {
	type MaxSum, ThisSum;
	type i, j;

	MaxSum = 0;
	for (i = 0; i < n; i++) {
		ThisSum = 0;
		for (j = i; j < n; j++) {
			ThisSum = ThisSum + A[j];
			MaxSum = max(MaxSum, ThisSum);
		}
	}
	return MaxSum;
}

알고리즘1에서 불필요한 코드를 제거한 방법입니다.

배열의 크기가 n이고 부분 배열이 [i,j]일 때, i와 j를 구하는 반복문 2개를 이용합니다. (0 <= i,j <= n-1)
구해진 i와 j로 부분배열 합을 구합니다. 합을 구한 뒤 바로 MaxSum을 업데이트합니다.

ex) 기존 ThisSum(A[1,2])에 A[3]를 더해서 업데이트하고 바로 MaxSum(A[0,0]~A[1,2]중 가장 큰 값)과 비교한다. -> 업데이트된 ThisSum(A[1,3])이 MaxSum보다 크면 MaxSum업데이트!

알고리즘3 – 시간복잡도 O(nlogn)

type MaxSubarray3(type A[], type Left, type Right) {
	type MaxSum, MaxLeft, MaxRight, MaxCenter;
	type MaxCenterL, MaxCenterR, ThisSum;
	type Center, i;

	if (Left == Right) { // 배열 원소가 한 개인 경우 
		if (A[Left] > 0)
			return A[Left];
		else
			return 0;
	}

	Center = (Left + Right) / 2;
	MaxLeft = MaxSubarray3(A, Left, Center);
	MaxRight = MaxSubarray3(A, Center + 1, Right);

	MaxCenterL = 0;
	ThisSum = 0;
	for (i = Center; i >= Left; i--) {
		ThisSum = ThisSum + A[i];
		MaxCenterL = max(MaxCenterL, ThisSum);
	}

	MaxCenterR = 0;
	ThisSum = 0;
	for (i = Center + 1; i <= Right; i++) {
		ThisSum = ThisSum + A[i];
		MaxCenterR = max(MaxCenterR, ThisSum);
	}

	MaxCenter = MaxCenterL + MaxCenterR;

	MaxSum = max(max(MaxLeft, MaxRight), MaxCenter);
	return MaxSum;
}

실행 시간을 확실하게 줄이는 ‘분할정복법’을 이용한 코드입니다.

먼저 배열을 오른쪽 Part와 왼쪽 Part로 나눕니다.
이를 배열L, 배열R이라고 하겠습니다.

① 배열L에서 최대 부분 배열 합 찾기 (MaxLeft)
② 배열R에서 최대 부분 배열 합 찾기 (MaxRight)
③ 겹치는 부분에서 최대 부분 배열 합 찾기 (MaxCenter)

과정을 진행한 뒤 ①,②,③ 중 가장 큰 수를 찾으면 해결됩니다.

단, ③ 겹치는 부분에서 ‘최대 부분배열 합’을 찾을 때 아래와 같은 방식으로 찾으면 시간복잡도가 O(n^2)이 되니 아이디어가 필요합니다.

해답은 오른쪽 ‘최대 부분 배열 합’에 왼쪽 ‘최대 부분 배열 합’을 합쳐서 겹친 부분 배열 합을 구하는 것입니다.

오른쪽 배열에서 구한 최대 합(MaxCenterL)과 왼쪽 부분 배열에서 구한 최대 합(MaxCenterR)을 더하면 겹친 부분 배열에서 구한 최대 합(MaxCenter)과 같기 때문입니다!
물론 이 때의 오른쪽, 왼쪽 배열은 Center 원소를 포함한 상태여야 됩니다!

MaxCenter를 구하기 위해 왼쪽 부분은 처리할 때는 left에서 Center까지 진행합니다.
ex) n이 8일 때 left는 0, Center는 3 -> [0,3], [1,3], [2,3], [3,3]는 4개

MaxCenter를 구하기 위해 오른쪽 부분을 처리할 때는 Center+1에서 Right까지 진행합니다.
ex) n이 8일 때 Center+1는 4, right는 7 -> [4,4], [4,5], [4,6], [4,7]는 4개

그리고 합치는 연산을 α개라고 할 때, 총 연산의 수는 (2/n+ 2/n + α)개가 됩니다.
그리고 이를 자세하게 시간복잡도로 따져보면 O(nlogn)이라고 합니다.

MaxCenter를 구하기 위해 배열L과 R에서 ‘최대 부분 배열 합’을 구하는 방법은 [알고리즘2]와 같은 논리입니다.

MaxCenterL = 0;
ThisSum = 0;
for (i = Center; i >= Left; i--) {
ThisSum = ThisSum + A[i];
MaxCenterL = max(MaxCenterL, ThisSum);
}

MaxCenterR = 0;
ThisSum = 0;
for (i = Center + 1; i <= Right; i++) {
    ThisSum = ThisSum + A[i];
    MaxCenterR = max(MaxCenterR, ThisSum);
}

MaxCenter = MaxCenterL + MaxCenterR;

그렇다면 ①(MaxLeft)과 ②(MaxRight)는 어떻게 구하면 될까요?

MaxCenter를 구하는 방법을 그대로 이용하면 시간복잡도를 유지할 수 있습니다!

①(MaxLeft)

MaxLeft를 구하는 방법은 (left~center)범위에서 구할 수 있는 MaxCenter중 최댓값을 찾는 것입니다!
예를 들어 배열이 [1,2,3,4,5,6,7,8]이라고 가정합시다.
MaxLeft를 구하기 위해서 [1,2,3,4]만 따져 봅니다.
[1,2,3,4]에서 구할 수 있는 MaxCenter는 범위를 반으로 나눠 가며 조사합니다.
[1], [2], [3], [4], [1,2], [3,4], [1,2,3,4]
이런 식으로 말이죠!
이후 위 7가지 경우에서 각각 구한 MaxCenter중 최댓값을 구하면 MaxLeft가 완성됩니다!
단 배열 원소가 한 개인 경우는 양수일 때 해당 값을 출력하면 됩니다. (Max의 최솟값은 0이기 때문에 음수는 인정x)

②(MaxRight)

MaxRight를 구하는 방법은 (center+1~right)범위에서 구할 수 있는 MaxCenter중 최댓값을 찾는 것입니다!
예를 들어 배열이 [1,2,3,4,5,6,7,8]이라고 가정합시다.
MaxRight를 구하기 위해서 [5,6,7,8]만 따져 봅니다.
[5,6,7,8]에서 구할 수 있는 MaxCenter는 범위를 반으로 나눠 가며 조사합니다.
[5], [6], [7], [8], [5,6], [7,8], [5,6,7,8]
이런 식으로 말이죠!
이후 위 7가지 경우에서 각각 구한 MaxCenter중 최댓값을 구하면 MaxRight가 완성됩니다!
단 배열 원소가 한 개인 경우는 양수일 때 해당 값을 출력하면 됩니다. (Max의 최솟값은 0이기 때문에 음수는 인정x)

두 방식 모두 범위를 반으로 나눠가며 조사하는 작업을 반복합니다.
고로 순환 알고리즘이 쓰인 것입니다!

순환 구조에 의해서 ①(MaxLeft)과 ②(MaxRight)를 모두 구한 뒤 left와 right는 맨 처음 호출됐을 때의 값과 같습니다.
이후 ③(MaxCenter)를 구하면 ①,②,③을 모두 구하게 됩니다!

마지막으로 Max(①,②,③)을 반환하며 프로그램은 종료됩니다.

알고리즘4 – 시간복잡도 O(n)

type MaxSubarray4(type A[], type n) {
	int MaxSum, ThisSum;
	int k;

	MaxSum = 0;
	ThisSum = 0;
	for (k = 0; k < n; k++) {
		ThisSum = max(ThisSum + A[k], 0);
		MaxSum = max(MaxSum, ThisSum);
	}
	return MaxSum;
}

마지막으로 ‘동적계획법’을 사용한 코드입니다.

이 수식이 곧 아이디어입니다!

‘S[k]: 부분배열의 오른쪽 끝이 A[k]인 최대 부분 배열 합’의 형태는
⑴ 0 (길이가 0)
⑵ A[k-1]를 오른쪽 끝으로 갖는 ‘최대 부분 배열 합’에 A[k]를 더한 것 (길이가 1 이상)
두 가지라는 의미입니다!

배열을 K번째에서 끊고 K번째 원소를 기준으로 왼쪽으로 원소를 추가해가며 생각해봅시다.

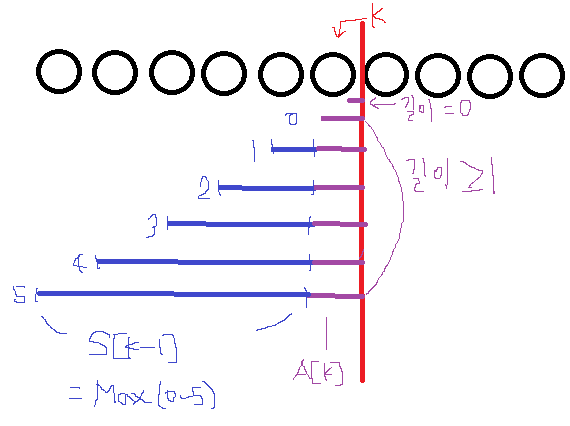
길이가 하나 이상이면 A[k]는 무조건 포함한다고 생각하는 것입니다.
이 때 S[k]는 ‘A[k-1]를 오른쪽 끝으로 갖는 배열들 중 가장 큰 것(max(0~5))’ 즉 S[k-1]에 A[k]를 더한 것이 됩니다.

‘길이가 하나 이상이면 A[k]를 항상 가지고 있으니 나머지 것들 중 가장 큰 것이 제일 큰 것이다.’ 라는 논리입니다!

그렇다면 여기서 의문점이 생길 수 있습니다!
어떤 경우일 때 길이가 0인가?

이것은 S[k-1]+A[k]가 ‘가질 수 있는 최솟값(0)’ 보다 작거나 같을 때 취급합니다!
ex) 7 2 -10일 때 S[1]+A[2] = -1  ➜ 길이가 0  ➜ S[2] = 0

즉 A[k] <= – S[k-1]일 경우 길이가 0이라고 취급합니다!

위 작업들을 k=0부터 n-1까지 모두 해가며 S[k]들을 구할 때, 가장 큰 S[k]가 ‘최대 부분 배열 합’이 됩니다.

또한 S[k]들을 배열에 따로 저장하지 않고 ThisSum변수에 저장한 후 바로 MaxSum(s[0],…s[k-1]중 가장 큰 값)과 크기 비교를 하면 ‘공간복잡도’를 줄일 수 있습니다!

그렇게 해서 나온 코드는 아래와 같습니다!

for (k = 0; k < n; k++) {
		ThisSum = max(ThisSum + A[k], 0);
		MaxSum = max(MaxSum, ThisSum);
	}

반복문 한 번으로 원하는 실행 결과가 나오는 획기적인 아이디어입니다!

알고리즘4가 얼마나 대단한지 알아보기 위해 빅 데이터를 이용해서 그래프를 그려 보았습니다.

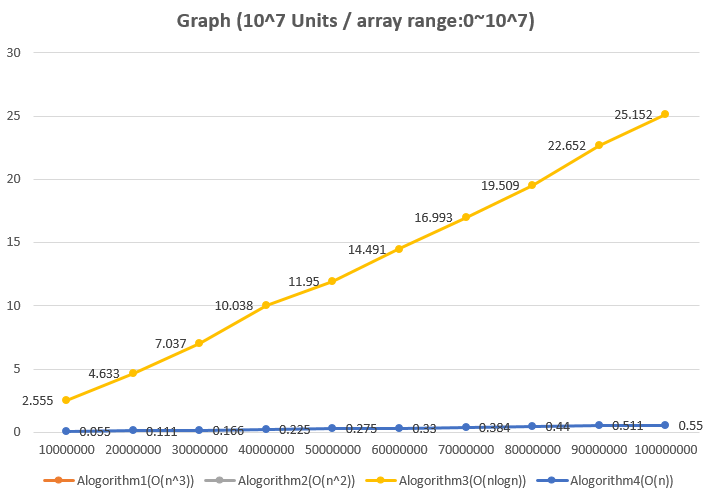
배열의 크기가 천 만인 것부터 일 억인 것까지 ‘최대 부분 배열 합’을 구하는 소요 시간 그래프입니다.

알고리즘1과 2같은 경우 30초를 초과해서 그래프에 나타나지 않습니다.

알고리즘3은 2.5초부터 25초까지 점점 소요 시간이 늘어나는 것을 확인할 수 있습니다.

알고리즘4도 소요 시간이 점점 늘어나지만 모두 1초 이내이므로 성능이 가장 우수합니다!

지금까지 ‘최대 부분 배열 합’ 알고리즘을 알아보았습니다.

이번 포스팅의 핵심은 알고리즘과 프로그램 성능간의 관계입니다.

좋은 프로그램을 만들기 위해 우수한 알고리즘을 구상하는 개발자가 됩시다! ^~^