K-NN : 새로운 데이터가 주어지면 [기존 데이터 중 가장 가까운 k개의 데이터와 비교해서] 새로운 데이터를 분류(예측)하는 알고리즘이다.

토마토가 새로운 사례로 들어왔을 때 , 토마토랑 가까운 (껍질 콩, 견과류, 포도, 오렌지)와 비교해서 가장 가까운 곳으로 분류한다.
거리 계산은 유클리드 거리 공식을 그대로 사용합니다.
P와 Q사이의 거리
Dist(p,q) = { Sigma(i=1 -> n) (pi-qi)^2 } ^(1/2)
n: p,q의 좌표 개수
ex) P(3,0), Q(2,1)
=> { (3-2)^2 + (0-1)^2 }^(1/2) = √ 2
아래의 연습 문제를 R로 해결해봅시다!

# 4행 2열, 데이터는 행(가로)으로 저장되게 a행렬을 만듦
a<-matrix(c(8,5,3,7,3,6,7,3),4,2,byrow = T)
# 각각의 행에 대해 유클리드 거리 공식을 적용하고 결과를 dist벡터에 담음
fun=function(x,y){
dist<-c()
for(i in 1:4){
dist[i]<-sqrt((a[i,1] - x)^2+(a[i,2] - y)^2)
}
return(dist)
}
dist<-fun(6,4)
dist
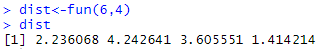
오렌지와 가장 거리가 가까우므로 토마토는 ‘과일’로 분류된다!
이제 본격적으로 K-NN을 알아 봅시다!
K-NN에서 K는 최적 이웃의 수를 의미합니다!-

왼쪽 이미지에서는 이웃이 하나이기 때문에, 검은 색 공은 파란 색 공으로 분류됩니다.
오른쪽 이미지처럼 이웃이 세 개면 다수결로 결정하되, 가중합이라는 것을 이용합니다.
- 거리가 가까운 이웃에 좀 더 가중치를 주어 class를 결정 (가중합)
- 거리(x)에 반비례하게 가중치를 줌 <거리 클수록 가중치 작음>
위 이미지는 가까운 원소가 파란 색이고, 파란 공이 많아서 문제가 되지 않습니다.
이는 거리가 가까운데 원소가 하나라서 그쪽으로 분류가 안 될 경우를 막기 위함입니다.
가중치는 다음과 같은 식으로 부여합니다.
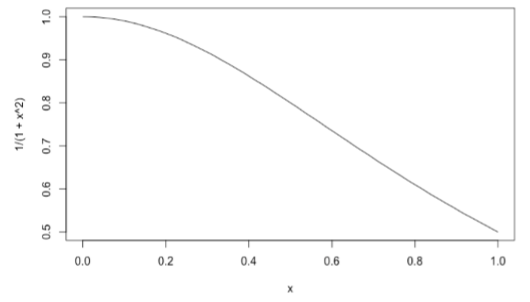
1/(1+x^2): 거리가 가까우면 가중치 비슷하게 주겠다. / 거리가 멀면 가중치 확연히 다르게 주겠다.
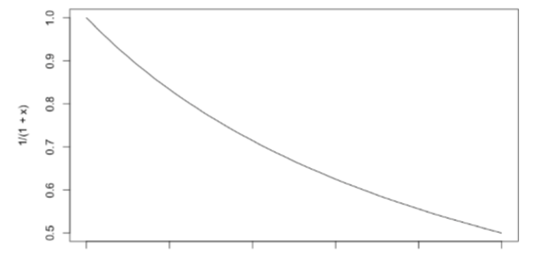
1/1+x, exp(-x): 거리가 가까우면 가중치 확연히 다르게 주겠다. /거리가 멀면 가중치 비슷하게 주겠다

이번에는 적절한 k를 선택해야 하는 이유를 알아 봅시다!
먼저 최적의 이웃을 찾게 되면, 그 이웃을 기준으로 경계선이 생깁니다.

위는 (K=1)일 때 경계선이고, 검정 색 공이 새로운 데이터입니다.
이 때 검정 공은 주황 공과 더 가까운데도 불구하고 경계선 안에 속해서 파란 공으로 분류됩니다.
이를 ‘과적합’이라고 합니다.
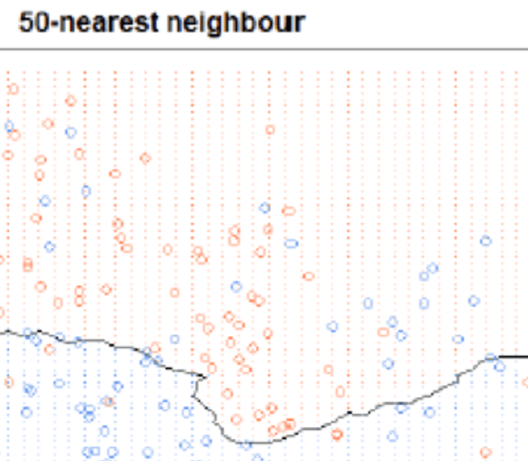
위는 (K=50)일 때 경계선입니다.
이웃이 많아서 경계는 그만큼 커지게 되고 위같은 현상이 발생합니다.
그 경계면이 기존 데이터도 침범하면, 기존 데이터까지 오분류될 수 있습니다.
이를 ‘Underfitting’이라고 합니다.
그렇다면 어떠한 방식으로 적절한 K를 찾을까요?
바로 GREEDY 알고리즘을 이용합니다.

위는 K수에 따른 오류율을 나타낸 그래프입니다.
K=3일 때가 최적(최저)의 오류일지, K가 5초과일 때 최적(최저)의 오류일지는 모릅니다.
그러나 모든 데이터에 대해 k를 조사하지 않고, 변곡점이 생기는 부분을 최적의 오류로 간주합니다.
한치 앞의 이익만 추구하는 Greedy 알고리즘입니다.
여기까지 knn에 대한 이론적인 부분을 알아 보았습니다.
마지막으로 실습 전 주의점을 설명하겠습니다.
거리 기반 알고리즘은 변수의 정규화가 필수적입니다.
정규화가 필요한 이유가 작성된 포스트:
https://shacoding.com/2019/10/20/mining-10%eb%8c%80-%eb%8d%b0%ec%9d%b4%ed%84%b0%eb%a5%bc-%ec%9d%b4%ec%9a%a9%ed%95%9c-%ed%81%b4%eb%9f%ac%ec%8a%a4%ed%84%b0%eb%a7%81-%ec%8b%a4%ec%8a%b5/

위는 변수의 정규화를 해서 모든 값을 [0,1]사이의 값으로 만드는 정규화 공식입니다.
다음에 ’KNN 실습’으로 찾아 뵙겠습니다!
