지도 학습 분류 방법 중 나이브 베이즈(NB)를 소개하겠습니다.

‘나이브 베이즈’는 통계학의 ‘베이즈 정리’를 이용한 분류 기법입니다.

아래는 베이즈 정리에 해당하는 식입니다.

교집합: P(A교B) = P(A,B) = P(B,A)
베이즈 정리: P(A|B) = P(B,A)/P(B) = P(B|A) x P(A)/P(B)
P(A): 사전확률, P(A|B): 사후확률, P(B|A): 우도

베이즈 정리 식에 대한 간단한 문제를 풀어 보겠습니다.
(출처. [머신러닝] 나이브 베이즈 (Naive Bayes) (tistory.com))

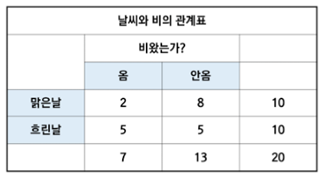
Q. 비가 올 확률, 비가 안 올 확률, 맑은 날인 확률, 비가 올 때 맑은 날일 확률, 맑은 날일 때 비가 올 확률을 구하시오.

P(비) = 7/20
P(비 안 옴)= 13/20
P(맑은 날) = 10/20
P(맑은 날|비)=P(비,맑은 날)/P(비)=2/20 / 7/20 = 2/7 (조건부 확률)
P(비|맑은 날)=P(비,맑은 날)/P(맑은 날) = 2/20 / 10/20 = 1/5 (조건부 확률)
P(맑은 날|비)=P(비|맑은 날)*P(맑은 날)/P(비) = 1/5 x 10/20 / 7/20 = 2/7 (베이즈 정리)
P(비|맑은 날)=P(맑은 날|비)*P(비)/P(맑은 날) = 2/7 x 7/20 / 10/20 = 1/5 (베이즈 정리)

이제 베이즈 정리로만 풀 수 있는 문제를 풀어 보겠습니다.

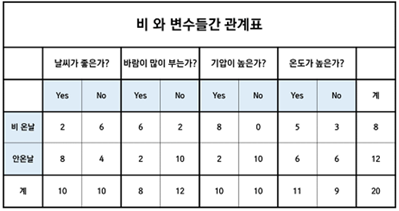
Q. 날씨가 좋고 바람이 안 불고 기압이 높고 온도가 낮을 때 비가 올 확률을 구하시오.

B=(날씨,~바람,기압,~온도)일 때, P(비|B)가 무엇인지 구하는 문제입니다.

이 문제를 단순하게 조건부 확률로 계산하기에는 자료가 미흡합니다.
P(비,B)를 구해야 되는데, B라는 많은 조건들을 만족하면서 비가 오는 것은 표에 나와있지 않습니다.

하지만 P(B)와 P(B|비)는 독립 사건임을 이용해서 구할 수 있을 것 같습니다.

(날씨),(바람),(기압),(온도)가 독립이고 독립일 때 교집합 문제는 곱하기로 변형해서 풀 수 있습니다.
따라서 P(B) = P(날씨) x P(~바람) x P(기압) x P(~온도)로 표현이 가능합니다.
이를 계산하면 p(B) = 10/20 x 12/20 x 10/20 x 9/20 = 0.06이 나옵니다.

같은 이치로 (비가 올 때 날씨), (비가 올 때 바람), (비가 올 때 기압), (비가 올 때 온도)도 독립입니다.
따라서 P(B|비) = P(날씨|비) x P(~바람|비) x P(기압|비) x P(~온도|비)로 표현이 가능합니다.
이를 계산하면 p(B|비)= 2/8 x 2/8 x 8/8 x 3/8 = 0.02이 나옵니다.

P(B)와 P(B|비)를 구하였으니 P(비|B)는 베이즈 정리로 해결이 가능합니다!

베이즈 정리에 의하면, P(비|B) = P(B|비) x P(비) / P(B)이기 때문에,
P(비|B) = 0.02 x (8/20) / 0.06 = 0.13이 나옵니다.

즉 정답은 13%가 됩니다.

이 문제에서 정답을 구하는 것은 크게 중요하지 않습니다.
중요한 것은 베이즈 정리의 필요성을 파악하는 것입니다.

P(A|B)를 구하는 것이 목적일 때, P(B|A)를 구하는 것이 상대적으로 더 쉽다면 베이즈 정리를 이용하면 됩니다!

이를 스팸 분류 문제로 생각하겠습니다.

‘money’문구를 포함하는 문자들이 주어졌을 때, 스팸 문자를 찾는 것이 쉬울까요?
스팸 문자들이 주어졌을 때, ‘money’문구를 포함하는 문자를 찾는 것이 쉬울까요?

당연히 단순 검색만으로 해결되는 후자가 더 쉽습니다.

그렇다면 (A: 스팸 문자, B: ‘money’문구를 포함하는 문자)일 때, P(B|A)를 구하기 더 쉽다는 것이 됩니다.
결국 P(A|B)는 P(B|A)와 베이즈 정리 식을 이용해서 구할 수 있습니다.

마지막으로, 이와 관련된 스팸 메일 분류 문제를 풀어 보겠습니다!

p(spam|money)를 구하려는데, p(money|spam)은 구하기 쉬우므로 이미 주어져 있습니다.
p(spam), p(money)도 이미 주어져 있습니다.
베이즈 정리 식에 그대로 대입하면 정답은 (2/5) x (30/100) / (50/100) = 24%가 됩니다!

다시 말하지만, 나이브 베이즈는 베이즈 정리를 이용한 분류 기법입니다!
아래는 나이브 베이즈의 특징입니다.

지금까지, 통계학에 근거한 좋은 분류 방법이 있다는 것을 소개해보았습니다.

나이브 베이즈 분류 코드를 끝으로 포스팅을 마칩니다.

감사합니다!

import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.naive_bayes import BernoulliNB
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from utilities import visualize_classifier

input_file='./data/data_multivar_nb.txt'
data=np.loadtxt(input_file, delimiter=',')
x, y = data[:,:-1], data[:,-1]
# x: 모든 행, 마지막 열 제외한 모든 열 가져오기
# y: 모든 행, 마지막 열 가져오기 (target열) 
print(data.shape)
print(x.shape)
print(y.shape)
print(x[0:5])
print(y[0:5])

x_train, x_test, y_train, y_test = train_test_split(x,y,random_state=0)

# 연속적인 데이터에 사용
classifier = GaussianNB()

# 텍스트 데이터에 사용
# classifier = BernoullliNB()
# classifier = MultinomiaNB()

classifier.fit(x_train, y_train)
print("훈련 세트 점수: {:.2f}".format(classifier.score(x_train,y_train)))
print("테스트 세트 점수: {:.2f}".format(classifier.score(x_test,y_test)))
visualize_classifier(classifier,x_test,y_test) #가시화 

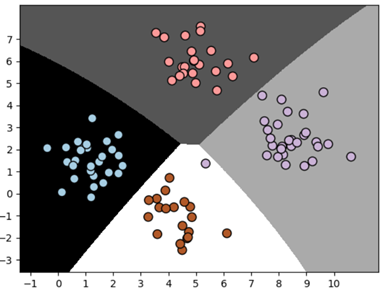
훈련 세트 점수: 1.00
테스트 세트 점수: 0.99