※ Deep Learning From Scratch (밑바닥부터 시작하는 딥러닝)에 대한 정리 자료입니다.
퍼셉트론
뉴런을 모방한 모델, 다수의 정보를 입력으로 받아 Reasonable하면 1, 그렇지 않으면 0을 출력하는 구조
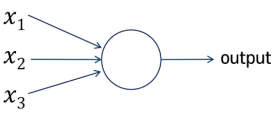
x: 입력, w: 가중치, theta: reasonable한 기준 (임계치)
(가중치가 곱해진 입력)의 합이 theta 이상이면 resonable한 정보라고 판단해서 1
(가중치가 곱해진 입력)의 합이 theta 미만이면 의미없는 정보라고 판단해서 0
[ (가중치가 곱해진 입력)의 합 예시: x1w1+x2w2+x3w3 ]
Function for AND Classifier
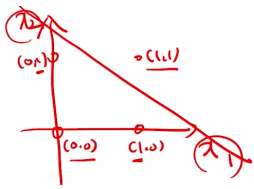
직선의 식: x1+x2-1.5=0 -> w1=1, w2=1, theta=1.5
ex) (x1,x2)=(1,1) -> x1w1+x2w2=2 >1.5이므로 1이 출력됨,
(x1,x2)=(1,0)->x1w1+x2w2=1<1.5이므로 0이 출력됨
theta 대신 b(bias)를 모델 식에 추가해도 된다. 이 때 b는 -theta이다.
ex) x1w1+x2w2가 theta이상이면 1, 아니면 0 (=) x1w1+x2w2+b가 0이상이면 1, 아니면 0
def AND(x1,x2):
w1,w2,theta=1,1,1.5
tmp=w1*x1+w2*x2
if tmp >= theta:
return 1
else:
return 0
(일반적인 코드)
def AND(x1,x2):
x=np.array([x1,x2])
w=np.array([[1],
[1]])
b=-1.5
tmp=np.dot(x,w)+b
if tmp >=0:
return 1
else:
return 0
(Numpy와 bias를 이용한 코드)
퍼셉트론의 수식적 표현
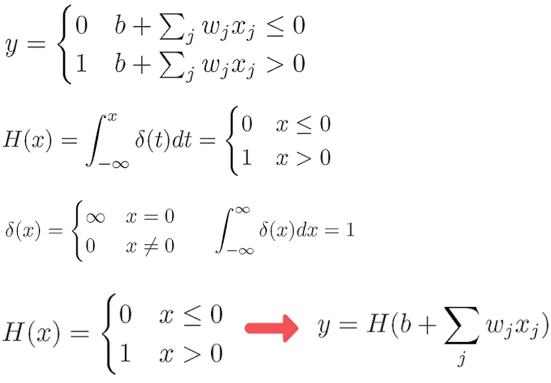
H(x)는 Heaviside Function 혹은 Step Function이라고 불린다.
OR 분류기와 XOR 분류기 시각화
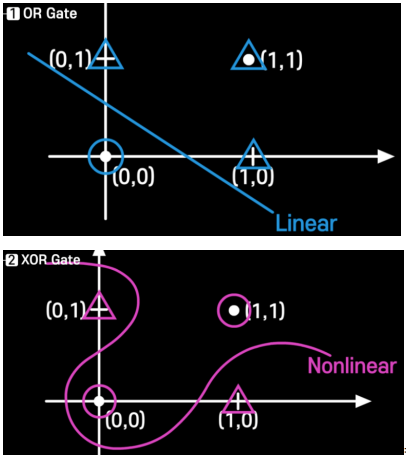
Limitation on Perceptron
하나의 퍼셉트론 모델(x1w1+x2w2+b)로는 XOR 분류를 할 수가 없다.
하나의 퍼셉트론 모델은 선형 모델이므로, 비선형 모델인 XOR 분류기를 만들 수가 없기 때문이다.
-> 하나의 퍼셉트론으로 할 수가 없다면 여러 개의 퍼셉트론으로 해결하자!
(실제로 선형 모델인 AND, NAND, OR 게이트를 결합해서 XOR 게이트를 만들 수 있다)
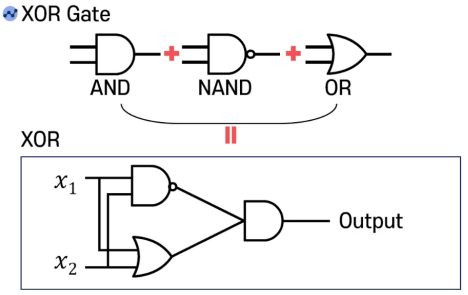
즉 Combination of Single Perceptron으로 비선형성 문제를 해결할 수 있다.
(비선형성 문제를 해결한다는 것이지 비선형 모양으로 변환된다는 것이 아니다)
Heaviside Function의 문제점
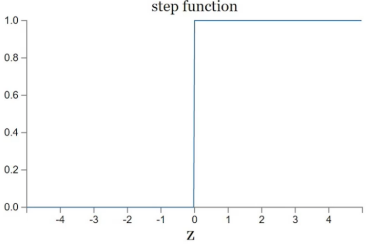
w(weight)나 b(bias)가 조금이라도 변하면 output이 급격하게 변할 수 있다.
ex) z가 -0.01에서 0.01이 되면 output이 0에서 1이 됨
이는 실제 의사 결정과는 괴리감이 있다. 정보가 조금 변했다고 결정이 확 변하는 경우는 드물기 때문이다.
-> 불연속점 근처를 smoothing out하게 만들자. 즉 연속이고 미분 가능하게 만들자!
-> Smoothing out된 H(x) 함수는 Activation Function이라고 부른다.
Well Known Activation Function
1. Sigmoid Function
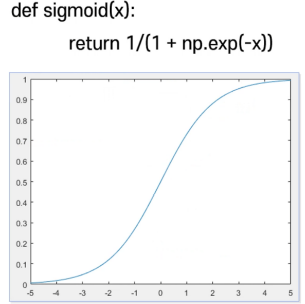
2. Arctan Function
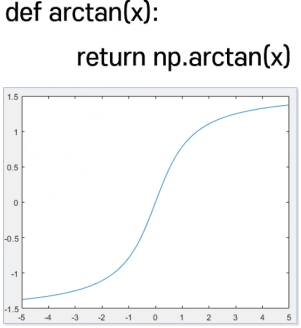
3. ReLU (Rectified Linear Unit) Function <Special Case>
: 0인 부분에서 미분이 불가능하지만 ReLU 함수가 좋은 결과를 줌
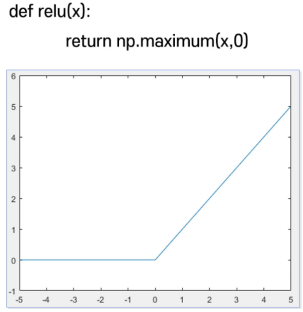
x=np.linspace(-5,5,101) ysim=sigmoid(x) plt.plot(x,ysim)
(시각화 코드)
Matrix Multiplication in Neural Network
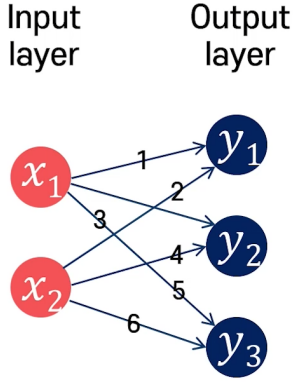
(x1+2*x2)=y1, (3*x1+4*x2)=y2, (5*x1+6*x2)=y3는 다음과 같이 행렬 곱으로 표현이 가능하다.
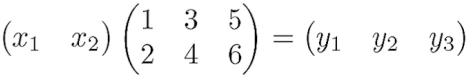
X=np.array([3,5])
W=np.array([[1,3,5],
[2,4,6]])
Y=np.dot(X,W)
Tip) 각 layer의 노드 수가 n이면, 행렬로 (1xn)으로 표현한다.
이전 layer의 노드 수가 i이고 다음 layer의 노드 수가 j이면, 사이에 있는 W(weights)는 (ixj)로 표현한다.
ex) 첫 번째 layer 노드 수: 2, 두 번째 layer 노드 수: 3 ->
첫 번째 layer: [x1,x2] (1×2), 두 번째 layer: [y1,y2,y3] (1×3), 사이의 W: [[1,3,5],[2,4,6]] (2×3)
Regression과 Classification
Regression: 주어진 데이터의 관계를 찾아내는 것
ex) y=f(xw+b)일 때 x는 자식의 키, y는 부모의 키 -> 자식 키를 이용해서 부모 키를 알 수 있음
-> output layer에 Identity Function을 이용함: f: I(a)=a
Classification: 데이터를 분류하는 것
ex) y1=f(x1w11+x2w12+b1), y2=f(x1w21+x2w22+b2)일 때 x1, x2는 꽃잎의 너비, 꽃잎의 길이고
y1은 무궁화일 확률, y2는 장미일 확률임 -> 확률이 높은 꽃으로 분류
-> output layer에 SoftMax Function을 이용함: f: Softmax(a)=e^ai/Sigma(i=1,…n) e^ai
Softmax Function
Ouput layer의 결과를 확률로 표시하기 위한 함수
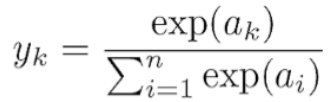
– a는 output layer node의 결과에 해당됨, 위 예시는 output layer node가 n개 있음
– 지수 함수(exp)를 이용하는 이유는 분자를 양수 값으로 가지기 위함 (확률이 음수면 안 되기 때문)
– yi부터 yn까지의 합은 1이 됨 (확률의 합은 1)
def softmax(a):
# a=[1,2,3]
exp_a=np.exp(a) # [e1,e2,e3]
sum_exp_a=np.sum(exp_a) # e1+e2+e3
y=exp_a/sum_exp_a # [e1/e1+e2+e3, e2/e1+e2+e3, e3/e1+e2+e3]
return y
-> 이렇게 구현하면 a원소의 값이 1000이면 e^1000이므로 오버플로우가 발생
(해결 방법)
1. Softmax의 분모와 분자에 같은 C를 곱함
2. C를 e^(log_e_C)로 변경함
3. e^a * e^(log_e_C)는 e^(a+log_e_C)와 같으므로 아래와 같이 식을 변경함
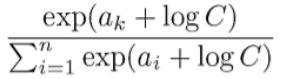
4. logC를 C’으로 표현함
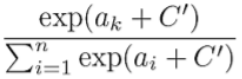
참고로 C’은 -max(a)를 자주 사용한다!
# 일반적인 Softmax a=np.array([1010,1000,990]) np.exp(a)/np.sum(np.exp(a)) # 개선한 Softmax a=np.array([1010,1000,990]) c=np.max(a) np.exp(a-c)/np.sum(np.exp(a-c))
Multi Layer Perceptron for Regression Code
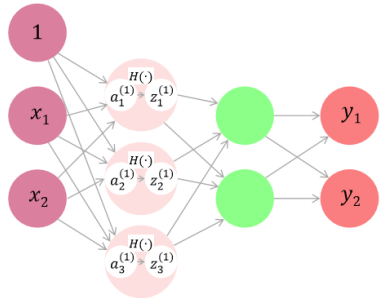
import numpy as np
def sigmoid(x):
return 1/(1+np.exp(-x))
def identity_function(x):
return x
def init_network():
network={}
# W1: 2X3, b1:1x3
network['W1']=np.array([[0.1,0.3,0.5],
[0.2,0.4,0.6]])
network['b1']=np.array([0.1,0.2,0.3])
# W2: 3X2, b2: 1x2
network['W2']=np.array([[0.1,0.4],
[0.2,0.5],
[0.3,0.6]])
network['b2']=np.array([0.1,0.2])
# W3: 2x2, b3: 1x2
network['W3']=np.array([[0.1,0.3],
[0.2,0.4]])
network['b3']=np.array([0.1,0.2])
return network
def forward(network,x):
W1,W2,W3=network['W1'],network['W2'],network['W3']
b1,b2,b3=network['b1'],network['b2'],network['b3']
a1=np.dot(x,W1)+b1
z1=sigmoid(a1)
a2=np.dot(z1,W2)+b2
z2=sigmoid(a2)
a3=np.dot(z2,W3)+b3
y=identity_function(a3)
return y
network=init_network()
x=np.array([1.0,0.5])
y=forward(network,x)
print(y)
Loss Function
모델을 평가하기 위한 함수 (값이 낮을수록 올바르게 예측)
아래 두 Loss는 배치 사이즈는 고려하지 않음 (배치 사이즈가 1인 경우)
1. MSE (Mean Squared Error)
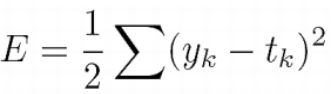
output layer node 수가 n개이므로, 1/n을 곱하는 게 일반적이지만,
미분을 편하게 하기 위해서 1/2을 곱하기도 함
2. CE (Cross Entropy)
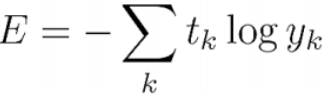
def cross_entropy_error(y,t):
delta=1e-7
return -np.sum(t*np.log(y+delta))
delta를 더해서 0이 나오는 것을 방지함 (log함수에 0이 입력되면 안 되기 때문)
[ MSE와 CE의 비교]
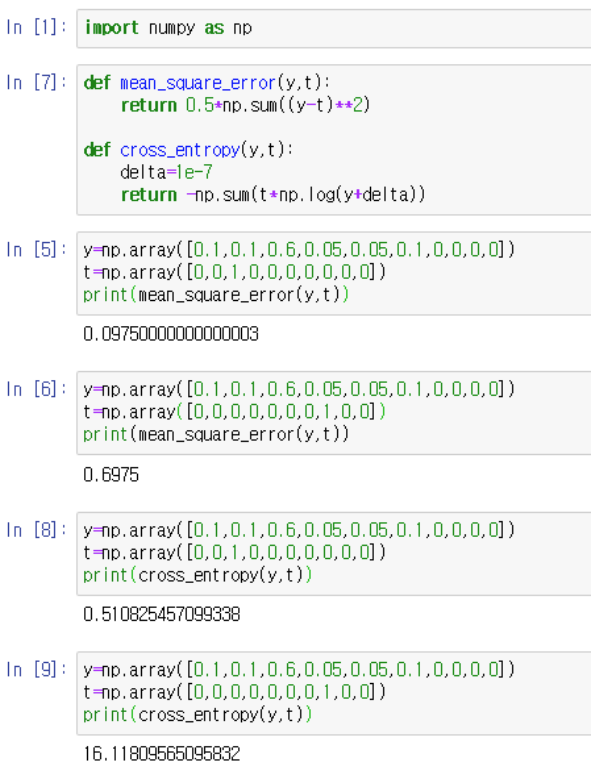
ln [5], [6]은 각각 예측이 올바른 경우와 틀린 경우에 계산한 MSE이다.
ln [8]. [9]는 각각 예측이 올바른 경우와 틀린 경우에 계산한 CE이다.
-> CE가 Error에 더 민감한 것을 확인할 수 있다. 또한 미분 값은 더 심하게 차이가 난다. 미분 값이 곱해져서 가중치를 변경하는데 사용되므로, 분류 문제에서는 CE를 사용하는 것이 더 유리하다.
Gradient and Loss
Gradient Vector
각 축 방향으로 편미분한 값을 원소로 가지는 벡터
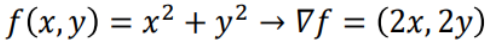
Gradient Descent
loss를 최소화하는 방법으로, Gradient의 절댓값이 감소하는 방향으로 loss의 입력에 해당하는 x나 y를 변화시키는 것이다. Gradient의 절댓값이 감소하는 방향은 -Gradient 방향으로 간다는 말과 같은데, -Gradient 방향으로 간다는 것은 함수 값을 가장 빨리 감소시키겠다는 의미이다. (수학적으로 증명됨)
따라서 loss가 줄어드는 방향으로 x와 y가 변하게 된다.
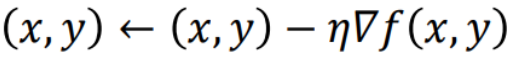
n은 learning rate 혹은 step size로 불리며, x와 y를 업데이트할 때 가중치 역할을 한다.
n이 크면 x,y가 급격하게 변하므로 loss가 크게 줄어든다.
n이 작으면 x,y가 조금만 변하므로 loss가 작게 줄어든다.
[예시]
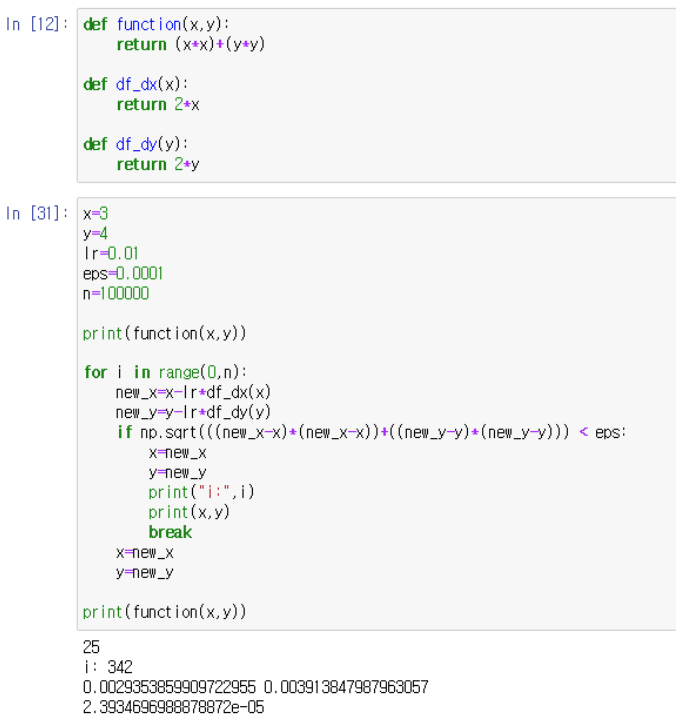
x와 y를 342번 업데이트했을 때 loss를 최소치로 근사화할 수 있다.
조건문 식의 의미: loss의 입력에 해당하는 x와 y가 더이상 변화하지 않을 때까지 진행한다.
즉 x와 새로운 x의 차이, y와 새로운 y의 차이가 거의 없을 때까지 업데이트한다는 의미이다.
이것은 (x,y)와 (new_x,new_y)의 거리가 최대한 작을 때까지(eps보다 작을 때까지)한다는 의미와 같다.
왜 차이가 점점 작아지는가?: Gradient의 절댓값이 감소하는 방향으로 값을 변화시키니까 나중에는 Gradient의 절댓값이 0에 가까워지므로 x,y값은 거의 변화되지 않는다.
Numerical Differentiation
Differentiation: 변화율
아래는 순간변화율로, 미분에 해당한다.
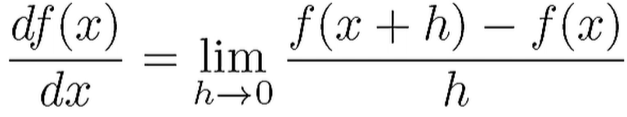
아래와 같이 미분을 근사화해서 계산할 수도 있다. 이것을 Numerical Differentiation의 1st order라고 한다.
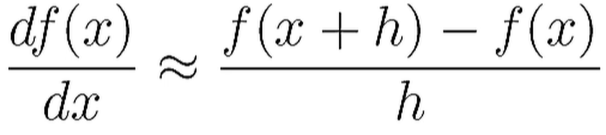
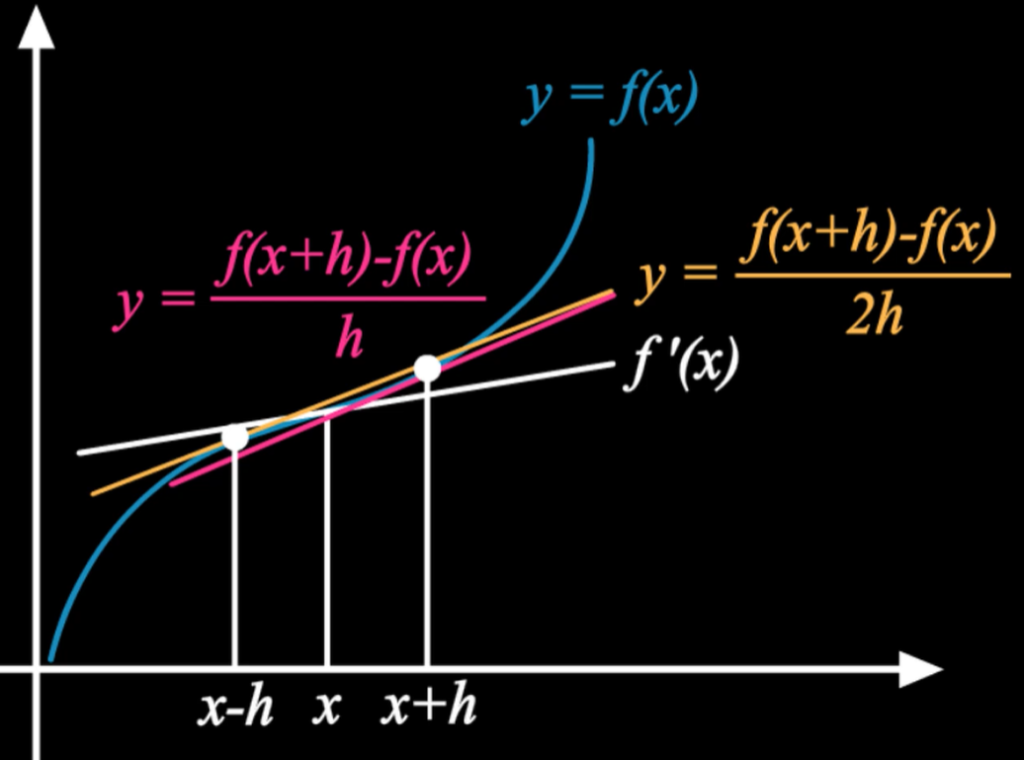
하지만 1st order를 사용하면 정확하지 않으므로, 아래와 같이 2nd order를 사용하는 것이 더 정확하다.
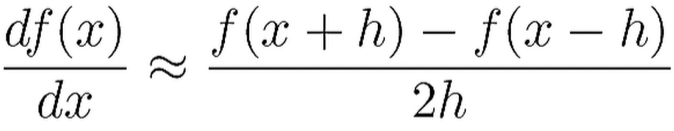
실제로 아래처럼 그림을 그려보면 2nd order가 f'(x)의 계형과 더 비슷하다.
Numerical Differentiation 코드
def numerical_diff(f,x):
h=1e-4 # 0.0001
return (f(x+h)-f(x-h))/(2*h)
Numerical Differentiation 코드 (편미분)
def numerical_gradient(f,x):
h=1e-4
grad=np.zeros_like(x)
for idx in range(x.size):
tmp_val=x[idx] # 값 저장
# f(x+h) 계산
x[idx]=tmp_val+h
fxh1=f(x)
# f(x-h) 계산
x[idx]=tmp_val-h
fxh2=f(x)
grad[idx]=(fxh1-fxh2)/(2*h)
x[idx]=tmp_val # 값 복원
return grad
# 예시 (f=x0^2+x1^2)
def function(x):
return x[0]**2+x[1]**2
numerical_gradient(fuction,np.array([3.0, 4.0]))
# 결과
# ---> array([6., 8.])
활용
일반적인 미분 식은 lim (h->0) f(x+h)-f(x)/h이다. 이를 코드를 통해 구현할 때는 h를 최대한 작은 값으로 주기 위해 1e-50 따위를 이용한다. 하지만 이렇게 계산하는 경우, Round Error가 발생한다. Round Error는 작은 값(가령 소수점 8자리 이하)이 생략되어 최종 계산 결과에 오차가 생기는 문제이다. 따라서 일반적인 미분 대신 수치 미분(Numerical Differentiation)을 사용해서 근사화해서 계산하는 것이 최선이다. 이 때, 1st order(전진 차분)보다는 2nd order(중앙 차분)이 더욱 정확하다.
Numerical Differentiation Problem


f(x+h)는 사실 f(x0+h)에 해당한다.
Talylor series의 x자리에 (x0+h)를 대입하고, 결과 식에서 x0를 x로 변환한 뒤 표현한 것이다.
f(x-h)도 마찬가지이다.
