PCA 차원 축소는 데이터 시각화에서 자주 사용되는 기법입니다.
고차원에서 데이터를 표현한 것보다 저차원에서 데이터를 표현한 것이 더 이해하기 쉽습니다!
예를 들어 5차원 데이터를 표현하려고 하는데 이것을 5차원 공간에 표현하는 것보다는
1차원 공간에 표현하는 것이 훨씬 이해하기 쉽습니다!
어떤 방식으로 차원 축소가 일어나는지 한 번 2차원 데이터로 예시를 보이겠습니다!

2차원 공간 상에 있는 점들을 어떻게 1차원으로 줄일 수 있을까요?
가장 기본적으로 생각할 수 있는 방법은 하나의 축에 점을 몰아 넣는 것입니다!
x1축 혹은 x2축을 이용하는 방법입니다!

그러나 이렇게 축소하니까 점들이 겹치게 되는 현상이 발생합니다!
차원 축소가 되면서 겹치는 점들이 생겼다는 것은 정보의 유실이 발생했다는 의미입니다.
결국 정보의 유실을 최소화하면서 1차원으로 축소할 방법이 필요합니다!

바로 분산을 최대화하는 직선을 이용하는 것입니다!
즉 선을 그을 때 점들이 가장 잘 퍼져있는 정도를 계산하면서 최적의 선을 찾는 방법입니다!
이렇게 하면, 점들이 퍼져 있는 정도를 지켜줌으로써 점들이 서로 겹치지 않고 하나의 공간에 모이게 됩니다!
이 방법을 수학적 알고리즘으로 제시한 것이 PCA입니다!

PCA는 고유값(Eigen Value)와 고유벡터(Eigen Vector) 개념을 이용합니다!
간략하게 말하면, 고유값은 데이터를 대표하는 값, 고유벡터는 고유값에 대응되는 벡터입니다!
고유값과 고유벡터는 데이터의 차원만큼 개수가 주어집니다!
본 예시는 2차원이니 2개의 고유값과 고유벡터(PC1, PC2)가 주어집니다!
따라서 큰 고유값에 대응되는 고유벡터(PC1)와 작은 고유값에 대응되는 고유벡터(PC2)가 존재합니다.
여기서 PC1이 바로 분산을 최대화하는 축에 해당이 됩니다!
이번에는 5차원 데이터로 예시를 보이겠습니다!

10명의 사람에 대하여 (calory~excercise)에 대한 특징과 body_shape라는 라벨이 주어져 있습니다!
일반적으로 5개의 특징을 시각화하려면 5차원 공간이 필요합니다!
그러나 우리는 1차원 공간으로 축소해서 표현하겠습니다!
1. 데이터와 라벨 분리
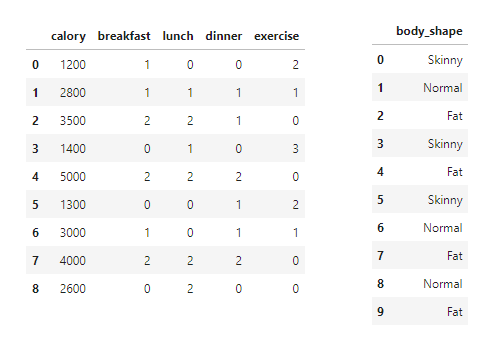
먼저 ‘특징이 담긴 데이터’와 ‘라벨’을 분리합니다!
차원 축소에 라벨은 무관하기 때문입니다.
2. 스케일링
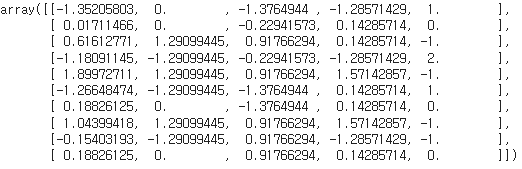
다음은 스케일링을 진행합니다.
스케일링은 데이터를 -1과 1사이로 표현하는 방법으로, 데이터에 평균을 빼고 표준편차로 나누는 방법을 사용합니다. 스케일링을 하면 데이터를 한쪽 방향(ex. calory)으로 치우치지 않고 확인할 수 있습니다.
3. 공분산 행렬 계산

10행 5열이었던 행렬을 5행 10열로 Transpose합니다.
이후 공분산 행렬(Covariace Matrix, Cx)을 계산합니다.
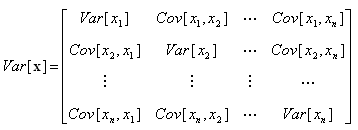
공분산(Covariance)은 두 확률변수의 관계(흩어지거나 밀집되는 정도)를 나타내는 값이고,
공분산 행렬(Covariance Matrix, Cx)은 공분산 값들을 저장하는 행렬입니다.
Cx의 각 원소는 Cov[xi,xj]에 해당이 되는데, 여기서 x는 확률변수를 의미하고 데이터의 특징과 매칭됩니다.
즉 x1~x5는 (calory에 대한 확률변수~excercise에 대한 확률변수)라고 생각하면 됩니다.
ex) Var[x1] = calory와 calory의 관계 (=) calory의 분산,
Cov[x1,x2] = calory와 breakfast의 관계 (=) calory와 breakfast의 공분산
이러한 공분산 행렬(Cx)은 고유값과 고유벡터를 구하는 데 사용이 됩니다!
4. 고유값과 고유벡터 계산


공분산 행렬을 이용하여 고유값과 고유벡터를 계산합니다.
고유값과 고유벡터는 데이터의 차원만큼 개수가 주어지므로
5개의 고유값과 고유벡터가 존재합니다.
여기서 가장 큰 고유값은 [4.0657343]으로, 전체 고유값에서 73%의 비율을 지닙니다!
이것은 73%의 데이터를 표현할 수 있다는 의미가 됩니다!
5. 데이터 시각화

가장 큰 고유값에 대응되는 고유벡터(PC1)로 데이터를 정사영(Projection)한 후 시각화를 한 모습입니다.
5차원 상에 존재해야 될 점들이 1차원 상에 표현되었습니다!
이후 라벨을 기준으로 색칠하였을 때, 비슷한 데이터끼리 잘 분포되는 것을 확인할 수 있습니다!
본 포스팅은 허민석님의 ‘PCA 강좌’ 영상을 정리한 글입니다.
원본 영상과 GitHub는 아래 링크와 같습니다!
1. [머신러닝] PCA 차원 축소 알고리즘 및 파이썬 구현 (주성분 분석)
: https://youtu.be/DUJ2vwjRQag
2. PCA.ipynb
: https://github.com/minsuk-heo/python_tutorial/blob/master/data_science/pca/PCA.ipynb
