이분 그래프 (Bipartite Graph)
- 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로
인접하지 않도록 분할할 수 있는 그래프 - 인접한 정점끼리 서로 다른 색으로 칠해서 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프

이분 그래프 판별하기
DFS를 이용해서 두 가지 색으로 정점 채색을 한다. 이후 모든 정점들을 순회하면서 인접한 정점과의 색이 같은지 확인한다. 만약 색이 같은 경우가 나오면 이분그래프가 아니다.
정점 채색
// DFS for Coloring
int visited[MAX_VERTICES];
void DFS(GraphType* g, int v) {
if (!visited[v])
visited[v] = RED;
if(visited[v] == RED)
printf("정점%d(RED) -> ", v+1);
else
printf("정점%d(BLUE) -> ", v + 1);
for (GraphNode* w = g->adj_list[v]; w; w = w->link) {
if (!visited[w->vertex]) {
if (visited[v] == RED)
visited[w->vertex] = BLUE;
else if (visited[v] == BLUE)
visited[w->vertex] = RED;
DFS(g, w->vertex);
}
}
}
DFS (깊이 우선 탐색): 먼저 정점 v를 방문한 다음, v에 인접한 정점 중에 아직 방문하지 않은 정점 w를 찾아서 w에 대한 DFS를 재귀적으로 수행한다. [ 시간복잡도: O(n+m), n은 정점의 개수, m은 에지의 개수 ]
DFS를 이용해서 정점의 색을 칠해준다. (RED or BLUE)
정점을 방문하지 않았으면 RED로 색칠한다.
현재 방문하고 있는 정점과 인접해있는 정점의 색을 현재 색과 다른 색으로 칠해준다.
(인접해있는 정점 중 아직 방문하지 않은 정점의 색을 다른 색으로 칠해줌)
이분 그래프 체크
bool Bipartite(GraphType* g) {
for (int i = 0; i < g->n; i++) {
GraphNode* p = g->adj_list[i];
int curr = i;
while (p != NULL) {
int next = p->vertex;
// check bipartite
if (visited[curr] == visited[next]) {
printf("[ERROR] %d %d\n", curr + 1, next + 1);
return false;
}
else
printf("[SUCCESS] %d %d\n", curr + 1, next + 1);
// update p
p = p->link;
}
}
return true;
}
연결되어 있는 모든 정점들을 검사한다.
만일 색이 같다면 그 즉시 false를 반환하고 (이분 그래프가 아님)
모든 정점을 검사해도 색이 같은 경우가 없으면 true를 반환한다. (이분그래프)
전체 코드 (C)
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#pragma warning(disable:4996)
#define MAX_VERTICES 100000
#define RED 1
#define BLUE 2
typedef struct GraphNode {
int vertex;
struct GraphNode* link;
}GraphNode;
typedef struct GraphType {
int n; // 정점의 개수
GraphNode* adj_list[MAX_VERTICES];
}GraphType;
// 그래프 초기화
void init(GraphType* g) {
int v;
g->n = 0;
for (v = 0; v < MAX_VERTICES; v++)
g->adj_list[v] = NULL;
}
// 정점 삽입 연산
void insert_vertex(GraphType* g, int v) {
if ((g->n) + 1 > MAX_VERTICES) {
fprintf(stderr, "그래프: 정점의 개수 초과");
return;
}
g->n++;
}
// 간선 삽입 연산, v를 u의 인접 리스트에 삽입한다.
void insert_edge(GraphType* g, int u, int v) {
GraphNode* node;
if (u >= g->n || v >= g->n) {
fprintf(stderr, "그래프: 정점 번호 오류");
return;
}
if (g->adj_list[u] == NULL) { // insert_first
node = (GraphNode*)malloc(sizeof(GraphNode));
node->vertex = v;
node->link = g->adj_list[u];
g->adj_list[u] = node;
}
else { //insert_last
node = g->adj_list[u];
while (node->link != NULL)
node = node->link;
node->link = (GraphNode*)malloc(sizeof(GraphNode));
node->link->vertex = v;
node->link->link = NULL;
}
}
// DFS for Coloring
int visited[MAX_VERTICES];
void DFS(GraphType* g, int v) {
if (!visited[v])
visited[v] = RED;
if(visited[v] == RED)
printf("정점%d(RED) -> ", v+1);
else
printf("정점%d(BLUE) -> ", v + 1);
for (GraphNode* w = g->adj_list[v]; w; w = w->link) {
if (!visited[w->vertex]) {
if (visited[v] == RED)
visited[w->vertex] = BLUE;
else if (visited[v] == BLUE)
visited[w->vertex] = RED;
DFS(g, w->vertex);
}
}
}
// 이분 그래프 체크
bool Bipartite(GraphType* g) {
for (int i = 0; i < g->n; i++) {
GraphNode* p = g->adj_list[i];
int curr = i;
while (p != NULL) {
int next = p->vertex;
// check bipartite
if (visited[curr] == visited[next]) {
printf("[ERROR] %d %d\n", curr + 1, next + 1);
return false;
}
else
printf("[SUCCESS] %d %d\n", curr + 1, next + 1);
// update p
p = p->link;
}
}
return true;
}
// 그래프 출력
void print_adj_list(GraphType* g) {
for (int i = 0; i < g->n; i++) {
GraphNode* p = g->adj_list[i];
printf("정정 %d의 인접 리스트", i+1);
while (p != NULL) {
printf("-> %d", p->vertex+1);
p = p->link;
}
printf("\n");
}
}
int main() {
GraphType* g;
g = (GraphType*)malloc(sizeof(GraphType));
init(g);
// 정점, 에지 개수 입력
int n, m;
scanf("%d %d", &n, &m);
// 정점 삽입
for (int i = 0; i < n; i++)
insert_vertex(g, i);
// 에지 삽입
for (int i = 0; i < m; i++) {
int u, v;
scanf("%d %d", &u, &v);
// 정점이 0부터 시작하므로 1씩 제거
u = u - 1;
v = v - 1;
insert_edge(g, u, v); // vertex(u) -> vertex(v)
insert_edge(g, v, u); // vertex(v) -> vertex(u)
}
print_adj_list(g);
printf("\n");
// DFS로 색칠
DFS(g, 0);
printf("\n");
// 이분그래프 판별
bool output = Bipartite(g);
if (output)
printf("%d", 1);
else
printf("%d", -1);
free(g);
return 0;
}
인접 리스트를 이용한 DFS 구현 + 이분 그래프 판별
[ 시간복잡도: O(n+m), n은 정점의 개수, m은 에지의 개수 ]
테스트 결과 예시

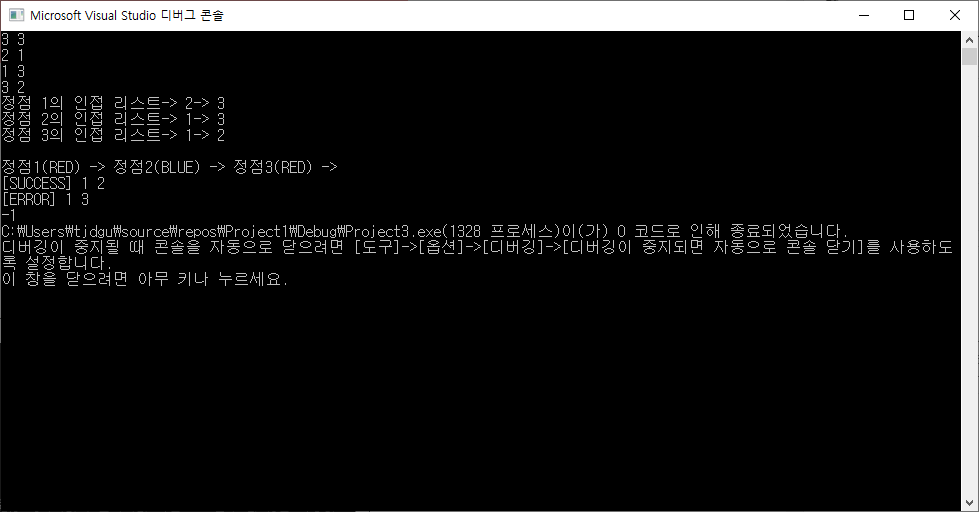
입력: 3 3 (정점 개수, 에지 개수) 2 1 1 3 3 2 (에지)
출력: -1 (이분 그래프가 아님)
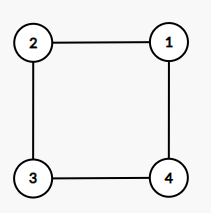
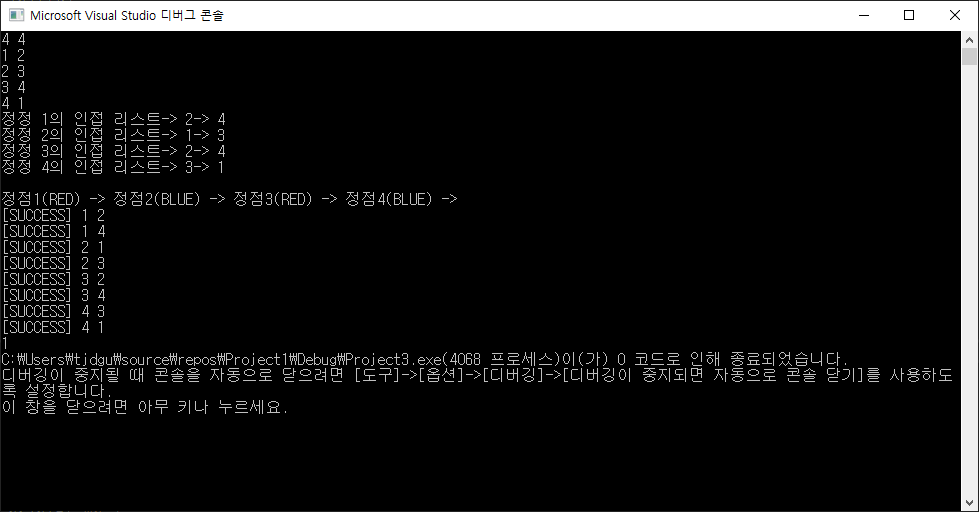
입력: 4 4 (정점 개수, 에지 개수) 1 2 2 3 3 4 4 1 (에지)
출력: 1 (이분 그래프)
