알고리즘 – quickSelect와 MoM

By MasterAlgorithm, CSE

quickSelect는 리스트에서 k번째로 작은 원소를 반환하는 로직(k-selection) 중 하나이다.
k-selection 중에서는 가장 빠르다고 알려져있다.

다음은 quickSelect 알고리즘이다. (quickSort와 유사함)

1. p(pivot)를 고른다. (배열의 첫 번째 원소, 마지막 원소, 랜덤 원소 등)
2. L={p보다 작은 값}, R={p보다 큰 값}, M={p와 같은 값} 집합을 각각 만든다. (n-1번 비교)
3-1. |L|이 k보다 크거나 같으면 k번째로 작은 수는 L 집합에 위치하므로 L에서 k번째로 작은 값을 찾는다.
(재귀적으로 찾음)
3-2. |L|+|M|이 k보다 작으면 k번째 작은 수는 R 집합에 위치하므로 B에서 k-(|L|+|M|)번째로 작은 값을 찾는다.
(재귀적으로 찾음)
3-3. k번째 작은 수는 M 집합에 위치하므로 p를 리턴한다.

quickSelect의 C++ Code는 아래와 같다.

int quickSelect(vector<int> arr, int k) {
	// 피벗 생성 (1번 과정) 
	int p = arr[0];

	// Partition (2번 과정)
	vector<int> L;
	vector<int> R;
	vector<int> M;
	for (int& x : arr) {
		if (p > x)
			L.push_back(x);
		else if (p < x)
			R.push_back(x);
		else
			M.push_back(x);
	}

	// K번째로 작은 원소 리턴 (3번 과정) 

	// (1) |L|이 k보다 크거나 같으면 k번째로 작은 수는 L 배열에 위치하므로 L에서 k번째로 작은 값을 찾는다.
	if (L.size() >= k)
		return quickSelect(L, k);
	// (2) |L|+|M|이 k보다 작으면 k번째로 작은 수는 R 집합에 위치하므로 R에서 k-(|L|+|M|)번째로 작은 값을 찾는다. 
	else if (L.size() + M.size() < k)
		return quickSelect(R, k - (L.size() + M.size()));
	// (3) k번째 작은 수는 M 집합에 위치하므로 p를 리턴
	else
		return p;
}

quickSelect의 Worst Case를 조사해보겠다.

n이 리스트의 크기일 때,
pivot이 최댓값 or 최솟값으로 선정되면 L이 n-1개의 원소를 지니거나 R이 n-1개의 원소를 지닌다.
L에서 찾기로 했는데 pivot이 다시 최댓값 or 최솟값으로 선정되면 다시 L가 n-2개의 원소를 지니거나 R이 n-2개의 원소를 지닌다.
이렇게 pivot이 최댓값or최솟값이 되는 경우가 반복되는 경우가 최악의 경우이다.

n개에서 찾는 것을 n-1개에서 찾음 ->
n-1개에서 찾는 것을 n-2개에서 찾음 ->
n-2개에서 찾는 것을 n-3개에서 찾음
을 반복하니 T(n)= T(n-1)+n이 된다.
(여기서 ‘+n’은 2번 과정에서 n-1번 비교하는 것)

T(n)=1+2+….+n으로 나타낼 수 있으므로
T(n)=n(n+1)/2이고 O(n2)이 된다.

하지만 O(n2)인 알고리즘은 n이 100,000만 되더라도 오랜 시간이 소요된다.

우리는 이 때, Median of Medians라고 하는 알고리즘을 사용하면 된다.
이 알고리즘을 사용하면 중앙값과 비슷한 값(MoM)을 빠른 시간안에 리턴할 수 있다.
이후 MoM을 pivot으로 사용하면 된다!

다음은 Median of Medians 알고리즘이다.

1. 전체 배열에서 5개의 원소를 가지는 그룹(sub array)을 만든다. (n/5개의 그룹 생성)

2. 각 그룹의 중앙값(median)을 찾는다.

3. 중앙값들 중 중앙값을 찾는다. (재귀적으로 찾음)
-> mom = MoM(medians)

Median of Medians의 C++ Code는 아래와 같다.

// 5개 이하의 원소 중 중앙값 찾기 
int medianOfFive(vector<int> arr) {
	sort(arr.begin(), arr.end());
	return arr[arr.size() / 2];
}

// Median of Medians 알고리즘
int MoM(vector<int> arr) {
	// 배열의 크기가 5 이하일 경우에는 sort해서 반환
	if (arr.size() <= 5) {
		return medianOfFive(arr);
	}

	// sub array를 만들 개수
	// ex) arr={1,2,3,4,5}->m=1, arr={1,2,3,4,5,6}->m=2, arr={1,2,3,4,5,6,7}->m=2
	int m = (arr.size() + 4) / 5;

	// medians를 모아놓을 배열
	vector<int> M;

	// subarray의 median을 M배열에 추가 (1~2번 과정)
	for (int i = 0; i < m; i++) {
		// 5개의 원소를 저장할 sub 배열 
		vector<int> sub;
		for (int j = 0; j < 5; j++)
			// arr 배열에 존재하는 원소에 대해서만 추가 
			if ((5 * i + j) < arr.size())
				sub.push_back(arr[5 * i + j]);
		M.push_back(medianOfFive(sub));
	}

	// MoM을 재귀 호출해서 찾아낸다 (3번 과정)
	int mom = MoM(M);
	return mom;
}

이번에는 MoM을 pivot으로 사용하면 왜 유리한지 알아보겠다!

우리는 quickSelect 알고리즘에서 배열의 크기가 n인 문제를 풀기 위해 배열의 크기가 |L|이거나 |R|인 문제를 풀어야 했다. 즉 T(n)을 풀기 위해 T(|L|) or T(|R|)을 풀어야 했다.

그런데 만약 MoM을 사용하면, |L|과 |R|은 항상 7n/10 이하가 된다!

구간별로 오름차순 정렬되었고(위->아래) medians들이 오름차순 정렬되었다고 가정하자(왼쪽->오른쪽).
그럼 mm은 정중앙에 위치하고 mm의 북서쪽(North-West) 원소들은 mm보다 작거나 같게 된다.
mm의 남동쪽(South-East) 원소들은 mm보다 크거나 같게 된다.

이 때 북서쪽(North-West)이나 남동쪽의 원소(South-East)는 (n/5×1/2)개의 그룹에서 각 그룹 당 절반 개의 원소에 해당하므로 (n/5×1/2)x3=3n/10이 된다.

그러나 북동쪽, 남서쪽 원소들도 고려해야 된다.
북동쪽, 남서쪽의 원소는 mm보다 클 수도 있고 작을 수도 있다.
즉 남동쪽(South-East)을 제외한 모든 원소가 mm보다 작아 mm보다 작은 원소 수는 7n/10이 될 수 있다.
반대로 북서쪽(North-West)을 제외한 모든 원소가 mm보다 커서 mm보다 큰 원소 수는 7n/10이 될 수 있다.

quickselect알고리즘은 pivot보다 작은 구간(L)이나 큰 구간(R)을 확인하는데, 해당 구간의 최대 원소 수는 7n/10이 된다는 의미이다.

따라서 |L|과 |R|은 항상 7n/10 이하가 된다!

다시 quickSelect의 Worst Case를 조사하겠다.
이번에는 MoM의 시간복잡도까지 고려해야 한다!

W(n) = n-원소 집합에서 quickSelect를 위한 최악의 경우 비교 횟수라고 하자.

  1. 5개의 원소에서 중앙값을 찾을 때는 6번 비교한다. 그런데 중앙값을 그룹마다 찾아야하니 총 n/5 x 6번을 비교한다.
  2. MoM을 재귀적으로 찾을 때 medians를 배열로 사용하니 W(n/5)번 비교한다.
  3. quickSelect의 Partition하는 과정에서 모든 원소를 비교하니 총 n번 비교한다.
  4. quickSelect를 재귀적으로 찾을 때 L집합이나 R집합을 사용하니 최악의 경우, W(7n/10)번 비교한다.

결국 W(n) = 11/5n + W(n/5) + W(7n/10)을 만족한다.

W(n)으로 시간복잡도를 구할 때는 재귀 트리(Recursion Tree)를 이용한다.

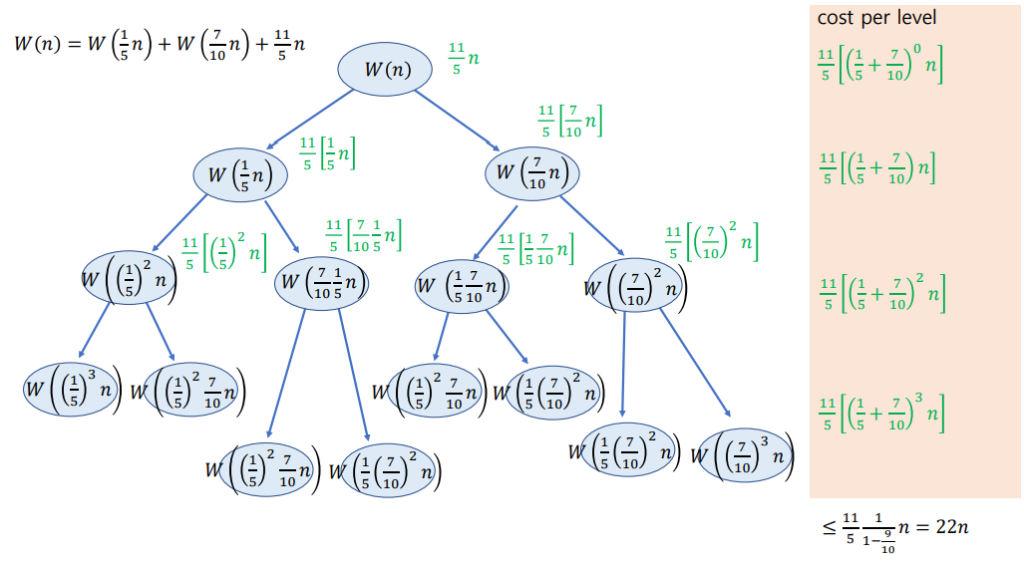
시간복잡도는 O(n)을 만족하지만
상수가 너무 크기 때문에 MoM이 효율적이라고 말할 수는 없다.
오히려 힙정렬이나 합병정렬을 하고 k번째 원소를 반환하는 것이 나은 수준이다.

하지만 MoM의 아이디어 자체는 다른 알고리즘에도 많은 영감을 주었다고 한다.

마지막으로 quickSelect with MoM의 C++ 예제이다.

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

// 5개 이하의 원소 중 중앙값 찾기 
int medianOfFive(vector<int> arr) {
	sort(arr.begin(), arr.end());
	return arr[arr.size() / 2];
}

// Median of Medians 알고리즘
int MoM(vector<int> arr) {
	// 배열의 크기가 5 이하일 경우에는 sort해서 반환
	if (arr.size() <= 5) {
		return medianOfFive(arr);
	}

	// sub array를 만들 개수
	// ex) arr={1,2,3,4,5}->m=1, arr={1,2,3,4,5,6}->m=2, arr={1,2,3,4,5,6,7}->m=2
	int m = (arr.size() + 4) / 5;

	// medians를 모아놓을 배열
	vector<int> M;

	// subarray의 median을 M배열에 추가
	for (int i = 0; i < m; i++) {
		// 5개의 원소를 저장할 sub 배열 
		vector<int> sub;
		for (int j = 0; j < 5; j++)
			// arr 배열에 존재하는 원소에 대해서만 추가 
			if ((5 * i + j) < arr.size())
				sub.push_back(arr[5 * i + j]);
		M.push_back(medianOfFive(sub));
	}

	// MoM을 재귀 호출해서 찾아낸다
	int mom = MoM(M);
	return mom;
}

int quickSelect(vector<int> arr, int k) {
	// 피벗 생성 
	int p = MoM(arr);

	// Partition
	vector<int> L;
	vector<int> R;
	vector<int> M;
	for (int& x : arr) {
		if (p > x)
			L.push_back(x);
		else if (p < x)
			R.push_back(x);
		else
			M.push_back(x);
	}

	// K번째로 작은 원소 리턴

	// (1) |L|이 k보다 크거나 같으면 k번째로 작은 수는 L 배열에 위치하므로 L에서 k번째로 작은 값을 찾는다.
	if (L.size() >= k)
		return quickSelect(L, k);
	// (2) |L|+|M|이 k보다 작으면 k번째로 작은 수는 R 집합에 위치하므로 R에서 k-(|L|+|M|)번째로 작은 값을 찾는다. 
	else if (L.size() + M.size() < k)
		return quickSelect(R, k - (L.size() + M.size()));
	// (3) k번째 작은 수는 M 집합에 위치하므로 p를 리턴
	else
		return p;
}

int main() {
	// 1~100000이 순서대로 저장된 배열 
	vector<int> data;
	data.reserve(100000);
	for (int i = 1; i <= 100000; i++) {
		data.push_back(i);
	}

	// k_selection 결과는 k가 나와야 한다.
	int k = 99999;
	cout << "k_selection : " << quickSelect(data, k) << endl;

	return 0;
}

data는 1~100,000이 순서대로 저장된 배열이다.
k=99,999로 선정했다.
pivot이 data[0]으로 선정되면 최악의 경우에 해당하니 1초 안에 해결할 수 없다.
pivot이 MoM으로 선정되면 최악의 경우에도 1초 안에 해결이 가능하다.

Leave a Reply

Your email address will not be published. Required fields are marked *