알고리즘의 증명 방법은 크게 귀류법과 귀납법이 존재한다.
귀류법은 정답이 아니라고 가정하고 모순에 의해 증명하는 방법이다.
지금부터 귀류법 증명에 대한 예시 3가지를 보이겠다.
1. √2는 유리수가 아니다.
√2는 유리수라고 가정해 보자. 유리수는 두 정수(a, b)의 나눗셈(a/b)으로 표현할 수 있는 숫자이다.
이 때 두 정수 (a, b)는 서로소(GCD=1)이다. 그러면 √2는 a/b이고 √2b=a로 표현할 수 있다.
a2=2b2이므로 a2이 짝수가 되고, a2이 짝수이므로 a도 짝수가 된다.
이제 a=2c로 표현할 수 있다.
그러면 2b2=4c2이고 b2=2c2이므로 b도 짝수가 된다.
a와 b가 짝수이므로 서로소가 아니게 되므로 유리수의 정의에 모순된다.
모순이 발생한 이유는 √2는 유리수라고 가정했기 때문이다.
따라서 √2는 유리수가 아니다.
2. 소수는 무한하다.
소수는 유한하다고 가정해 보자.
소수는 유한하니까 모든 소수에 대해 n개로 나타낼 수 있다. (p1, p2, p3, … , pn)
1과 pk(k=1~n)가 아닌 나머지 자연수는 모두 합성수가 되어야 한다.
(합성수: 1보다 큰 자연수 중에서 소수가 아닌 수)
합성수는 소수로 나눠진다는 특징이 있다.
그러나 [p1 x p2 x … x pn +1]이라는 합성수 N이 주어질 때, N은 어떤 pk(k=1~n)로도 나눠질 수 없다.
모순이 발생한 이유는 소수는 유한하다고 가정했기 때문이다.
따라서 소수는 무한하다.
3. 연결된 그래프의 정점v에서 DFS(v)를 실행하면 모든 정점을 방문한다.

연결된 그래프에서 DFS를 실행해도 모든 정점을 방문하지는 않는다고 가정해 보자.
가정에 의하면 DFS가 종료될 때, visited[v]=false인 v가 존재한다. (0 <= v <= vertex_size-1)
그러나 DFS가 첫 번째 호출이든 재귀 호출(인접한 정점 확인)이든 ‘visited[v]=true’라는 코드를 항상 실행하게 된다.
또한 연결된 그래프이므로 모든 정점에 대하여 DFS를 호출하는 구조이다.
결국 DFS가 종료되면 가능한 모든 v에 대하여 visited[v]=True가 된다.
이러한 모순이 발생한 이유는 가정이 틀렸기 때문이다.
따라서 연결된 그래프의 정점v에서 DFS(v)를 실행하면 모든 정점을 방문한다.
귀납법은 정답이라고 가정하고 모든 경우에 대해 증명하는 방법이다.
지금부터 귀납법 증명에 대한 예시 3가지를 보이겠다.
1. n>=1일 때 아래 수식이 성립한다.
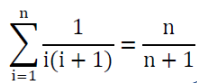
case1) n = 1 <답 비교>
정답이라고 가정한 값과 실제 정답을 확인한다.
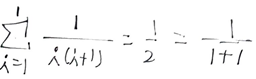
case2) n >=2 <정답이라고 가정해도 문제가 없는지 확인>
(i<=n-1에 대하여 정답이라고 가정한 값)과 (i=n일 때의 값)을 더했을 때,
(i<=n에 대하여 정답이라고 가정한 값)과 같은지 확인한다.

즉 식을 나눈 다음 가정을 적용해도 최종적으로 나온 sigma값은 차이가 없다.
모든 case에 대해 주어진 성질을 만족하므로 위 수식은 성립한다.
2. 트리에서 정점과 에지의 개수를 n, e라고 하면 e=n-1이다.
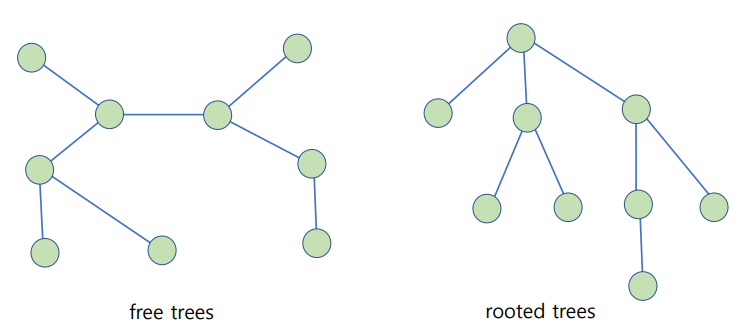
case 1) n<=9 <답 비교>
트리를 그려서 직접 에지의 개수를 세 본 결과 n-1이 나온다.
case 2) n > 9 <정답이라고 가정해도 문제가 없는지 확인>

서브 트리가 d개 있다고 가정하겠다.
각 서브 트리의 에지 개수를 e1,e2,…ed라고 하였을 때, e=n-1이라고 가정하면
e1=n1-1, e2=n2-1, e3=n3-1, … , ed=nd-1이 된다.
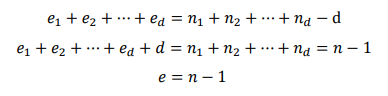
e1~ed를 모두 합치면 n1+n2+…+nd-d가 나온다.
e1~ed를 모두 합친 값은 e(트리 에지 개수)-d(서브 트리 개수)와 같고
n1~nd를 모두 합친 값은 n(트리 정점 개수)-1과 같으므로
e-d+d=n-1 (->) e=n-1이 성립한다.
즉 서브 트리에 대해 가정을 적용해도 최종적으로 나온 e값은 차이가 없다.
모든 case에 대해 주어진 성질을 만족하므로 위 수식은 성립한다.
3. 이진트리 T의 외부 경로 길이(external path length; epl)는 mlog2m 이상이다.
(epl: 루트~외부 노드까지의 거리 합, m=외부 노드의 개수, n=내부 노드의 개수, m=n+1)
epl(T) >= mlog2m이라고 가정하면,
Left 서브트리, Right 서브트리에 대해서
epl(TL) >= mLlog2mL, epl(TR) >= mRlog2mR 이 성립한다.
또한 epl(T) = epl(TL) + epl(TR) + mL + mR 과
m = mL + mR 이 성립하므로
epl(T) – m = epl(TL) + epl(TR) >= mLlog2mL + mRlog2mR 이 성립한다.
이 때, y=xlog2x 그래프는 아래와 같다.

여기서 주의 깊게 바라볼 부분은
(mLlog2mL + mRlog2mR)/2 >= f((mL + mR)/2)
이고 f((mL + mR)/2) = ((mL + mR)/2)log2((mL + mR)/2)이므로
(epl(T) – m) / 2 >= (mLlog2mL + mRlog2mR) / 2 >= ((mL + mR) / 2)log2((mL + mR) / 2)가 된다.
즉 epl(T) – m >= mlog2(m / 2)이 된다.
식은 다시 epl(T) – m >= m(log2m-1)로 정리되므로
epl(T) >= mlog2(m)을 만족한다.
즉 서브 트리에 대해 가정을 적용해도 최종적으로 나온 epl값은 차이가 없다.
알고리즘의 정확성을 나타내기 위해서는 수학적 귀납법이 주로 쓰이니 귀납법은 숙지해두는 편이 좋다.
