분할 정복은 문제를 a개의 더 작은 부분 문제로 나누고(divide), 각각을 재귀적으로 해결한 다음(conquer), a개의 부분 해를 합하여(merge) 전체 문제의 하나의 해로 만들어 내는 것이다.

분할 정복의 시간 복잡도는 마스터 정리를 통해 구할 수 있다.

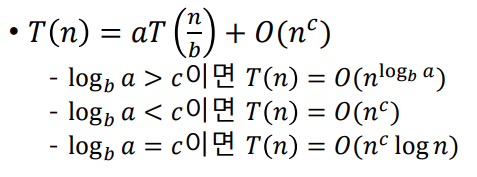
(약속) 모든 n은 (2^k-2 < n <= 2^k)를 만족함 -> 시간복잡도 계산할 때 n=2^k

분할 정복법의 시간 복잡도에서 a, T(n/b), O(n^c)는 각각 다음을 의미한다.

a: 분할하는 구간
T(n/b): 분할할 때 걸리는 시간
O(n^c): 합병할 때 걸리는 시간

예를 들어 [a=3, b=2, c=1]이라고 하면
[세 구간씩 분할, 분할할 때 T(n/2)시간, 합병할 때 n시간]이라는 의미이다.

참고로 T(n)은 합병 시간의 합으로 표현할 수 있다.
(시간=분할시간+합병시간이고, 분할시간은 분할시간+합병시간인데 이것을 반복하면 마지막 분할 시간이 0이 되므로 결국 합병시간의 합이 됨)

즉 재귀 트리 각 레벨의 합병 시간을 모두 더하면 T(n)이 나온다.

재귀 트리로 구한 시간 복잡도가 마스터 정리와 같은지 확인해보자.
(초록 글씨: 합병 시간)

1. log_ba > c인 경우 (a=3, b=2, c=1)

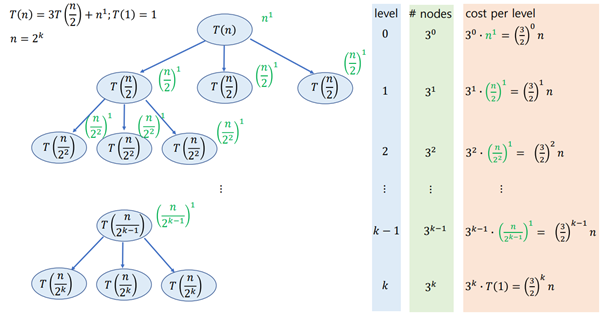
• 맨 마지막 노드인 T(n/2^k)=T(1)는 분할을 안 하고 자기 자신으로 합병 1(n/2^k)번 만 진행함

첫 번째 합병(높이:0)할 때는 n 시간 x 노드의 개수(3⁰)
두 번째 합병(높이:1)할 때는 n/2 시간 x 노드의 개수(3¹)
세 번째 합병(높이:2)할 때는 n/2² 시간 x 노드의 개수(3²)
…..
k번째 합병(높이:k-1)할 때는 n/2^k-1시간 x 노드의 개수(3^k-1)
k+1번째 합병(높이:k)할 때는 T(n/2^k)에 대한 문제 -> T(1)에 대한 문제 x 노드의 개수(3^k)

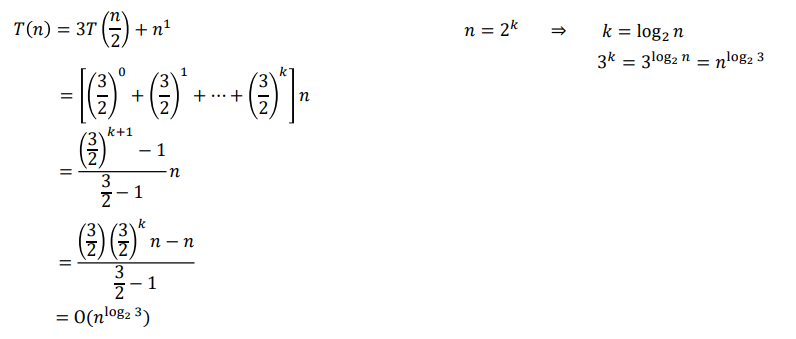
식을 정리해서 나온 3^k+1-2^k+1에서 3^k=n^log₂3이므로, 3n^log₂3-2n=O(n^log₂3)이 됨

2. log_ba < c인 경우 (a=3, b=2, c=2)

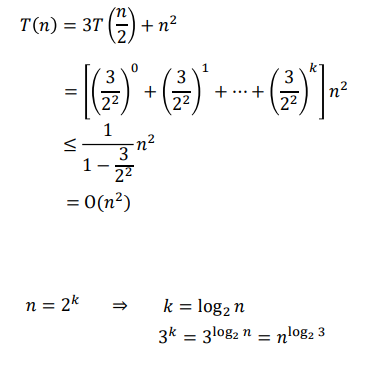
3. log_ba = c인 경우 (a=3, b=2, c=log₂3)