구간 그래프

구간을 정점, 구간이 겹치는 것을 엣지로 표현한 그래프

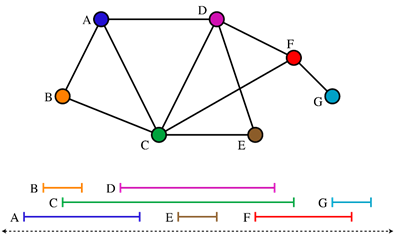
구간 그래프 관련 용어

• 독립 집합: 그래프에서 서로 인접하지 않은 정점들의 집합 (겹치지 않는 구간들 모음)
• 최대 독립 집합: 독립집합 중 최대 정점 개수를 지닌 원소들로 이루어진 집합
• 정점 채색: 인접하면 다른 색이 되도록 색칠, 인접하지 않으면 같은 색 (독립 집합으로 분할)
• 클릭: 그래프에서 서로 인접한 정점들의 집합 (겹치는 구간들 모음)
• 최대 클릭: 클릭 중 최대 정점 개수를 지닌 원소들로 이루어진 집합
• 클릭 사이즈: 클릭 중 최대 정점을 가진 원소의 크기 (최대로 겹치는 구간의 크기)

구간 그래프 예시

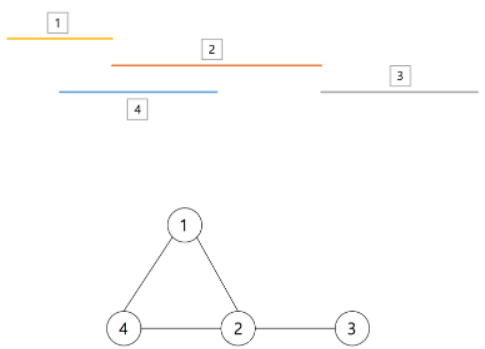
독립 집합: {1,3}, {4,3}
최대 독립 집합: {1,3}, {4,3}
클릭: {1,2,4}, {1,2}, {1,4}, {2,4}, {3,4}
최대 클릭: {1,2,4}
클릭 사이즈: 3

클릭 사이즈 알고리즘

클릭 사이즈를 구하는 알고리즘은 간단하다.

구간의 시작점을 만나면 +1을 하고 끝점을 만나면 -1을 하는 것이다.
그러나 구간을 폐구간, 개구간으로 나눈다면 좀 더 생각을 해야 된다.

구간이 폐구간이면 시작점부터 계산한다.
시작점을 먼저 보고 +1을 해서 교차한다고 알린 다음
끝점을 보고 -1을 해서 구간이 끝났음을 알린다.

구간이 개구간이면 끝점부터 계산한다.
끝점을 먼저 보고 -1을 해서 구간이 끝남을 알린 다음
시작점을 보고 +1을 해서 구간이 시작됨을 알린다.

하지만 첫 번째 그림처럼 개구간, 폐구간이 섞여 있는 경우 헷갈릴 수 있기 때문에
개구간의 시작잠과 끝점에 eps(0이랑 아주 근접한 수)를 더하거나 뺀 다음 폐구간으로 만드는 것도 방법이다.

이렇게 수치를 업데이트하면서 수치가 가장 컸을 때의 값이 클릭 사이즈가 된다.

이 알고리즘으로 문제를 풀면 예시(첫 번째 그림)의 정답은 3이 된다.

최대 클릭 알고리즘

클릭 사이즈 로직을 이해했다면 최대 클릭을 알아내는 것은 쉽다.

각 구간의 시작점과 끝점을 거치면서 클릭 사이즈를 구하게 되는데
점들을 거칠 때마다 MAX(현재 최대 수치, 갱신한 수치)를 계산해서 현재 최대 수치를 업데이트하는 것이다.
여기서 주의할 점은 MAX를 업데이트할 때 해당 점의 x좌표도 같이 저장하는 것이다.

예를 들어 (현재 최대 수치:3, x:10) -> (현재 최대 수치:4, x:12) 이런 식으로 말이다.
이제 최종 x값을 포함하는 구간들이 최대 클릭이 된다.

최대 클리크 구하기: https://www.acmicpc.net/problem/13160

최대 독립 집합 알고리즘

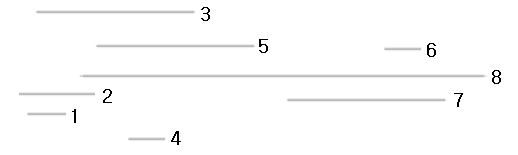
최대 독립 집합이 이미 있다고 가정하자.
예를 들어 {2,5,6}이라는 최대 독립 집합 A가 있다고 하자.

집합 A의 구간 중 가장 앞 쪽에 위치한 구간(2)의 끝점은 전체 구간 중 끝점이 가장 작은 구간의 끝점보다 항상 크거나 같다. 따라서 집합 A에서 구간(2)를 빼고 구간(1)을 넣어도 지장이 없다.

즉 최대 독립 집합을 구할 때 끝점이 가장 작은 구간은 항상 포함될 수 있다.

그러므로 이 알고리즘의 첫 번째 로직은 ‘끝점이 가장 작은 구간(1)을 선택하는 것‘이다.

이후 구간(1)과 교차하는 모든 구간(2,3)은 삭제한다.
그럼 교차하지 않는 구간만 남게 될 것이다.

이 남은 구간들(4,5,6,7,8) 기준으로 다시 최대 독립 집합 문제를 푸는 것이다.
그럼 결국 순환 문제가 된다.

1. 끝점이 가장 작은 구간을 선택한다.
2. 끝점이 가장 작은 구간과 교차하는 구간들을 삭제한다.
3. 나머지 구간들 중 최대 독립 집합을 찾는다. (순환으로 해결)

이 알고리즘으로 문제를 풀면 정답은 {1,4,6}이 된다.
교차하는 구간을 찾는 작업이 O(n)이고 이러한 작업을 순환할 때마다 하니까
시간 복잡도는 O(n²)이 된다.

그런데 가장 끝점이 작은 구간을 선택하면서 겹치지 않도록 하는 것이 Key Point면
처음부터 정렬을 하면 더 편하지 않을까?

따라서 개선된 알고리즘은 이렇다.

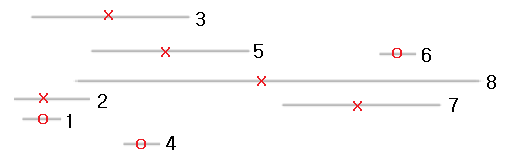
1. 구간들을 끝점을 기준으로 정렬한다.
2. 가장 끝점이 작은 구간을 선택한다.
3. 그 다음으로 작은 구간을 살펴 보는데 이전에 선택한 구간과 겹치지 않으면 선택한다.
겹치면 pass하고 다음 구간을 살펴 본다. (반복)

ex) 구간1 선택 -> 구간2는 구간1과 비교하고 pass -> 구간3은 구간1과 비교하고 pass -> 구간4는 구간1과 비교하고 선택 -> 구간5는 구간4와 비교하고 pass -> 구간6은 구간4와 비교하고 선택 -> 구간7은 구간6과 비교하고 pass -> 구간8은 구간6과 비교하고 pass

이 방식은 전체 구간과 비교할 필요가 없고 이전에 선택한 구간 한 개만 비교하면 된다.
즉 모든 구간에 대하여 1번만 비교하니 O(n)을 만족한다.

정렬 시간을 합쳐서 시간 복잡도를 계산하면 O(nlogn)이 된다.

정점 채색 알고리즘

정점 채색을 할 때는 클릭 사이즈 만큼의 색이 필요하다. 최대로 겹칠 때 색이 부족하면 안 되기 때문이다.

정점 채색의 알고리즘은 다음과 같다.

1. 구간들을 시작점을 기준으로 정렬한다. 이후 클릭 사이즈 만큼의 색을 준비한다.

2. 첫 번째 구간부터 색을 전부 사용할 때까지 랜덤으로 색칠하고 끝점에 해당 색을 나타낸다.

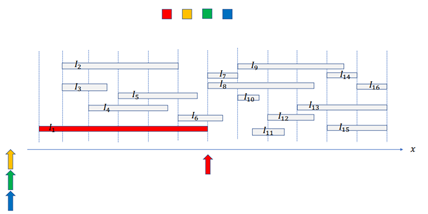
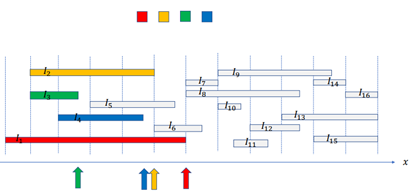
3. 가장 왼쪽에 위치한 색(초록)으로 다음 구간을 색칠하고 끝점에 해당 색을 나타낸다.

4. 모든 구간을 전부 색칠할 때까지 (3) 과정을 반복한다.

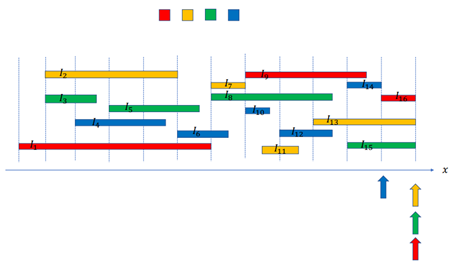
이 로직만 보면 왜 가장 왼쪽 색을 선택해도 문제가 없는지 의문이 들 수 있다.
이것을 귀류법으로 증명하겠다.

가장 왼쪽 색(초록)을 선택했을 때 문제가 생긴다고 가정해 보자.
정점 채색에서 문제가 생긴다는 의미은 인접한 구간에 같은 색이 색칠된다는 것이다.
이 말은 초록색을 선택하면 I3의 끝점이 I5의 시작점보다 커지거나 I5의 시작점이 I3의 끝점보다 작아져서 두 인접한 구간이 같은 색으로 색칠된다는 것이다. 또한 구간에 변화가 생겨 클릭 사이즈도 k+1이 된다.
이런 말도 안 되는 상황이 발생한 이유는 가정이 틀렸기 때문이다.
따라서 가장 왼쪽 색을 선택해도 문제가 생기지 않는다.

다음은 구현 방법이다.

화살표(색칠된 구간의 끝점)를 Heap에 저장한다.
Heap에 저장하면 deleteMin() 함수로 가장 작은 화살표를 찾을 수 있다.
또한 insert() 함수로 화살표를 올바른 위치에 삽입할 수 있다.

클릭 분할 알고리즘

클릭 분할 알고리즘은 최대 독립 집합 알고리즘과 유사하다.

1. 구간들을 끝점을 기준으로 정렬한다.
2. 가장 끝점이 작은 구간을 선택한다.
3. 그 다음으로 작은 구간을 살펴 보는데 이전에 선택한 구간과 겹치지 않으면 선택한다.
겹치면 저장하고 다음 구간을 살펴 본다. (반복)

즉 최대 독립 집합 알고리즘은 겹치는 구간을 버렸다면
클릭 분할 알고리즘은 겹치는 구간을 저장하는 셈이다.