위상 정렬: 순서가 정해져있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용되는 알고리즘

ex) 1->4->0->2->3->5

방향 그래프를 대상으로 위상 정렬을 하기 위한 알고리즘

진입 차수를 이용하는 알고리즘이다.
진입 차수란 각 정점에 들어오는 에지의 수를 의미한다.

먼저 진입 차수가 0인 정점을 선택하고, 선택된 정점과 여기에 부착된 모든 에지를 삭제한다.
이와 같은 진입 차수 0인 정점의 선택과 삭제 과정을 반복해서 모든 정점이 선택/삭제되면 알고리즘이 종료된다.
진입 차수가 0인 정점이 여러 개 존재할 경우 어느 정점을 선택해도 무방하다. (복수의 위상 순서가 존재)

c언어 구현에서 in_degree배열은 모든 정점의 진입 차수에 해당한다.
위 그림을 예시로 들면 {0,0,1,3,1,3}이 저장된다.

진입 차수가 0인 정점을 선택하면 스택에 push하고
(선택된 정점과 여기에 부착된 모든 에지를 삭제하는 과정)은
(스택에서 pop하는 것), (in_degree배열을 수정하는 것)으로 대체한다.
에지를 삭제하는 것을 진입 차수를 줄이는 것으로 대체하는 것이다.
in_degree배열을 수정해서 진입 차수가 0인 정점이 나오면 다시 push하는 구조이다.

시간복잡도: O(n+m), n은 정점의 개수, m은 에지의 개수

#include <stdio.h>
#include <stdlib.h>

#define max 100

typedef struct {
	int top;
	int stack[max];
}stack_type;
typedef stack_type* stack_type_ptr;

void init(stack_type_ptr s) {
	s->top = -1;
}

int is_full(stack_type s) {
	if (s.top == max - 1)
		return 1;
	else
		return 0;
}

int is_empty(stack_type s) {
	if (s.top == -1)
		return 1;
	else
		return 0;
}

int pop(stack_type_ptr s) {
	if (!is_empty(*s)) {
		int tmp = s->stack[s->top--];
		return tmp;
	}
	else
		printf("스택이 비어 있음");
}
void push(stack_type_ptr s, int item) {
	if (!is_full(*s)) {
		s->top++;
		s->stack[s->top] = item;
	}
	else
		printf("스택이 꽉 참");
}

int peek(stack_type s) {
	if (!is_full(s)) {
		int tmp = s.stack[s.top];
		return tmp;
	}
	else
		printf("스택이 꽉 참");
}

typedef struct GraphNode {
	int vertex;
	struct GraphNode* link;
}GraphNode;

#define MAX_VERTICES 50

typedef struct GraphType {
	int n; // 정점의 개수
	GraphNode* adj_list[MAX_VERTICES];
}GraphType;

// 그래프 초기화
void graph_init(GraphType* g) {
	int v;
	g->n = 0;
	for (v = 0; v < MAX_VERTICES; v++)
		g->adj_list[v] = NULL;
}

// 정점 삽입 연산
void insert_vertex(GraphType* g, int v) {
	if ((g->n) + 1 > MAX_VERTICES) {
		fprintf(stderr, "그래프: 정점의 개수 초과");
		return;
	}
	g->n++;
}

// 간선 삽입 연산, v를 u의 인접 리스트에 삽입한다.
void insert_edge(GraphType* g, int u, int v) {
	GraphNode* node;
	if (u >= g->n || v >= g->n) {
		fprintf(stderr, "그래프: 정점 번호 오류");
		return;
	}
	if (g->adj_list[u] == NULL) { // insert_first
		node = (GraphNode*)malloc(sizeof(GraphNode));
		node->vertex = v;
		node->link = g->adj_list[u];
		g->adj_list[u] = node;
	}
	else { //insert_last
		node = g->adj_list[u];
		while (node->link != NULL)
			node = node->link;
		node->link = (GraphNode*)malloc(sizeof(GraphNode));
		node->link->vertex = v;
		node->link->link = NULL;
	}
}

// 위상정렬
int topo_sort(GraphType* g) {
	int i;
	stack_type s;
	GraphNode* node;

	// 모든 정점의 진입차수를 계산
	int* in_degree = (int*)malloc(g->n * sizeof(int));
	for (i = 0; i < g->n; i++)
		in_degree[i] = 0;
	for (i = 0; i < g->n; i++) {
		node = g->adj_list[i]; // 정점 i
		while (node != NULL) {
			in_degree[node->vertex]++; // 진입차수[정점 i와 인접한 정점]+1
			node = node->link;
		}
	}
	
	// 진입차수가 0인 정점을 스택에 삽입
	init(&s);
	for (i = 0; i < g->n; i++) {
		if (in_degree[i] == 0) {
			push(&s, i);
		}
	}

	// 위상 순서 생성으로 처리된 정점의 개수 
	int num = 0; 

	// 위상 순서를 생성
	while (!is_empty(s)) {
		int w;
		w = pop(&s);
		printf("정점 %d ->", w); // 정점 출력
		// 인접한 정점(들)의 진입 차수를 변경
		node = g->adj_list[w];
		while (node != NULL) {
			in_degree[node->vertex]--; // 진입차수[정점 i와 인접한 정점]-1
			// 변경하고 진입차수가 0이 되면 스택에 삽입
			if (in_degree[node->vertex] == 0)
				push(&s, node->vertex);
			node = node->link;
		}
		num++;
	}
	free(in_degree);

	// 모든 정점을 처리했으면 마지막 'end'를 출력 
	if(num==g->n)
		printf("end\n");

	// 사이클이 아니면 True 반환 (num이 g->n이면 모든 정점 처리 -> 사이클 x) 
	return (num==g->n); 
}

int main(void) {
	GraphType g;

	graph_init(&g);
	insert_vertex(&g, 0);
	insert_vertex(&g, 1);
	insert_vertex(&g, 2);
	insert_vertex(&g, 3);
	insert_vertex(&g, 4);
	insert_vertex(&g, 5);

	// 정점 0의 인접 리스트 생성
	insert_edge(&g, 0, 2);
	insert_edge(&g, 0, 3);
	// 정점 1의 인접 리스트 생성
	insert_edge(&g, 1, 3);
	insert_edge(&g, 1, 4);
	// 정점 2의 인접 리스트 생성
	insert_edge(&g, 2, 3);
	insert_edge(&g, 2, 5);
	// 정점 3의 인접 리스트 생성
	insert_edge(&g, 3, 5);
	// 정점 4의 인접 리스트 생성
	insert_edge(&g, 4, 5);

	//위상정렬
	topo_sort(&g);

	return 0;
}

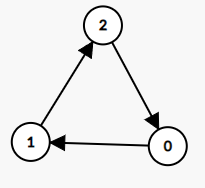
그래프에 남아 있는 정점 중 진입 차수가 0인 정점이 없다면 사이클이기에 위상 정렬 알고리즘은 중단된다.
(모든 정점에 대해 위상 순서 생성을 못하면 사이클)

따라서 위상정렬은 사이클 판단 여부로도 많이 사용된다.

int main(void) {
	GraphType g;

	graph_init(&g);
	insert_vertex(&g, 0);
	insert_vertex(&g, 1);
	insert_vertex(&g, 2);

	// 사이클 생성 
	insert_edge(&g, 0, 1);
	insert_edge(&g, 1, 2);
	insert_edge(&g, 2, 0);

	// 사이클 확인
	if(!topo_sort(&g))
		printf("find cycle graph!!\n");

	return 0;
}