동적계획법(DP)은 ‘컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술’입니다.

이를 쉽게 말하면 아래와 같습니다.

‘작은 문제에 대한 답을 배열에 저장하고, 큰 문제를 풀 때 이 배열을 이용함으로
써 작은 문제를 여러 번 푸는 것을 막는 기법’

이제 카탈랑 수로 동적계획법(DP)의 필요성을 알아 보겠습니다.

카탈랑 수는 ‘n개의 내부 노드와 n+1개의 외부 노드를 가진 이진 트리의 개수’입니다.
이 수의 의미에 집중하지 말고 DP에 집중해봅시다.

카탈랑 수의 점화식은 아래와 같습니다.

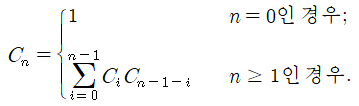
Cn을 구하기 위해서는 Ci (i=0,1,..n-1)를 풀어야 하는 구조입니다.
[ Cn: 큰 문제, Ci:작은 문제 ]

이 문제를 단순하게 재귀적 방법으로 코딩하였습니다.

int catalan(int n) {
	if (n==0)
	    return 1;
	int Cn = 0;
	for (int i = 0; i <= n - 1; i++) 
	    Cn += catalan(i) * catalan(n-1-i);
	
	return Cn;
}

예시로 n=4인 문제(C4)를 분석해보겠습니다.

n=4인 문제를 풀기 위해서는 n=0~3에 대한 답이 필요합니다.
(catalan(i): n=i에 대한 답, Ci)

다시 n=3인 문제를 풀기 위해서는 n=0~2에 대한 답이 필요합니다.
다시 n=2인 문제를 풀기 위해서는 n=0~1에 대한 답이 필요합니다.
다시 n=1인 문제를 풀기 위해서는 n=0에 대한 답이 필요합니다.

이것을 트리 형태로 그려보면 구해야 하는 답의 개수(풀어야 하는 문제의 개수)를 알 수 있습니다.

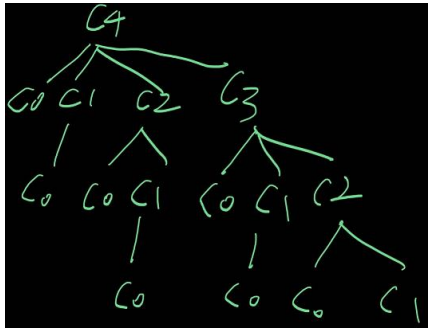
n=0일 때는 0개,
n=1일 때는 1개,
n=2일 때는 (1+2)개,
n=3일 때는 (1+2+3)개를 풀어야 하니
총 10(1+3+6)개의 문제를 풀어야 합니다.

문제의 개수를 시그마로 표현하면 아래와 같습니다.

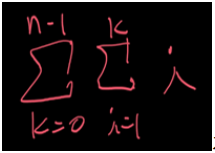
n=100이면 166650개를, n=1000이면 1억개가 넘는 문제를 풀어야 합니다.

한 문제 당 연산을 한 번만 한다고 가정해도,
1초에 1억번 연산하는 컴퓨터가 고작 n=1000인 문제를 1초안에 해결하지 못하니 정말 효율성이 없다고 말할 수 있습니다.

하지만 n=0~3까지 구한 답을 배열에 저장한다면 딱 3개의 문제만 풀 수도 있습니다.

n=1인 문제를 풀기 위해 n=0일 때의 답을 이용하고, 답을 배열에 저장합니다.
n=2인 문제를 풀기 위해 n<2일 때의 답(배열 원소)을 이용하고, 답을 배열에 저장합니다.
n=3인 문제를 풀기 위해 n<3일 때의 답(배열 원소)을 이용하고, 답을 배열에 저장합니다.

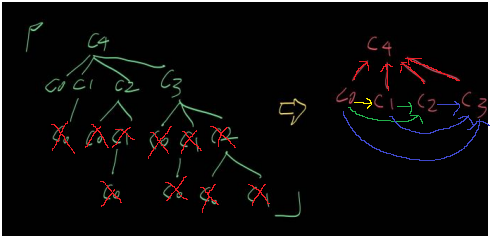
이번에는 이 DP를 이용한 방법으로 코딩해보았습니다.

int catalan(int n) {
	int* C = (int*)calloc(n+1,sizeof(int));
	C[0] = 1;
	for (int k = 1; k <= n; k++) {
		for (int i = 0; i <= k-1; i++) {
			C[k] += C[i] * C[k - 1 - i];
		}
	}
	return C[n];
}

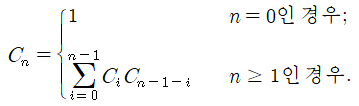
카탈랑 수 점화식을 다시 확인해봅시다.

C[n]을 알기 위해서는 C[0]~C[n-1]에 대한 정보가 필요하다는 의미로도 해석할 수 있습니다.
(C배열: k에 대한 카탈랑 수가 저장됨, 0<=k<=n )

그래서 입력한 n에 대하여 C[k] (0<=k<=n)를 구하는 작업을 진행하였습니다.

점화식에 의해 C[0]은 1이 저장됩니다.

k가 1부터 n-1까지는 C[0]~C[k-1]를 보고 C[k]를 채워 나가고,
k=n일 때는 C[0]~C[n-1]을 보고 C[n]을 채우게 됩니다.

이렇게 n에 대한 카탈랑 수를 구하기 위해
총 n-1개의 문제(1~n-1)만 풀며 효율적으로 해결하였습니다.

이 프로그램의 시간복잡도를 계산하면
O(n^2)이며 n이 10,000일 때까지 1초안에 해결할 수 있습니다.

n=18에 대하여 두 프로그램의 시간을 비교하면 아래와 같습니다.

이러한 DP는 아래의 두 가지 방법으로 구현할 수 있습니다.

1. 반복문을 통해 (아래->위)로 접근하는 방식: 상향식-접근, Tabulation이라고 부름
(반복문을 통해 dp_table[0]부터 dp_table[n]까지 채워 나가는 구조)

2. 재귀를 통해 (위->아래)로 접근하는 방식: 하향식-접근, Memoizatoin이라고 부름
(재귀를 통해 맨 아래까지 접근한 다음 다시 올라가면서 dp_table[0]~dp_table[n]을 채워 나가는 구조)

(관련 문제)를 소개하며 포스팅을 마치겠습니다.

감사합니다.