CNN은 Convolutional Neural Network입니다.

DNN과는 꽤 다른 구조를 취하고 있습니다.
CNN의 대표적인 특징은 이미지 자체를 입력으로 줄 수 있다는 점입니다.
CNN은 영상 처리에서 좋은 성능을 보입니다.
1. 픽셀의 위, 아래, 좌우 정보 등을 담는 형상 데이터가 유지되기 때문입니다.
(DNN의 입력처럼 flattening하면 형상 데이터가 전부 깨짐)
2. Feature에 영향을 미치는 영역(receptive field)를 기억할 수 있기 때문입니다.
(필터를 영상에 포개서 feature값을 얻었을 때, 그 때에 해당하는 영상 영역)
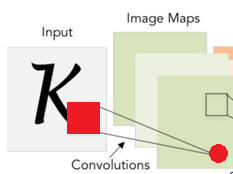
빨간 원: feature, 빨간 사각형: receptive field
Convolution 연산

위 예시는 4×4 입력 영상과 3×3 필터를 이용한 합성곱(convolution) 연산입니다.
1. 영상의 행과 열을 벗어나지 않도록 모든 영역에 필터를 대응시킵니다.
2. 대응시킬 때마다 하다마드 곱셈을 진행합니다.
(=) Hadamard Product(Element-wise): 같은 크기의 두 행렬의 각 성분을 곱하는 연산
3. 더한 값들은 모여서 Feature Map(Activation Map)을 이루게 됩니다.
결국 Feature Map은 필터와 합성곱(convolution) 연산을 통해 나온 feature값들의 모임입니다.

합성곱 연산이 끝났으면 bias를 더해서 결과를 출력합니다.

참고로 결과로 나온 Feature Map의 개수는 필터의 개수와 같습니다.
즉 칼라 영상(32x32x3)에 필터(5x5x3) 1개를 convolution하면 Feature Map의 개수는 1개입니다.
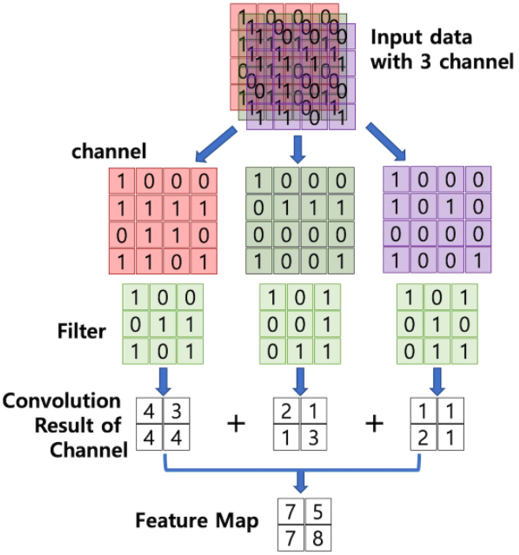
위는 칼라 영상(4x4x3)에 필터(3x3x3) 1개를 convolution하는 예시입니다.
영상과 필터의 채널 수는 항상 동일하며, 각 채널 별로 convolution한 결과를 합친다고 생각하면 됩니다!!
Stride: 보폭
stride는 합성곱 연산 중 필터를 이동하는 폭입니다.

위는 stride가 1인 경우입니다.
픽셀을 한 칸씩 움직이는 것을 확인할 수 있습니다.
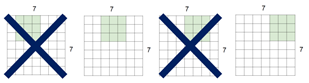
위는 stride가 2인 경우입니다.
픽셀은 항상 두 칸씩 움직이게 됩니다.
stride에 따른 output size는 다음과 같습니다.
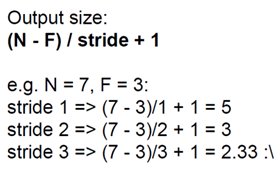
만약 stride가 3과 같이 output size가 정수로 떨어지지 않으면 Fit되지 않습니다.
Padding: 가장자리 처리
padding은 이미지의 가장자리를 처리하는 기법입니다.
가장 자리 픽셀에 필터를 적용하는 경우 두 가지 방법으로 처리할 수 있습니다.
1. valid: 필터를 입력 영상 안에서만 움직이게 합니다. 즉 필터를 영상 외부에 나가지 못하게 합니다. 결국 가장 자리 픽셀은 아예 처리하지 않습니다. 컨볼루션이 진행될수록 출력은 점점 작아집니다.

2. same: 입력 영상의 주변을 특정값으로 채웁니다. 0으로 채우는 것을 제로-패딩이라고 합니다. 패딩을 적용하면, 컨볼루션 후에 입력과 출력의 크기는 같아집니다.
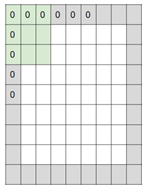

pad와 stride에 따른 output size는 다음과 같습니다.

다음은 stride와 padding에 대한 문제입니다.
Input volume: 32x32x3, 10개의 5×5 filters with stride 1, pad 2일 때 Output Volume은?
A. (32+2*2-5) / 1 +1 = 32 -> 32×32, 이것이 10개 -> 32x32x10
Hyperparameter(학습을 위해 사용자가 설정해줘야 하는 값)의 표현은 다음과 같습니다.
K: 필터의 수
F: 필터의 사이즈
S: 스트라이드
P: 제로 패딩을 한 횟수
Number of Parameters(필터의 weight + bias 수)는 다음과 같습니다.
–> F^2*C*K +K biases // (F^2*C + 1) x K
(C: 입력 영상의 채널 수)
Input volume: 32x32x3, 10개의 5×5 filters with stride 1, pad 2일 때 Num of Parameters은?
A. (5x5x3)(weight) + 1(bias) = 76, 이것이 10 개 -> 76 x 10 = 760개
Pooling 연산
pooling은 Feature Map의 크기를 줄이는 연산입니다.
pooling은 두 가지 방법이 있습니다.
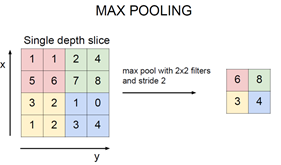
1. MAX POOLING
풀링 필터를 Feature Map에 포개었을 때, 가장 큰 픽셀 값만 택합니다.
Max pooling을 하는 이유는 여러 가지가 있습니다.
1. 숫자가 클수록 학습에 기여하는 정도도 크기 때문에 큰 것만 남기는 것이다.
2. 풀링 후 레이어의 크기가 작아지므로 계산이 빨라진다.
3. 입력 변화에 영향을 적게 받는다. (robust하다)

2. AVG POOLING
풀링 필터를 Feature Map에 포개었을 때, 평균 값을 택합니다.
풀링은 MAX POOLING이 주로 쓰이게 됩니다.
CNN 구조
지금까지 CNN연산에서 가장 중요한 (컨볼루션, 풀링)을 알아 보았습니다.
CNN 네트워크의 구조는 여러 컨볼루션 레이어와 풀링 레이어로 이루어 집니다.
추가로 RELU연산과 FC레이어도 쓰이게 됩니다.
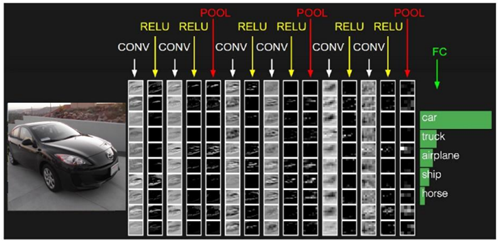
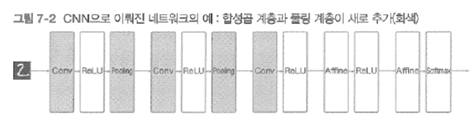
이렇게 (CONV-RELU-POOLING) 레이어를 CRP라고 간단하게 부르기도 합니다.
만약 네트워크를 깊게 해서 더 자세한 특징을 찾고 싶으면 padding을 계속 same으로 하면 됩니다.
그렇지 않고 네트워크를 얕게 하고 싶다면 stride를 크게 해서 output size를 줄이면 됩니다.
하지만 실제로 CNN 네트워크를 사용자가 구성하는 일은 적습니다.
왜냐하면 이미 좋은 CNN Architecture가 발표되었기 때문입니다.
따라서 우리는 에러율이 적은 CNN Architecture를 그대로 이용해도 됩니다.
추가 개념
1. 1×1 CONV는 채널의 데이터만 압축시키고(합치고) 싶을 때 사용합니다.
아래는 입력 영상(56x56x64)에 필터(1x1x64) 32개를 컨볼루션해서 feature map(56x56x32)를 얻는 모습입니다.

2. 필터를 여러 개 이용하면 같은 영역을 보지만 다른 Feature를 얻어 냅니다.
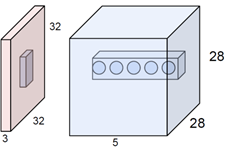
아래는 입력 영상(32x32x3)에 필터(5x5x3) 5개를 컨볼루션해서 feature map(28x28x5)를 얻는 모습입니다.
3. 필터도 Receptive Field라고 볼 수 있습니다.
Receptive Field는 Feature에 영향을 미치는 영역입니다.
필터가 없었으면 Feature는 나올 수 없습니다.

영상처리와 CNN
영상 처리에서는 필터의 가중치가 미리 결정됩니다.
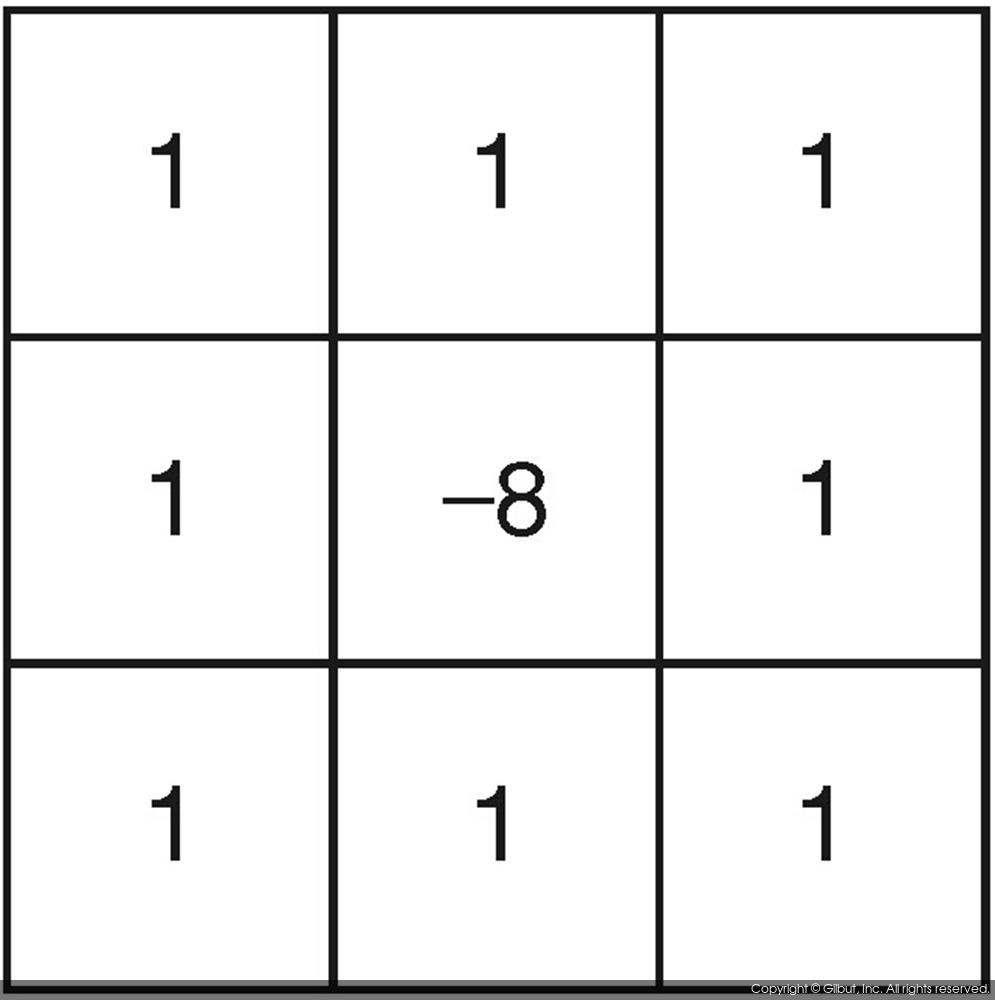
예를 들어 라플라시안 필터(엣지 검출용 필터)는 항상 위와 같은 가중치를 지닙니다.
하지만 컨볼루션 신경망에서는 필터의 가중치가 미리 결정되는 것이 아닙니다.
랜덤 상태에서 출발하여서 샘플(Target Vector)을 이용한 훈련 과정을 통하여 필터의 가중치가 자동으로 결정됩니다.
예를 들어 ‘3’이라는 이미지가 왔을 때,
랜덤 상태에서 출발하여서 원 핫 코딩된 (001:분류-3)을 보고 필터의 가중치를 역으로 결정하는 것입니다.
이 과정이 바로 CNN의 Backpropagation입니다.

즉 어떤 특징을 추출하려고 특정한 가중치를 가지는 필터를 미리 만드는 것이 아닙니다.
CNN에서 어떤 컨볼루션 필터가 어떤 특징을 추출하는지는 알 수 없습니다.
감사합니다.
