항상 시간복잡도가 O(nlogn)을 만족하는 ‘합병 정렬’을 알아 봅시다!
합병 정렬은 다음의 단계들로 이루어 집니다.
1. 분할(Divide): 입력 배열을 2개의 부분 배열로 분할한다.
2. 정복(Conquer): 부분 배열들을 정렬한다.
3. 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 통합한다.
즉 작은 문제를 풀어서 큰 문제를 해결하는데 사용하는 분할-정복법입니다.
그림을 통한 예시로 설명하겠습니다.
분할(Divide)
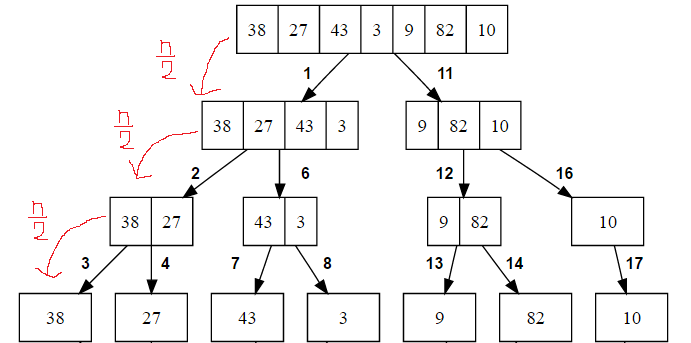
(크기가 n인 배열)을 (크기가 n/2인 두 부분 배열)로 분할하는 과정입니다.
순환 호출을 이용해서 부분 배열의 크기가 충분히 작을 때까지 만듭니다.
정복(Conquer) 및 결합(Combine)
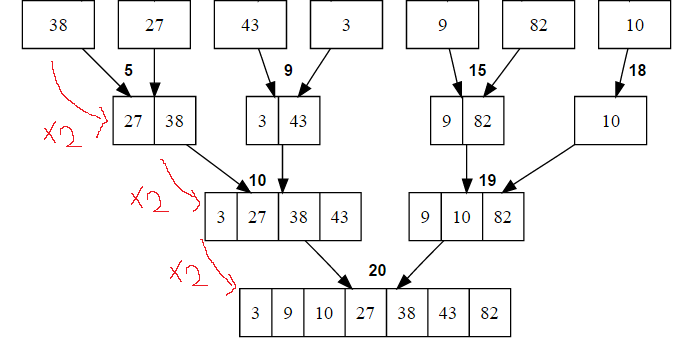
부분 배열들을 정렬과 동시에 합병을 하는 과정입니다.
합병을 하면 할수록 부분배열의 크기가 2배씩 커지는 것을 확인할 수 있습니다.
정렬-합병을 자세히 살펴보면 다음과 같습니다.

왼쪽 부분배열을 A, 오른쪽 부분배열을 B라고 하겠습니다.
각 부분배열은 인덱스에 해당하는 i와 j가 있습니다.
A배열과 B배열 밑에 있는
크기가 A+B인 배열은 C라고 하겠습니다.
이제 A[i]와 B[j]를 비교해서 작은 값을 C배열에 차곡차곡 넣습니다.
만약 A[i]가 더 작으면 A[i]를 넣고 i를 1만큼 증가시킵니다.
그렇지 않고 B[j]가 더 작으면 B[j]를 넣고 j를 1만큼 증가시킵니다.
이 과정을 계속 하면 i와 j 중 한 인덱스는 배열의 크기와 같게 됩니다.
만약 i가 배열의 크기가 되면 B배열만 남아 있으니 남은 B배열의 원소를 C배열에 넣습니다.
그렇지 않고 j가 배열의 크기가 되면 A배열만 남아 있으니 남은 A배열의 원소를 C배열에 넣습니다.
위의 과정을 통해 두 부분배열의 정렬과 합병을 동시에 할 수 있습니다.
이제 분할과 합병 과정을 한 번에 살펴 보면 아래의 그림처럼 만들어 집니다.
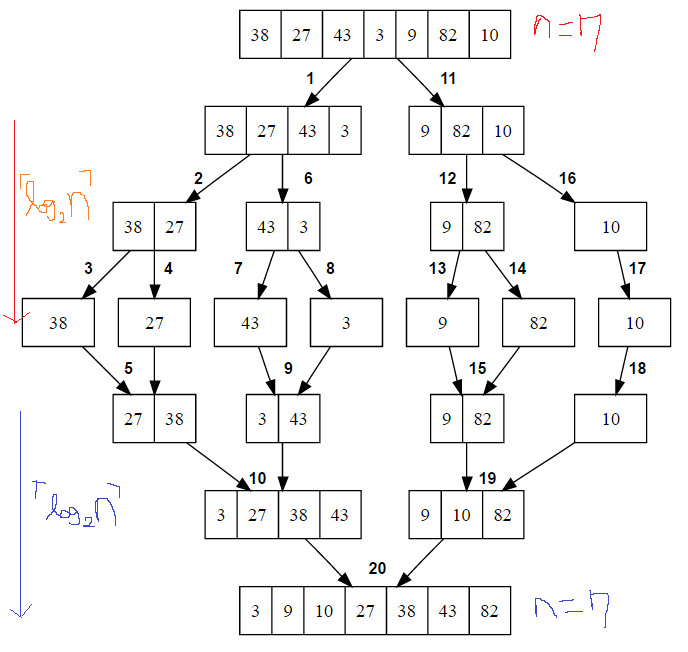
분할을 할 때는 배열의 크기가 n에서 1/2배씩 계속 줄고
합병을 할 때는 배열의 크기가 1에서 2배씩 계속 늘어 납니다.
따라서
분할을 해서 크기가 1이 되기까지 ceil(log2n) 개의 과정이 있게 되고
합병을 해서 크기가 n이 되기까지 ceil(log2n) 개의 과정이 있게 됩니다.
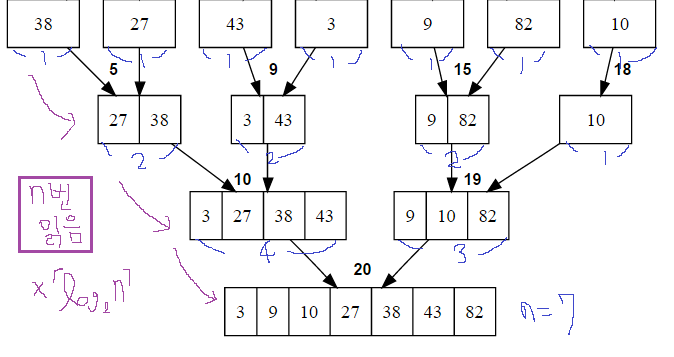
참고로 한 과정 당 n개의 데이터를 읽고 정렬-합병을 하는 작업을 합니다.
이 과정이 ceil(log2n)개 있으니 총 n * ceil(log2n)번 데이터를 읽게 됩니다.
데이터를 읽고 작업하는 만큼 시간이 소요되니, 이를 시간복잡도로 나타내면
O(nlogn)이 됩니다.
따라서 이 알고리즘은 항상 O(nlogn)을 만족하는 좋은 정렬이라고 볼 수 있습니다.
지금까지 설명한 내용을 코드로 나타내겠습니다!!
#define MAX 100
int sorted[MAX];
void merge(int list[], int left, int mid, int right) {
int i, j, k;
i = left; // 오른쪽 Part의 시작 위치
j = mid + 1; // 왼쪽 Part의 시작 위치
k = left; // 정렬될 리스트의 시작 위치
// 작은 순서대로 합병 (오른쪽 or 왼쪽 Part가 전부 복사될 때까지)
while (i <= mid && j <= right) {
if (list[i] <= list[j])
sorted[k++] = list[i++];
else
sorted[k++] = list[j++];
}
// 남은 요소 일괄 복사 (오른쪽 Part)
if (i > mid) {
for (int idx = j; idx <= right; idx++)
sorted[k++] = list[idx];
}
// 남은 요소 일괄 복사 (왼쪽 Part)
else {
for (int idx = i; idx <= mid; idx++)
sorted[k++] = list[idx];
}
// sorted 배열 내용을 list로 복사
for (int idx = left; idx <= right; idx++)
list[idx] = sorted[idx];
}
void merge_sort(int list[], int left, int right) {
int mid;
// 부분배열의 크기가 1이상이면 동작 -> list의 크기가 2이상이면 동작
if (left < right) {
mid = (left + right) / 2;
merge_sort(list, left, mid); // 최종 결과 -> 오른쪽 배열 정렬
merge_sort(list, mid + 1, right); // 최종 결과 -> 왼쪽 배열 정렬
merge(list, left, mid, right); // 오른쪽 배열과 왼쪽 배열 합병
}
}
merge함수부터 살펴 보겠습니다.
merge함수는 (정복-결합) 부분에 해당합니다.
하나의 배열(list) 안에 두 개의 정렬된 부분 배열이 저장되어 있다고 가정합니다.
즉 첫 번째 부분 배열은 list[left]부터 list[mid]까지 이고,
두 번째 부분 배열을 list[mid+1]부터 list[right]까지입니다.
그리고 합병된 배열을 임시로 저장하기 위해 sorted라는 배열을 사용했습니다.
이 임시 배열(sorted)에 정렬된 값들을 다시 원래 배열(list)에 복사했습니다.

이번엔 merge_sort함수를 살펴 보겠습니다.
merge_sort에서는
주어진 배열을 2등분하고, 각각의 부분 배열에 대하여 다시 merge_sort함수를 순환 호출합니다.
이 과정을 부분 배열의 크기가 1이 될 때까지 반복합니다.
정확히 말하면 list가 list[left=mid]와 list[right=mid+1]로만 이루어 져서 list에 저장된 두 개의 부분 배열의 크기가 1이 될 때까지 반복합니다.
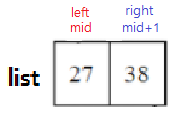
위처럼 두 부분 배열의 크기가 1이 되면 merge함수를 호출해서 (정복-결합)을 진행합니다.
다음에는 재귀적 성질에 의해 두 부분 배열의 크기가 1인 또 다른 list에 대해 (정복-결합)을 진행합니다. ex) [3,48]
이후에는 재귀적 성질에 의해 크기가 2배인 두 부분 배열에 대해서 (정복-결합)을 진행합니다. ex) [27,38,3,48]
최후에는 크기가 n인 원래 배열로 (정복-결합)이 되면서 함수가 종료됩니다.
