터틀 GUI 생성

import turtle
T=turtle.Turtle()
turtle.mainloop()

turtle은 파이썬에서 그림을 그려주는 모듈입니다.
이 모듈에서 핵심은 GUI로 나타나는 ‘터틀’입니다.

‘터틀’은 윈도우 창에서 ‘>‘ 형태로 나타납니다.
이 터틀이 움직이면서 선을 그리는 것을 이용하면 원하는 형태를 만들 수 있습니다.

사용법은 turtle모듈의 Turtle클래스로 객체를 만듭니다.
이 객체로 터틀을 움직이거나 회전시킬 수 있습니다.

turtle모듈의 mainloop함수가 소스 마지막에 위치해야 정상적으로 터틀이 움직입니다.

다각형 그리기

import turtle
def polyline(t,n,length,angle):
    for i in range(n):
        # 앞으로 나가면서 그림 
        t.fd(length)
        # angle만큼 돌음
        t.lt(angle)
        
def polygon(t, n, length):
    # n각형은 angle이 360/n임 ex) 4각형은 angle이 90 
    angle = 360 / n
    # length로 앞으로 나아가고 angle만큼 돌리는 것을 n번 반복 
    polyline(t,n,length,angle)
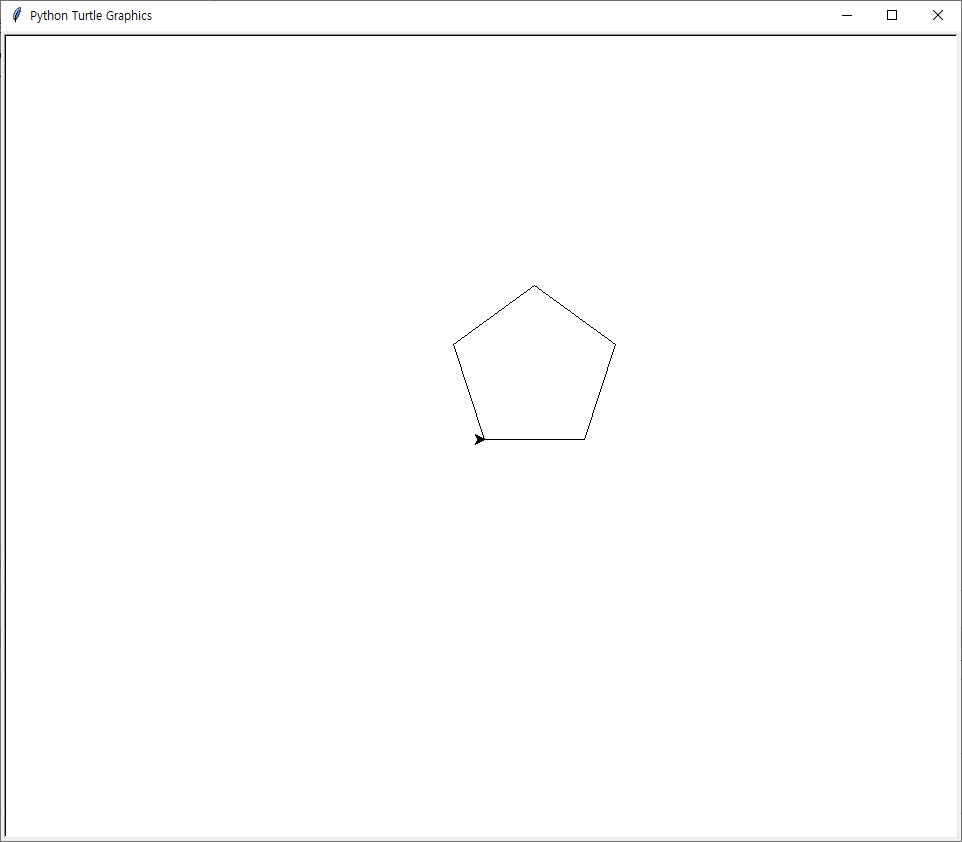
T=turtle.Turtle()
polygon(T,5,100)
turtle.mainloop()

polyline함수부터 알아 보겠습니다. (t는 터틀 객체, n은 반복 수, length는 길이, angle은 회전각)입니다.

fd함수는 터틀을 length길이만큼 앞으로 가게 하는 역할을 합니다.
lt함수는 터틀을 angle도 만큼 돌게 하는 역할을 합니다.

예를 들어 n이 4, angle이 90°, length가 10px이라면,
[10px만큼 앞으로 가고 90° 회전하는 작업]을 4번 시행합니다.
이렇게 ‘정사각형’을 그릴 수 있습니다.

그렇다면 (정)다각형은 이 작업을 n번 시행하면 됩니다.
정사각형을 그리기 위해 angle을 4번 회전해서 앞으로 가게 했다면
정다각형을 그리기 위해 angle을 n번 회전해서 앞으로 가게 하는 것입니다.

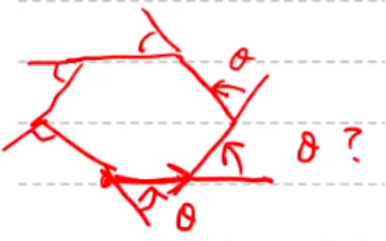
그리고 앞으로 회전각(angle)을 ‘세타(θ)’라고 부르겠습니다.
모든 다각형은 시작점과 끝점이 같기 때문에, 다각형을 그리기 위해 θ 만큼 n번 회전하면 원점으로 돌아와야 합니다.
다시 말해서 θ 만큼 n번 회전하면 360도를 돌아야 합니다.
따라서 θ x n =360을 만족합니다.

결론은 다각형을 그리기 위해 필요한 θ = 360/n이 됩니다.
이제 polyline(t,n,length,360/n)을 호출하면 됩니다.

이 개념을 Encapsulation한 것이 polygon 함수입니다.

다각형으로 원 그리기

import turtle
import math
def polyline(t,n,length,angle):
    for i in range(n):
        # 앞으로 나가면서 그림 
        t.fd(length)
        # angle만큼 돌음
        t.lt(angle)
        
def polygon(t, n, length):
    # n각형은 angle이 360/n임 ex) 4각형은 angle이 90 
    angle = 360 / n
    # length로 앞으로 나아가고 angle만큼 돌리는 것을 n번 반복 
    polyline(t,n,length,angle)
def circle(t,r):
    circumference=2*math.pi*r
    # 3px을 length를 가진다고 생각하고 n각형을 구함 -> 원주로 나누면 됨
    # 분자가 3px보다 작으면 0이 되니 1을 더함 -> 원주가 엄청 작으면 그냥 1각형
    n=int(circumference/3)+1
    # n각형(도형을 그릴 때 끊기는 부분이 n개)일 때 length를 다시 구함 (원주에 해당하는 원을 못 만들기 때문) 
    length=circumference/n
    polygon(t,n,length)
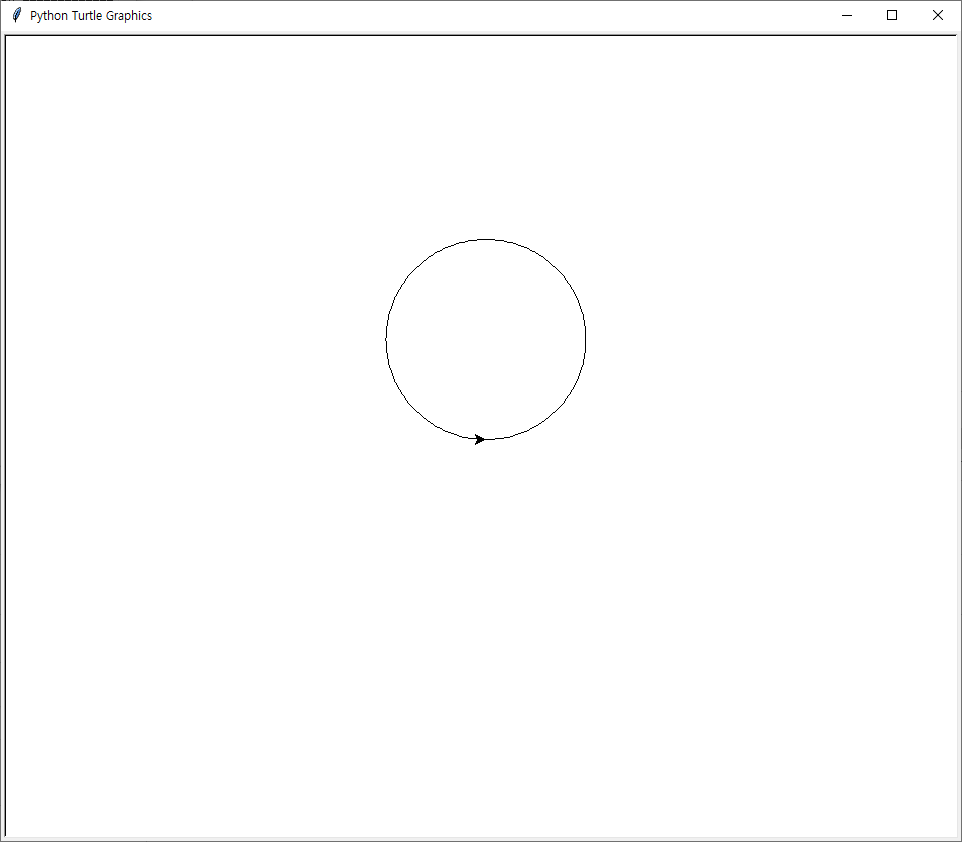
T=turtle.Turtle()
circle(T,100)
turtle.mainloop()

circle 함수를 알아 보겠습니다. (t는 터틀 객체, r은 원의 반지름)입니다.

일단 원주(원의 둘레)를 구합니다. math 모듈로 2*pi*r을 구하면 됩니다.

원은 변이 아주 많은 정다각형이라고 생각할 수 있기 때문에 polygon함수를 이용합니다.
아래 그림은 정이십각형인데, n(변)이 클수록 원과 비슷해지는 개념을 이용한 것입니다.

3px를 임의 length라고 생각하겠습니다.
3px은 도형 한 변의 길이가 되고 도형의 둘레(전체 변의 길이 합)는 위에서 이미 구했습니다.
따라서 (원주/3)개의 변으로 원을 만들 수 있습니다.
파이썬 코드에서는 (원주/3)를 정수형으로 만들었을 때 0이 되는 것을 대비해서 1을 더했습니다.

그런데 변의 개수에 해당하는 n에 3을 곱하면 과연 원주가 나올까요? (3*n=원주?)
다시 말해 3px로 n개의 변을 그려서 구한 원주가 처음 원주 값이 될까요?

n이 int형으로 변환되는 과정에서 소수 부분이 날라가서 문제가 생길 수 있습니다.
예를 들어 원주가 100이라면 33각형이 만들어지는데 원래 원주의 길이와 1px이 부족합니다.

즉 n이 높아져서 원은 그리겠지만, Parameter r로 구한 원주의 원은 만들지 못 합니다.
그래서 원주에 n을 다시 나눠서 length를 다시 구합니다.
그러면 length*n=원주가 되니 문제가 생기지 않습니다.

이렇게 n과 length를 각각 구했으면 polygon(t,n,length)으로 다각형을 그리면 됩니다.

polyline 함수로 호(Arc) 그리기

import turtle
import math
def polyline(t,n,length,angle):
    for i in range(n):
        # 앞으로 나가면서 그림 
        t.fd(length)
        # angle만큼 돌음
        t.lt(angle)
def arc(t,r,angle):
    # 호의 길이 
    arc_length=2*math.pi*r*angle/360
    # 3px을 length를 가진다고 생각하고 몇 번 꺾이는지 구함 
    # 분자가 3px보다 작으면 0이 되니 1을 더함 -> 호의 길이가 엄청 작으면 n=1
    n=int(arc_length/3)+1
    # n은 3px과 매치가 안 되니 n을 기준으로 length를 다시 구함 
    step_length=arc_length/n
    # length만큼 가고 얼만큼 돌아야 하는지 구함 <n각형은 360/n이지만 호니까 angle/n> 
    step_angle=float(angle)/n
    polyline(t,n,step_length,step_angle)
T=turtle.Turtle()
arc(T,100,90)
turtle.mainloop()

arc 함수를 알아 보겠습니다. (t는 터틀 객체, r은 원의 반지름, angle은 호의 각도)입니다.

일단 호의 길이를 먼저 구합니다. math 모듈로 2*pi*r*angle/360을 구하면 됩니다.

호는 원의 일부입니다.
원이 ‘n이 큰 다각형’을 그리는 문제라면,
호는 ‘n이 큰 다각형 일부’를 그리는 문제입니다.

따라서 n과 length를 구하는 것은 원 문제를 풀 때와 동일합니다. (‘호’여서 step_length라고 표현)

하지만 다각형과 회전각(θ) 구하는 방법이 다릅니다.
이제는 θ 만큼 n번 회전하면 호의 각도가 나와야 되기 때문입니다.
호의 각도가 360도라면 θ x n = 360이 되겠지만, 90도라면 θ x n = 90이 돼야 되겠죠.

호의 각도는 사용자가 angle로 제공하니 step_angle(θ) = angle / n을 통해 구하면 됩니다.

이후 polyline(t,n,step_length,step_angle)을 호출해서 step_angle만큼 회전하는 n개의 선을 그리면 됩니다.