구하고자 하는 값이 a일 때, a의 근삿값을 구해보겠습니다.
일단 아래 그림과 같이 f(a)=0을 만족하는 함수 : [f(x)]를 그립니다.

뉴턴의 방법은 위 함수에서 x값이 x0에서 a가 될 때까지 업데이트하는 것입니다.
즉 f(x)=0이 될 때까지 x를 계속 업데이트를 하는 것입니다.
그러기 위해 f(xn)에 접하는 식인 y=f’(xn)(x-xn)+f(xn)을 구하고 xn+1식을 유도합니다.
xn+1은 f’(xn)(x-xn)+f(xn)=0일 때의 x값입니다.
따라서 xn+1=xn-f(xn)/f’(xn)을 만족합니다.
이제 xn+1이 a가 될 때까지(f(xn+1)=0이 될 때까지) 위 식을 반복해서 풀면 됩니다.
ex) x1=x0-f(x0)/f’(x0), f(x1)!=0 -> x2=x1-f(x1)/f’(x1), f(x2)=0 -> x2=answer
이번에는 이 개념을 이용해서 루트a에 대한 근사치를 구해보겠습니다.
f(루트a)=0인 f(x)에 대해서 f(x)=0을 만족하는 xn+1을 찾으면 됩니다.
구하고자 하는 값이 루트a이면 xn+1은 아래 식으로 일반화할 수 있습니다.
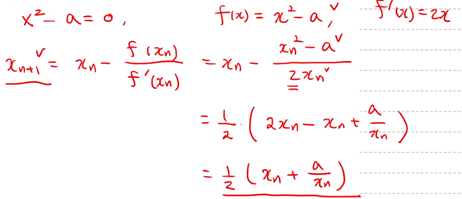
근사치는 아래의 파이썬 코드로 구할 수 있습니다.
import math
def approximate_root(a):
x=a-1
while True:
print(x)
y=(x+a/x)/2
if y==x:
return y
x=y
approximate_root(4)
x는 xn이라고 생각하면 됩니다.
초기 xn은 a-1로 설정하였습니다.
y는 xn+1이라고 생각하면 됩니다.
y값을 구했으면 y(xn+1)값을 x(xn)에 저장합니다. [ xn <- xn+1 ]
xn+1이 더 이상 업데이트가 안 될 때(xn+1=xn)까지 업데이트를 하면 f(x)=0을 만족하는 해를 찾았다는 의미가 됩니다.
하지만 float형 계산을 하는데 equal 연산을 사용하는 것은 위험합니다.
컴퓨터는 무한 소수들을 정확하게 표현할 수 없기 때문입니다. (부동 소수점 오차가 존재)
즉 값이 다른데도 불구하고 같다고 처리할 우려가 있는 것이죠.
x와 y가 정확하게 같은지 여부를 확인하는 대신 내장 함수 abs를 사용해 ‘두 수의 차에 대한 절댓값’만 계산하는 것이 더 안전합니다.
import math
epsilon=1e-6
def approximate_root(a):
x=a-1
while True:
print(x)
y=(x+a/x)/2
if abs(y-x) <epsilon:
return y
x=y
print(approximate_root(4))
따라서 ‘엡실론’이란 것을 이용했습니다.
‘엡실론’은 0과 아주 근접한 수입니다.
y(xn+1)와 x(xn)의 차이가 ‘엡실론’이하일 때 근사치를 구했다고 판정할 수 있습니다.
한 번 a=4, x=3으로 두고 루트4에 대한 근사치를 구해보겠습니다.


One thought on “수학 & 코딩 – 뉴턴의 방법으로 근삿값 구하기”
I love reading through an article that will make people think.
Also, many thanks for allowing for me to comment!