힙을 이용한 허프만 부호화 (텍스트 데이터 압축)

유니코드 문자는 1바이트씩 차지한다. 만약 문자가 10개면 10바이트나 차지하게 된다.
그러나 ‘데이비드 허프먼‘이 제시한 압축 기법에 의하면 10개의 문자를 3바이트 이하로 나타낼 수 있다.

이 압축 기법의 핵심은 빈도 수가 높은 문자에 적은 비트를 할당하고, 빈도 수가 낮은 문자에 많은 비트를 할당하는 것이다.
예를 들어 ‘abccc’라고 하면 a와 b에 각각 11,10 비트를 할당하고 c에 0비트를 할당한다. 이 비트를 문자열에 대입해서 나타내면 (1110000)이므로 7bit로 압축된다.

각 문자에 할당된 비트는 ‘허프만 코드’라고 불리며 ‘허프만 트리’를 통해 얻어 낼 수 있다.
그러기 위해 먼저 ‘허프만 트리’를 구축할 필요가 있다.

‘허프만 트리’에서 리프 노드의 weight는 문자의 빈도 수이다. 내부 노드의 weight는 자식 노드들의 weight합이 된다.
즉 이 트리는 weight를 원소로 가지는 노드가 합쳐 지면서 구축이 된다.
예를 들어 ‘weight=1인 노드’ 와 ‘weight=2인 노드’가 합쳐져서 [(weight가 3인 루트 노드)-(weight가 1,2인 리프 노드들)]형태의 트리가 만들어 진다.

참고로 문자의 빈도 수(weight)가 클수록 나중에 합쳐지게 된다. 따라서 빈도 수가 가장 높으면 트리의 리프 노드들 중 가장 레벨이 낮고 이 낮은 레벨이 적은 ‘허프만 코드’와 연관이 있다.

반대로 문자의 빈도 수(weight)가 낮을수록 먼저 합쳐지게 된다. 초기에는 가장 작은 weight를 지닌 두 개의 노드들로 트리가 구성된다. 이 노드들은 트리의 리프 노드들 중 가장 레벨이 높고 많은 ‘허프만 코드’와 연관이 있다.

그런데 마침 키 값이 가장 작은 노드를 얻어 내는 좋은 자료구조가 있다.
바로 ‘힙(Heap)’이다.

힙을 어떻게 사용하는지는 아래 그림을 통해 설명하였다. 또한 디코딩 방법까지 나타내었으니 참고하길 바란다.

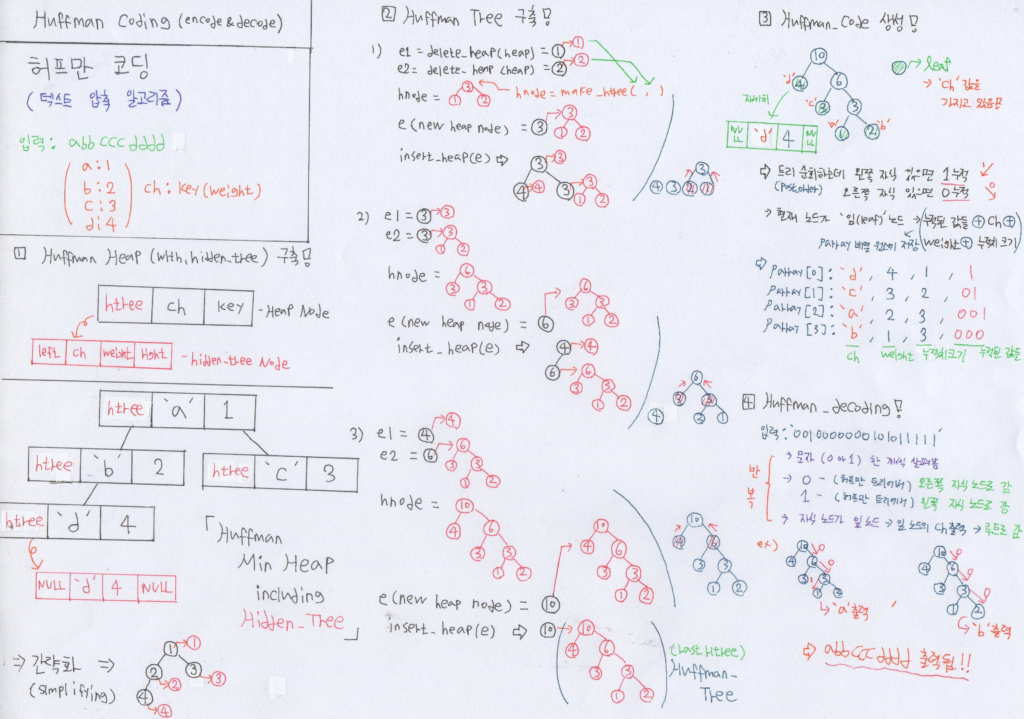
아래에 힙을 이용한 허프만 부호화 (텍스트 데이터 압축)를 C언어로 구현해보았다.

#include <stdio.h>
#include <stdlib.h>
#define MAX 99999

typedef struct TreeNode {
	char ch; // 문자 
	int weight; // 문자의 빈도수(누적치)
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;
typedef TreeNode* TreeNode_ptr;

typedef struct {
	TreeNode_ptr htree; // 히든 트리 
	char ch; // 문자 
	int key; // 문자의 빈도수(누적치) 
}element;

typedef struct {
	element heap[MAX];
	int heap_size;
}HeapType;
typedef HeapType* HeapType_ptr;

HeapType_ptr Heap_init() {
	HeapType_ptr h = (HeapType_ptr)malloc(sizeof(HeapType));
	h->heap_size = 0;
	return h;
}

// 현재 요소의 개수가 heap_size인 히프 h에 item을 삽입한다.
// 삽입 함수
void insert_min_heap(HeapType_ptr h, element item) {
	int i;
	i = ++(h->heap_size);
	// 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정
	// 배열로 트리를 구현하니까 부모 노드의 idx는 1 
	while ((i != 1) && (item.key < h->heap[i / 2].key)) {
		h->heap[i] = h->heap[i / 2]; // 부모를 한 칸 내림 
		i /= 2;
	}
	h->heap[i] = item; // 삽입될 위치가 확실해진 다음에 새로운 노드를 삽입 
}

// 삭제 함수 
element delete_min_heap(HeapType_ptr h) {
	int parent, child;
	element item, temp;
	item = h->heap[1]; // 루트 노드 값을 반환하기 위해 item변수로 옮긴다.
	temp = h->heap[(h->heap_size)--]; // 말단 노드 값을 temp변수로 옮기고 힙 사이즈를 1 줄인다. (처음에는 루트에 위치해있다고 생각) 
	parent = 1;
	child = 2; // 루트의 왼쪽 자식부터 비교한다. 
	// 자식이 힙을 벗어나지 않았으면 반복문 진행 
	while (child <= h->heap_size) {
		// 두 자식노드가 있으면 더 작은 자식노드를 찾는다.
		if ((h->heap[parent * 2].key >= 0) && (h->heap[(parent * 2) + 1].key >= 0)) {
			if ((h->heap[parent * 2].key) < (h->heap[(parent * 2) + 1].key))
				child = parent * 2;
			else
				child = (parent * 2) + 1;
		}
		// 말단 노드를 현재 자식의 부모 노드의 위치에 있다고 생각했을 때, 값이 작거나 같으면 힙 조정할 필요가 X
		if (temp.key <= h->heap[child].key)
			break;
		// 부모 노드 자리에 자식 노드의 키 값을 저장 
		h->heap[parent] = h->heap[child];
		// 한 단계 아래로 이동
		parent = child;
		child *= 2;
	}
	// 말단 노드를 현재 자식의 부모 노드의 위치에 있다고 생각했을 때, 자식 값이랑 작거나 같음 -> 실제로 부모 노드에 저장 
	// (Or) child>h->heap_size로, 위치해야 될 노드에 저장 
	h->heap[parent] = temp;
	return item;
}

// 히든 트리 생성 함수 
TreeNode_ptr make_Htree(TreeNode_ptr left, TreeNode_ptr right) {
	TreeNode_ptr node = (TreeNode_ptr)malloc(sizeof(TreeNode));
	node->left = left;
	node->right = right;
	return node;
}

// 잎 노드 판단 함수 
int is_leaf(TreeNode_ptr T) {
	// 1 1 -> 0
	// 1 0 -> 0
	// 0 1 -> 0
	// 0 0 -> 1 
	return !(T->left) && !(T->right);
}

typedef struct {
	char ch;
	int freq;
	int* codes;
	int codes_stop;
}PrintArray;
PrintArray* parray;

// 허프만 코드가 담긴 배열을 parray 구조체에 저장 
void print_codes_array(int codes[], int stop, int freq, char ch) {
	static int i = 0;
	printf("[%d] %c(freq:%d,stop:%d):", i, ch, freq, stop);
	for (int j = 0; j < stop; j++)
		printf("%d", codes[j]);
	printf("\n");

	parray[i].ch = ch;
	parray[i].freq = freq;
	parray[i].codes_stop = stop;

	for (int k = 0; k < parray[i].codes_stop; k++)
		(parray[i].codes)[k] = codes[k];
	i++;
}

// 허프만 코드가 담긴 배열 생성 
void make_codes_array(TreeNode_ptr T, int codes[], int idx) {
	// 왼쪽 자식이 있으면 1 저장, 순환 호출 
	if (T->left) {
		codes[idx] = 1;
		make_codes_array(T->left, codes, idx + 1);
	}
	// 오른쪽 자식이 있으면 0 저장, 순환 호출
	if (T->right) {
		codes[idx] = 0;
		make_codes_array(T->right, codes, idx + 1);
	}
	// 리프 노드면 허프만 코드 배열을 구조체에 저장 
	if (is_leaf(T)) {
		print_codes_array(codes, idx, T->weight, T->ch);
	}
}

// 허프만 힙을 이용한 허프만 트리 생성 

// 허프만 힙: 허프만 트리 구축을 위한 힙 
// 히든 트리: 허프만 힙의 원소(element)가 갖는 숨겨진 트리 
// 허프만 트리: 허프만 코드 생성울 위한 트리 (최종 히든 트리)

TreeNode_ptr huffman_tree; // 허프만 트리 
void make_huffman_heap(int freq[], char ch_list[], int n) {
	int i;
	TreeNode_ptr hnode; // 히든 트리 노드
	HeapType_ptr h; // 힙 
	element e, e1, e2; // e: 새로 삽입할 힙 원소, e1,e2: 임의 힙 노드  
	int codes[100];

	h = Heap_init();
	// 허프만 힙 초기 세팅 
	for (i = 0; i < n; i++) {
		hnode = make_Htree(NULL, NULL); // 히든 트리 노드 생성 
		e.ch = hnode->ch = ch_list[i]; // 필드에 문자 부여 
		e.key = hnode->weight = freq[i]; // 필드에 문자의 빈도수 부여 
		e.htree = hnode; // 필드에 히든 트리의 주소 부여 
		insert_min_heap(h, e);
	}

	// 허프만 트리 구축 
	for (i = 1; i < n; i++) {
		// 최소값을 가지는 두 개의 노드를 삭제
		e1 = delete_min_heap(h);
		e2 = delete_min_heap(h);
		// 두 개의 노드 합쳐서 새 히든 트리 생성 
		hnode = make_Htree(e1.htree, e2.htree);
		// 허프만 힙에 새 원소 삽입 (두 개의 노드 키를 누적)
		e.key = hnode->weight = e1.key + e2.key;
		e.htree = hnode;
		insert_min_heap(h, e);
	}
	e = delete_min_heap(h);
	huffman_tree = e.htree; // 허프만 트리 (최종 히든 트리)

	// 허프만 트리로 코드 생성 (및 출력) 
	make_codes_array(huffman_tree, codes, 0);
}

int geti;
char get_symbol(char string[]) {
	return string[geti++];
}

char* string = NULL;
int input_processing(char* ch_list, int* freq) {
	// 소문자 알파벳 처리 리스트 생성 
	int alphabet = 26;
	char* alphabet_list = (char*)malloc(sizeof(char) * alphabet);
	int* alphabet_freq = (int*)calloc(alphabet, sizeof(int));
	for (int i = 0; i < alphabet; i++)
		alphabet_list[i] = 'a' + i;

	// 문자열 처리 리스트 생성 
	string = (char*)malloc(sizeof(char) * MAX);
	gets(string);

	// 입력된 알파벳 빈도수 저장 
	char tmp = 0;
	int idx = 0;
	geti = 0;
	while ((tmp = get_symbol(string)) != 0) {
		if ('a' <= tmp && tmp <= 'z') {
			idx = tmp - 'a';
			alphabet_freq[idx]++;
		}
	}

	// 빈도수가 0인 알파벳은 제외 
	int num = 0;
	for (int i = 0; i < alphabet; i++) {
		if (alphabet_freq[i] > 0) {
			ch_list[num] = alphabet_list[i];
			freq[num++] = alphabet_freq[i];
		}
	}

	// 배열 출력
	for (int i = 0; i < num; i++) {
		printf("%c:%d\n", ch_list[i], freq[i]);
	}

	return num;
}

int main(void) {
	// 영어(소문자) 처리 허프만 암호화 

	// 입력한 문자 배열 
	char* ch_list = (char*)malloc(sizeof(char)*MAX);
	// 입력한 문자의 빈도 수 배열
	int* freq = (int*)malloc(sizeof(int)*MAX);
	// 입력받아서 배열에 저장, 문자의 개수 반환 
	int num = input_processing(ch_list, freq);

	// 출력을 위한 구조체 배열 생성 
	parray = (PrintArray*)malloc(sizeof(PrintArray)* MAX);
	for (int i = 0; i < num; i++) {
		parray[i].codes = (int*)malloc(sizeof(PrintArray) * MAX);
	}

	// 알파벳에 따른 호프만 코드들을 구조체에 저장 
	make_huffman_heap(freq, ch_list, num);
	
	// 호프만 코드들을 입력한 문자에 맞게 저장하기 
	int tmp;
	geti = 0;
	char* huffman_encode=(char*)malloc(sizeof(char));
	int huffman_encode_size = 0;
	while ((tmp = get_symbol(string)) != 0) {
		for (int i = 0; i < num; i++) {
			if (parray[i].ch == tmp) {
				for (int k = 0; k < parray[i].codes_stop; k++) {
					huffman_encode[huffman_encode_size++] = (parray[i].codes)[k];
					realloc(huffman_encode, sizeof(char)+huffman_encode_size);
				}
				break;
			}
		}
	}
	
	// 호프만 인코드 결과 보기 
	printf("\n");
	for (int i = 0; i < huffman_encode_size; i++)
		printf("%d", huffman_encode[i]);
	printf("\n");

	// 허프만 트리 이용해서 디코딩하기 
	TreeNode* temp=huffman_tree;
	for (int i = 0; i < huffman_encode_size; i++) {
		if (huffman_encode[i] == 1) {
			temp = temp->left;
			if ((temp->left == NULL) && (temp->right == NULL)) {
				printf("%c",temp->ch);
				temp = huffman_tree;
			}
		}
		else {
			temp = temp->right;
			if ((temp->left == NULL) && (temp->right == NULL)) {
				printf("%c", temp->ch);
				temp = huffman_tree;
			}
		}
	}
	printf("\n");
	
	return 0;
}