분류 알고리즘으로 성능이 우수한 Support Vector Machine을 소개하겠습니다.

SVM 모델은 Decision Boundary(결정 경계)의 여백이 클수록 일반화 능력이 더 좋습니다.
여기서 여백이란 경계와 샘플 간의 거리입니다.

즉 위 그림에서는 _{(여백이 적은)}2번보다 _{(여백이 큰)}3번 경계가 분류하기에 더 적합합니다.

2번 경계와 3번 경계 사이에 새로운 레코드(세모)가 위치했다고 생각해봅시다.
이 세모는 동그라미랑 좀 더 가깝다보니 동그라미로 분류되는 것이 적합할 것입니다.

만일 3번 경계로 분류하면 세모는 동그라미로 분류되겠지만,
2번 경계로 분류하면 세모는 네모로 분류가 됩니다.

즉 우리는 3번과 같은 경계를 만들기 위해 SVM을 배울 필요성이 있습니다.

이제 이 여백에 대해서 더 자세하게 알아 보겠습니다.

여백이라는 개념을 공식화하는 방법을 알아보고,
여백을 최대로 하는 결정 경계를 찾는 방법을 알아볼 것입니다.

그러기 전에 이진 분류와 관련된 수학적 개념부터 알아 봅시다!

0. 경계의 일반화 식은 [ w^tx+b=0 ]입니다.
w^tx에서 w는 [w₁,w₂,w₃,..,w_n]이고 x는 [x₁,x₂,x₃,…,x_n]이라고 생각하면 됩니다.

만약 n이 2이면 직선이고 3이면 평면, 4이상이면 초평면의 경계를 나타냅니다.

쉽게 풀어쓰면 아래와 같습니다.

우리가 알고 있는 일반적인 평면의 식이 ax+by+cz+d=0이라면
이를 [ w₁x₁+w₂x₂+w₃x₃+b=0 ]로 표현한 것입니다.

경계의 일반화 식은 feature가 n개이다 보니 [ w₁x₁+w₂x₂+w₃x₃+…+w_nx_n+b=0 ]로 표현되고
이를 짧게 [ w^tx+b=0 ]로 나타낸 것입니다!

3. 우리가 알고 있는 일반적인 평면에서 법선벡터(Normal Vector)는 (a,b,c)입니다.
즉 [w₁,w₂,w₃]와 같습니다.
따라서 일반화한 경계의 법선벡터는 w[w₁,w₂,w₃,..,w_n]가 됩니다.

4. 우리가 알고 있는 점과 평면 사이의 거리는 아래 이미지와 같습니다.

즉 임의의 점 x[x₁’,x₂’,x₃’]와 평면(w₁x₁+w₂x₂+w₃x₃+b=0) 사이의 거리(d)는
->  | w₁x₁’+w₂x₂’+w₃x₃’+b | / sqrt(w₁²+ w₂²+ w₃²) 입니다.

따라서 일반화한 경계와 임의의 점 x의 거리(h)는 [ |d(x)| / ||w|| ]가 됩니다.
||w|| 에서 이중 막대는 벡터의 크기 의미이며,
|d(x)|가 말하는 것은 | w^tx+b | 식으로 임의의 점x가 같은 경계 위에 놓일 때만 0이 됩니다.

w=(2,1)^T, b=-4라고 생각하고 아래 문제를 풀어 봅시다.

[ d(x): 2x₁+x₂-4=0 ] 과 (2,4)의 거리를 구하는 것입니다.
이를 [ |d(x)| / ||w|| ] 공식에 대입하면 다음과 같습니다.

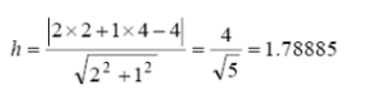
사실 이 문제는 오래 전부터 우리가 알고 있는 문제입니다.

‘[ 직선: y=-2x+4 ]와 점(2,4) 사이의 거리를 구하시오. ‘ 와 같은 문제이기 때문입니다.

즉 문제의 형태가 어려워 보이더라도 쉽게 생각하면 다 아는 내용들을 소개한 것입니다.

여백과 서포트 벡터의 정의

여백(Margin)은 직선에서 가장 가까운 ‘샘플(x)’까지의 거리에 2배를 한 것으로 2h가 됩니다.
서포트 벡터는 직선에서 가장 가까운 ‘샘플(x)’를 의미합니다. 이진 분류에서는 최소 2개의 서포트 벡터가 필요합니다.

즉 여백을 공식화하면 위와 같습니다. | d(x) |가 1이 돼야 하는 이유는 식을 단순화하기 위함입니다.
그리고 여백을 구할 때의 x가 바로 서포트 벡터입니다.

조건부 최적화 문제

여백의 공식에 의하면 직선과 샘플(x)로 구한 | d(x) |는 항상 1이상입니다.

| d(x) |가 1이 될 때는 x가 서포트 벡터이면서 적당한 상수c가 곱해진 경우입니다.

만일 x가 서포트 벡터가 아니면서 적당한 상수c가 곱해졌다면 | d(x) | > 1이 됩니다.
왜냐하면 x가 서포트 벡터보다 직선으로부터 더 멀어지니 h가 커지는데, w는 고정이므로 분자가 커지기 때문입니다.

조건부 최적화 문제는 이렇습니다.

| d(x) | >= 1이면서 경계선의 윗 부분을 ɯ₁(동그라미), 밑 부분을 ɯ₂(네모)라고 분류할 것이다.
이 조건을 만족하면서 여백(2/||w||)을 최대화하는 w벡터를 찾아라!

이 문제를 그림으로 다시 설명하겠습니다.

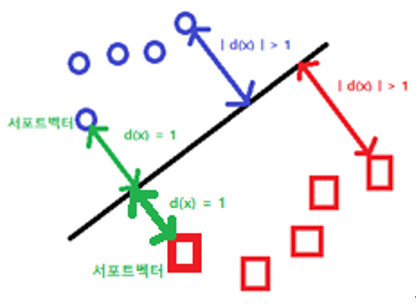
위와 같은 그림을 만족하면서

여백이 가장 큰 w벡터를 찾아라.

그런데 우리한테 좀 더 와닿는 최적화는 Loss Function을 최소화하는 문제입니다.
따라서 최소화 문제로 형태를 바꿔 보겠습니다.

h를 최대화 하라는 것은 1/h을 최소화하라는 것과 같습니다.
또한 1/h = ||w|| / 2인데, ||w||은 루트를 포함한 식이므로 제곱해서 최적화 문제를 더 쉽게 만들었습니다.

이렇게 만들어진 문제의 특성은 다음과 같습니다.

경사하강법(경사도를 이용하여 손실함수의 최솟값을 찾는 방법)을 통해서 최적화를 진행하면, 지역 최적점(Local minimum) 혹은 전역 최적점(Global minimum)을 만나게 됩니다.

Loss Function(손실 함수)에서 최솟값은 아니지만 극솟값인 지점을 Local minimum(Local optimum)이라고 합니다.
Loss Function(손실 함수)에서 최솟값이면서 극솟값인 지점을 Global minimum(Global optimum)이라고 합니다.

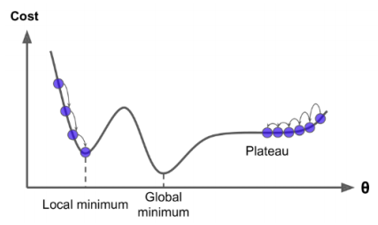
문제의 특성에서 전역 최적점(Global Optimum)을 보장한다는 의미는 초기 값을 어디로 선정하든 Global Optimum을 만나게 된다는 것입니다.

이유는 간단합니다.

J(w)의 식이 Convex(아래로 볼록한 2차 함수 형태)하므로 초기 점을 어디로 선정하든 경사하강법을 진행하면 극솟값이 최솟값이 됩니다.

위처럼 최소화 문제로 변환해 봤지만 부등식 문제가 있어서 여전히 풀기가 난해합니다.

다행히 Convex 성질을 이용하여 풀기 쉬운 형태로 변환하는 Wolfe 듀얼 방법이 있습니다.
따라서 마지막으로 최적화 문제를 더 쉬운 형태로 변환하겠습니다.

아래처럼 변환하면 부등식 조건이 등식 조건이 되어 풀기에 더 유리합니다.

이제 본격적으로 라그랑제 승수법을 이용해서 문제를 풀어 보겠습니다.

J(w)식과 조건식으로 라그랑제 함수 식을 만들고 KKT조건을 이용해서 함수를 풀면 라그랑제 승수(α = λ)를 얻을 수 있습니다. 이 α를 이용하면 w도 구할 수 있습니다.

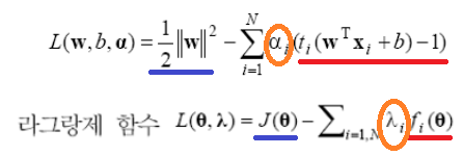
(1) dL/dw = 0 : 라그랑제 함수를 w로 편미분하면 0이 됩니다. (세타는 w)
(2) 라그랑제 승수는 0보다 크거나 같습니다.
(3) 라그랑제 승수와 조건 식과 곱한 값은 0입니다.

라그랑제 함수를 KKT조건에 적용하면 아래와 같습니다.

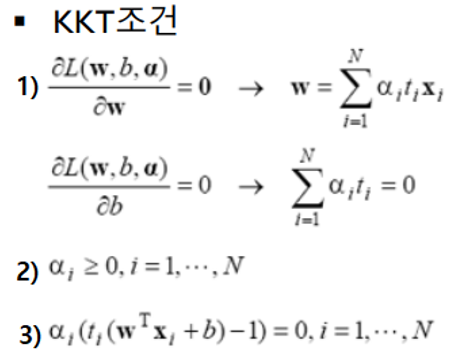
(3)에 의하면 모든 샘플이 α_i = 0 또는 t_i(w^Tx_i+b)-1=0이어야 됩니다.
w^Tx_i+b = 1는 d(x)=1과 같고 여백의 공식에 의하면 x는 서포트 벡터이기 때문에
α_i != 0일 때(t_i(w^Tx_i+b)-1=0일 때) 샘플이 서포트 벡터가 됩니다.
즉 0이 아닌 α를 구하면 됩니다.

(1)에 의하면 α를 통해 w를 구할 수 있습니다. (t와 x(샘플)의 값은 주어짐)
x가 서포트 벡터일 때 구한 w는 여백을 최대로 만드는 w입니다.
다시 (3)에 의하면 α와 w로 b값을 수할 수 있습니다!

위에 써진 KKT조건 (1-1)과 (1-2)를 라그랑제 함수에 대입하여 정리하겠습니다. (증명 생략)
N은 샘플의 개수입니다.

이제 라그랑제 함수가 정리가 됐고 α,w,b 구하는 방법도 알게 되었습니다.

아래 예제를 통해 [여백을 최대화하는 w벡터]와 [d(x):결정 경계]를 찾아 보겠습니다!

예제1) 두 개의 샘플을 가진 경우의 문제 풀이

훈련집합 x₁=(2,3)^T, t₁=1
훈련집합 x₂=(4,1)^T, t₂=-1

α를알았으니 KKT조건 (1)에대입해서 w를구합니다.
다시 KKT조건(3)에대입해서 b를 구합니다.

예제2) 세개의샘플을가진경우의문제풀이

훈련집합 x₁=(2,3)^T, t₁=1
훈련집합 x₂=(4,1)^T, t₂=-1
훈련집합 x₃=(5,1)^T, t₃=-1

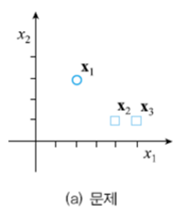
위 집합을 라그랑제 함수에 대입하면 아래와 같습니다.

α_i != 0일 때 샘플이 서포트벡터입니다.
α가 여러 개이기 때문에 경우를 나누어서 분석적으로 풀이를 해야 합니다!

그런데 왜 0이 2개 이상인 경우는 없을까요? (ex) a₁=0, a₂=0, a₃!=0)
Classification을 하기 위해서는 서포트 벡터는 2개 이상이어야 되기 때문입니다.

분석해본 결과 (3)번의 풀이법이 적합하였습니다.
나머지 풀이법이 왜 안 되는지는 마지막에 설명하겠습니다.

α를알았으니 KKT조건 (1)에대입해서 w를구합니다.
다시 KKT조건(3)에대입해서 b를 구합니다.

나머지 풀이법이 안 되는 이유

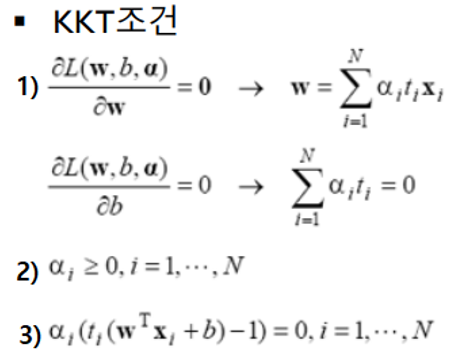
①: α2+α3=0을 성립하는 α2와 α3는 0밖에 없습니다. 서포트 벡터는 2개 이상이 되어야 하기 때문에 틀립니다.

②: α1=α3이 됩니다.
L에다 대입 시 -> L(α₁)=2α₁-13/2α₁² 이 나오고 이 식을 미분하면 α₁은 2/13이 되고 α₃도 마찬가지입니다.
α를 알았으니 KKT조건 (1)에 대입해서 w를 구합니다. 다시 KKT조건(3)에 대입해서 b를 구합니다.
-> w=(-613,4/13), b=1 이 나옵니다.
d(x)=w^Tx+b이고 w,x,b가 다 구해졌으니 d(x₁),d(x₂),d(x₃)를 구해보면
d(x₁)=1, d(x₂)=-7/13, d(x₃)=-1이 나옵니다.
그런데 t_i * d(x_i) >= 1은 무조건 만족해야 됩니다.
α2=0이니까 이 때 x2는 서포트 벡터가 아니어야 하므로 t₂ * d(x₂) > 1이어야만 합니다.
그러나 t₂ * d(x₂) = 7/13이 되므로 모순입니다.

④: α₁=α₂+α₃가 됩니다.
L에다 대입 후 최대값을 구하기 위해 α₂와 α₃에 대해서 각각 편미분을 합니다.
dL/dα₂ = dL/dα₃ = 0을 구합니다.
그 결과 α₂=3/2, α₃=-1이 나오는데 α₃가 KKT조건(2)에 위배되므로 모순입니다.

선형 분리가 가능한 상황과 선형 분리가 불가능한 상황

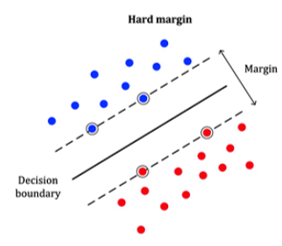
선형 분리가 가능한 상황입니다.
t(w^Tx+b) >= 1을 만족합니다.

선형 분리가 불가능한 상황입니다.
분할은 됐으나 분할 띠 안 쪽에 데이터가 있습니다.
0 <= t(w^Tx+b) < 1에 해당합니다.

선형 분리가 불가능한 상황입니다.
잘못 분류한 데이터가 있습니다.
t(w^Tx+b) < 0에 해당합니다. <오분류 발생>

이러한 세 가지 경우를 나타내는 변수가 있습니다.
바로 슬랙변수(Slack)입니다.

또한 성능을 높이기 위한 새로운 문제를 직면하게 됩니다.

여백을 최대한 크게 하면서 (경우2)와 (경우3)을 최대한 적게 하는 w를 찾아라
목적1) 여백을 될 수 있는 한 크게 하기
목적2) 경우2와 경우3을 최대한 적게 하기

이 문제를 풀기 위한 새로운 목적 함수를 제시합니다.

C를 크게 하면 ||w||에 덜 신경쓰고 오차에 더 집중합니다. 커진 C를 곱함으로써 오차가 더 돋보이기 때문입니다.
이러면 ||w||가 커져서 ‘여백’이 줄어드는 모습을 보입니다.
-> 띠 안쪽에 있는 샘플 수는 줄어들지만(+) 일반화 능력이 떨어지는(-) 방법

C를 작게 하면 오차를 덜 신경쓰고 ||w||에 더 집중합니다. 따라서 ‘여백’은 늘어나는 모습을 보입니다.
-> 일반화 능력은 높아지지만(+) 띠 안쪽에 오는 샘플 수가 늘어나는(-) 방법

즉 위의 C를 잘 조정해서 문제를 풀어야 될 것입니다!

비선형 SVM

데이터가 위와 같이 분포되어 있으면 선형 SVM으로 분류할수가 없습니다.

이럴 때 사용하는 분류 기법이 비선형 SVM입니다.

비선형 SVM은 선형 경계 대신 면형 경계를 이용합니다.

즉 차원을 바꾼 후 면형 경계를 사용해서 분류하는 방식입니다!

위처럼 차원을 바꾸는 것을 공간 맵핑이라고 합니다.
공간 맵핑을 해주는 함수는 맵핑 함수라고 합니다.

SVM은 ‘맵핑 함수’와 비슷한 기능을 하는 ‘커널 함수’를 사용합니다!
이 커널 함수는 ‘다항식 커널’과 ‘RBF‘중 선택해서 사용할 수 있습니다.

결국 커널 함수를 이용해서 차원을 바꾸고, 클래스를 나누는 Decision Boundary를 구하면 끝입니다!

from preamble import *
from sklearn.datasets import make_blobs
from sklearn.svm import LinearSVC

X,y=make_blobs(centers=4,random_state=8)
y=y%2

mglearn.discrete_scatter(X[:,0],X[:,1],y) # feature0, feature1 이용해서 데이터를 위치 시킴, y는 클래스 
plt.xlabel("feature 0")
plt.ylabel("feature 1")
plt.legend(["class 0","class 1"])

linear_svm=LinearSVC().fit(X,y)

mglearn.plots.plot_2d_separator(linear_svm,X)
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel("feature 0")
plt.ylabel("feature 1")

from mpl_toolkits.mplot3d import Axes3D, axes3d

# 두 번째 특성을 제곱하여 추가합니다
X_new=np.hstack([X,X[:,1:]**2]) # 새로운 차원에 feature1인 데이터를 올려 놓음 
figure=plt.figure()

# 3차원 그래프
ax=Axes3D(figure,elev=-150,azim=30)

# y==0인 포인트를 먼저 그리고 그 다음 y==1인 포인트를 그립니다.
mask=y==0
ax.scatter(X_new[mask,0], X_new[mask,1], X_new[mask,2], c='b', edgecolor='k') #y=0인거 그리기 
ax.scatter(X_new[~mask,0], X_new[~mask,1], X_new[~mask,2], c='r', edgecolor='k',marker='^') #y가 1인거 그리기 
ax.set_xlabel("feature 1")
ax.set_ylabel("feature 2")
ax.set_zlabel("feature 1 ** 2")
plt.show()

linear_svm_3d=LinearSVC().fit(X_new,y)
coef=linear_svm_3d.coef_.ravel()
intercept=linear_svm_3d.intercept_

# 선형 결정 경계 그리기
figure=plt.figure()
ax=Axes3D(figure, elev=-150,azim=-30)
xx=np.linspace(X_new[:,0].min()-2, X_new[:,0].max()+2,50)
yy=np.linspace(X_new[:,0].min()-2, X_new[:,0].max()+2,50)


XX, YY = np.meshgrid(xx,yy)
ZZ=(coef[0]*XX+coef[1]*YY+intercept) / -coef[2] # ax+by+cz+d=0 (a,b,c):coef, d:intercept 
ax.plot_surface(XX,YY,ZZ,rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask,0], X_new[mask,1], X_new[mask,2], c='b', edgecolor='k') #y=0인거 그리기 
ax.scatter(X_new[~mask,0], X_new[~mask,1], X_new[~mask,2], c='r', edgecolor='k',marker='^') #y가 1인거 그리기 
ax.set_xlabel("feature 1")
ax.set_ylabel("feature 2")
ax.set_zlabel("feature 1 ** 2")

지금까지 SVM 이론을 알아 보았습니다.

감사합니다!