클러스터링(군집화)는 클래스 정보(타깃 정보)없이 데이터를 나누는 작업을 의미합니다.
비지도학습으로 정답이 없기 때문에, 주관적인 판단에 따라 결과가 달라지는 특징이 있습니다!
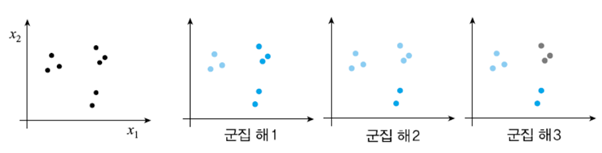
데이터를 나눌 때는 유사도를 이용합니다.
유사도는 보통 거리를 이용해서 구합니다!
아래는 레코드 간의 거리를 구할 때 쓰이는 방법입니다.

위 예시에서 해밍 거리는 3이 됩니다. 해밍 거리가 가까울수록, 즉 값이 작을수록 데이터는 유사합니다.
Cosine유사도 같은 경우, 세타가 작을수록(코사인 값이 클수록) 데이터는 유사합니다.
이번에는 레코드와 군집 사이의 거리에 대해 알아 보겠습니다.


Dmax는 점과 군집의 가장 먼 점과의 거리를 구하는 방식입니다.
Dmin는 점과 군집의 가장 가까운 점과의 거리를 구하는 방식입니다.
Dave는 점과 군집에 있는 점들 사이의 거리들의 평균을 구하는 방식입니다.
Dmean은 점과 군집의 평균점 사이의 거리를 구하는 방식입니다.
Drep은 (군집 내에서 다른 점과의 거리의 합이 가장 작은 점)과 점 사이의 거리를 구하는 방식입니다.
아래는 점과 군집 사이의 거리 예시입니다.

위의 방식들 중에서는, 무난하고 극단값에 영향을 덜 받는 Dave가 가장 많이 사용됩니다!
이제 클러스터링의 핵심인 K-means 알고리즘에 대해 알아 보겠습니다!
k는 군집의 개수이고, 아래는 k가 3일 때의 예시입니다.
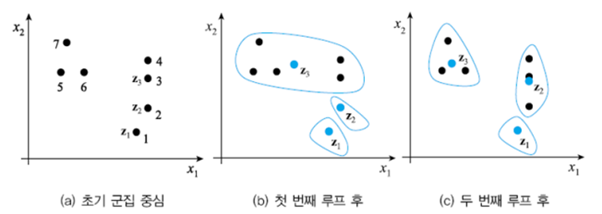
K-means알고리즘은 아래와 같은 구성을 지닙니다.
[ 랜덤으로 센터 지정 -> (거리 공식으로 그룹 (재)지정 -> 평균값으로 센터 지정) 반복 -> 재 지정을 해도 크게 차이가 없는 경우가 생김 -> 종료 ]
1. 랜덤에 의해 [ z1=1, z2=2,z3=3 ] 으로 센터들이 지정됩니다.
2. 센터와 가까운 아이템들로 그룹을 지정합니다. (1),(2),(3~7) <아이템: 센터를 제외한 레코드 / 거리 공식 이용>
3. 평균값으로 센터를 재 지정합니다. (z3이 두 번째 그림과 같이 변경 됨)
– 1차 루프 끝-
4. 변경된 센터와 가까운 아이템들로 그룹을 재 지정합니다. (1),(2,3,4),(5,6,7,z3)
5. 평균값으로 센터를 재 지정합니다. (z2와 z3이 세 번째 그림과 같이 변경 됨)
– 2차 루프 끝-
6. 변경된 센터와 가까운 아이템들로 그룹을 재 지정했는데 큰 변화가 없습니다.
즉 그룹을 재 지정하고 센터를 구했는데 센터가 같습니다. -> 프로그램 종료
결론: (1),(2,3,4),(5,6,7)
다음은 K-means알고리즘의 특징입니다.
- 초기점(랜덤 센터)에 따라 클러스터의 결과가 달라질 수 있다.
- 항상 지역 최적점으로 수렴한다. 전역 최적점을 보장하지 않는다.
(최적화를 할 때 항상 최선의 최적화를 하지 못 한다. 이를 극복하려면 다중 초기점을 사용해야 한다.) - 극단값에 민감하다. (극단값인 점 하나만 그룹이 되는 경우가 발생한다.)

4. 중심을 선정한 다음 거리 공식을 이용하다보니 잘못된 군집화가 일어날 수 있다.
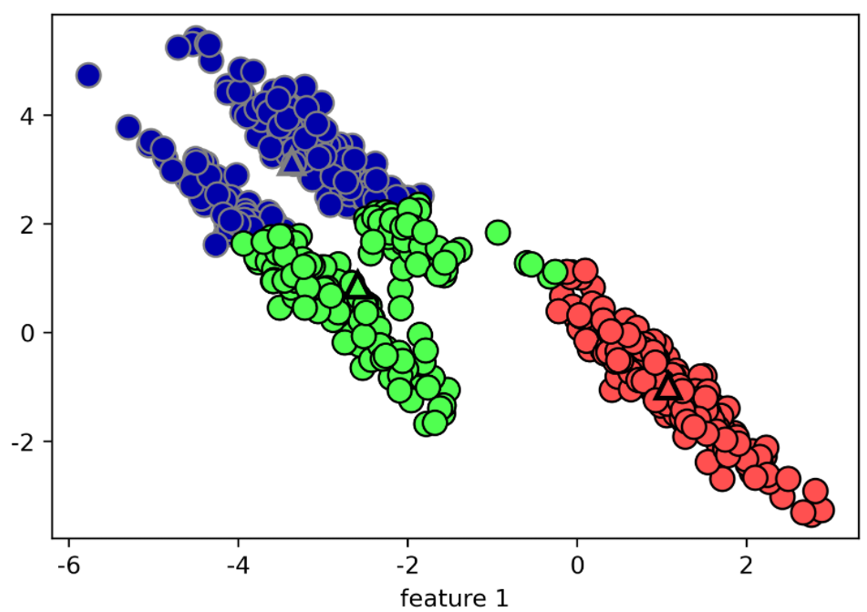
특징으로만 보면 k-means의 한계는 분명해보이고 이를 극복할 알고리즘도 필요해 보입니다.
다행히 밀도 기반 군집화(DBSCAN)이라는 방법이 존재합니다.
이번에는 이 방법에 대해 소개하겠습니다.
밀도 기반 군집화 (DBSCAN)
DBSCAN은 클러스터의 개수를 미리 지정할 필요가 없습니다.
붐비는 지역(Dense Region)인지 검색하고 군집화를 하는 방법입니다.
좀 더 자세히 알기 위해 DBSCAN에 관련된 여러 용어를 알아 봅시다.
포인트는 데이터 포인트, 즉 샘플(레코드) 입니다.
잡음 포인트(noise)는 어떠한 클래스에도 속하지 않는 포인트를 의미합니다.
Eps는 사용자로부터 설정되는 거리를 의미합니다. 엡실론(epsilon)으로 불립니다.
min_samples는 Dense Region의 기준이 되는 샘플의 개수입니다. (사용자로부터 설정됨)
Dense Region은 eps거리 안에 있는 포인트 수가 min_samples보다 컸을 때, 해당 지역은 Dense Region입니다.
핵심 샘플은 Dense Region에 속하는 샘플(포인트,레코드)입니다.
DBSCAN의 알고리즘은 아래와 같은 구성을 지닙니다.
[ 무작위로 포인트 선택 -> 포인트에서 Eps거리 안의 모든 포인트를 살펴봄 -> Eps 안에 있는 포인트 수가 min_samples보다 적으면 해당 지역의 포인트들을 noise로 레이블링 / Eps안에 있는 포인트 수가 min_samples보다 많다면 해당 지역은 Dense Region, 선택된 포인트를 핵심 샘플로 지정하고 새 클러스터를 생성 -> Dense Region에 위치한 모든 포인트들을 클러스터로 레이블링 ]
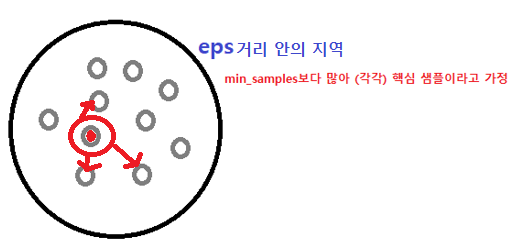
내부가 빨간 포인트가 무작위의 포인트라고 생각합시다.
포인트들을 감싸는 검은색 원이 eps거리 안의 지역(영역)이라고 생각합시다.
eps안에 있는 포인트 수는 min_samples보다 많아서, 내부 포인트들이 핵심 샘플이라고 생각합시다.
eps거리 안의 지역은 Dense Region이기 때문에 클러스터를 생성할 수 있습니다.
그렇게 만들어진 클러스터가 빨간색 원입니다.
이 클러스터는 Dense Region에 있는 모든 핵심 샘플들을 추가해나갑니다.
위의 작업이 무작위로 포인트를 선택한 다음, 클러스터가 만들어지는 과정입니다.
모든 포인트를 다 볼 때까지 알고리즘은 진행됩니다.
이제 DBCAN의 특징을 알아 보겠습니다.

eps가 클수록 ‘eps거리 안의 지역’이 크다는 것이고, 그 안에 있는 샘플들도 많기 때문에 클러스터가 생성된다면 크게 생성됩니다. eps가 너무 크면 모든 포인트들이 한 영역에 속할 수 있고 하나의 클러스터만 만들어질 수 있습니다.
eps가 작을수록 ‘eps거리 안의 지역’이 작다는 것이고, 그 안에 있는 샘플들도 적기 때문에 클러스터가 생성된다면 작게 생성됩니다. eps가 너무 작으면 포인트 수가 min_samples의 수보다 작을 확률이 커지기 때문에 대부분이 noise가 됩니다.
min_samples가 클수록 noise가 늘어납니다. 아무리 영역 안에 있는 포인트가 많아도 min_samples의 수보다 작으면 모두 noise로 레이블링되기 때문입니다.
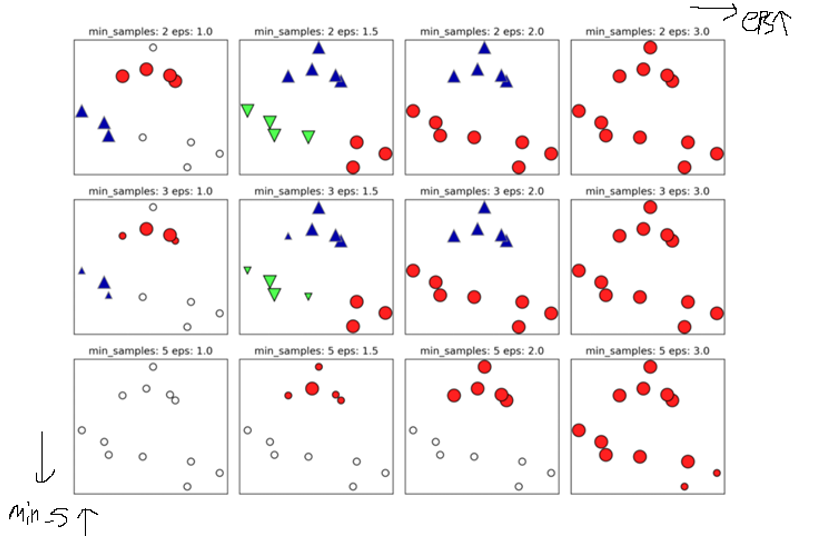
위의 min_samples와 eps를 잘 조정하면 k-means에서 하기 힘든 군집화도 해결이 가능합니다!
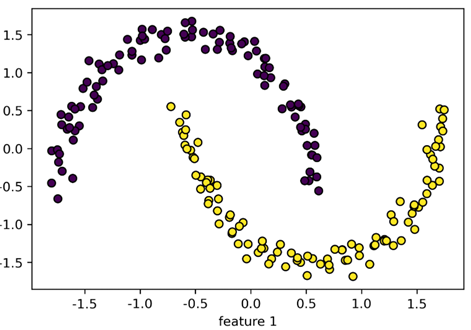
지금까지 클러스터링에 대한 소개였습니다.
감사합니다.
