Decision Tree (의사결정나무)
전체 자료를 몇 개의 소집단으로 분류(classification)하거나 예측(prediction)하는 분석 방법

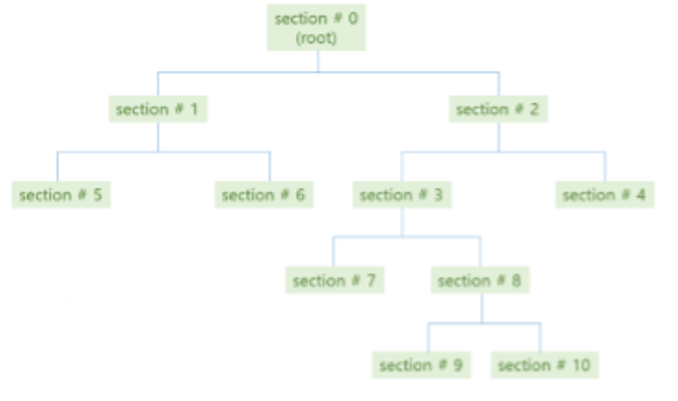
위의 그림과 같은 형태를 결정 트리(DT)라고 합니다.

결정 트리를 만드는 방법을 아래와 같습니다.

레코드가 비슷한 공간끼리 나누기 (->) 나눈 공간은 각각 노드로 지정하기 (->) 노드는 계층 구조로 표현하기

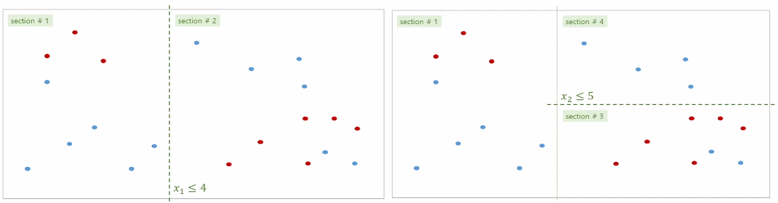
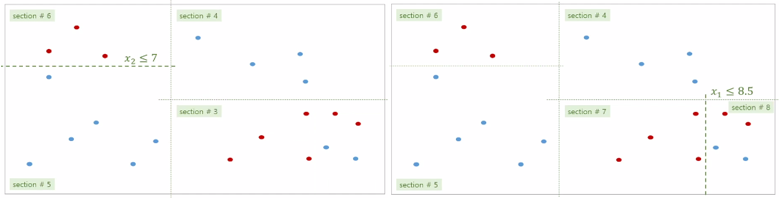
위는 전체 데이터를 8개의 공간(루트 제외)으로 만드는 과정을 나타낸 것입니다.
공간을 만들 때는 비슷한 데이터끼리 나누니 질서있게 분할한다고 말할 수 있습니다.
이를 ‘무질서도(엔트로피)가 적은 쪽’으로 분할한다고 표현합니다.

이러한 결정 트리는 왜 필요한 것일까요?
Iris 결정 트리를 봐보도록 하겠습니다!

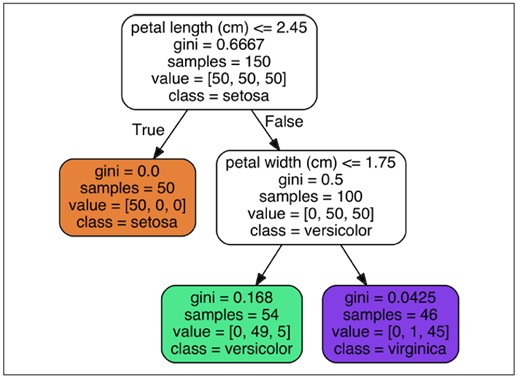
‘꽃잎(petal) 길이(length)가 2.45보다 크거나 같은 구간/ 작은 구간’으로 먼저 분할하였고,
작은 구간은 다시 ‘꽃잎(petal) 너비(width)가 1.75보다 크거나 같은 구간/작은 구간’으로 분할하였습니다.

따라서 구간은 총 세 구간이 됩니다.
각각의 구간에는 붓꽃(iris)의 서로 다른 정보가 들어가 있습니다.

주황색 노드 구간에는 setosa라는 붓꽃의 정보만 모여 있습니다.
초록색 노드 구간에는 vercivolor라는 붓꽃의 정보만 모여 있습니다.
보라색 노드 구간에는 virfinica라는 붓꽃의 정보만 모여 있습니다.

결국 DT를 이용하면 전체 집합을 소집단으로 분류가 가능해집니다!

아래는 이러한 DT의 특징을 정리한 것입니다.

– 트리의 depth가 클수록 많이 나눈 것
– depth가 커질수록 복잡한 모델이 생성됨
– depth가 너무 커지면 오버피팅이 발생할 수 있음
– depth를 적당히 늘려서 정확도가 높은 모델을 생성하면 됨

그런데 과연 어떻게 분할해야 엔트로피가 작아지게 할 수 있을까요?

이제 DT를 생성하는 방법을 더 자세하게 알아 보겠습니다.

DT를 생성하는 것은 곧 구간을 만드는 것이고, 구간을 만드는 것은 질문(Tests)으로 결정합니다.
질문(Tests)에 대해서 Yes인 것들과 No인 것들로 구간을 만드는 방식입니다.
단 질문은 임의로 생성된 것이 아니라 엔트로피 검사를 통해 만들어졌으며, 클래스를 잘 나누는것으로 선정됩니다.

즉 Tests가 DT모델을 만들 때 나누는 기준/경계가 됩니다!
우리는 모든 리프 노드의 엔트로피가 0일 될 때까지 Tests를 생성하고 분할을 계속할 것입니다.

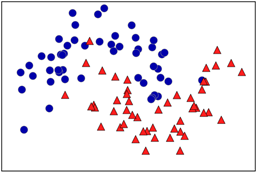
아래의 데이터를 통해 DT를 생성해보겠습니다!
파란 동그라미가 Class0, 빨간 세모가 Class1이라고 가정합니다.

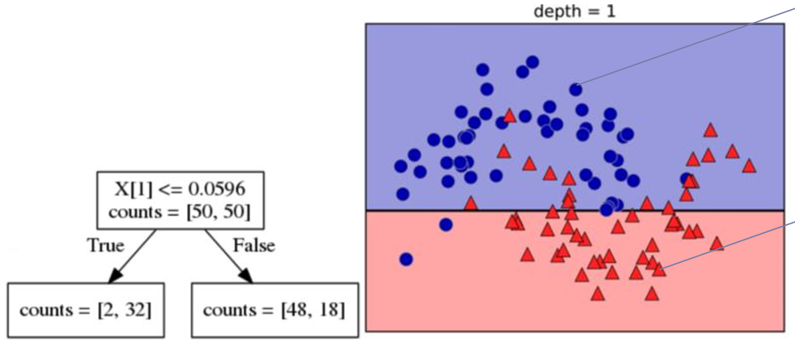
1. X[1]:Y축이 0.0596보다 작거나 같으면 Yes, 크면 No로 분할한다.
-> Yes: Class0이 2개, Class1인 레코드가 32개 <South에 위치>
-> No: Class0이 48개, Class1인 레코드가 18개 <North에 위치>

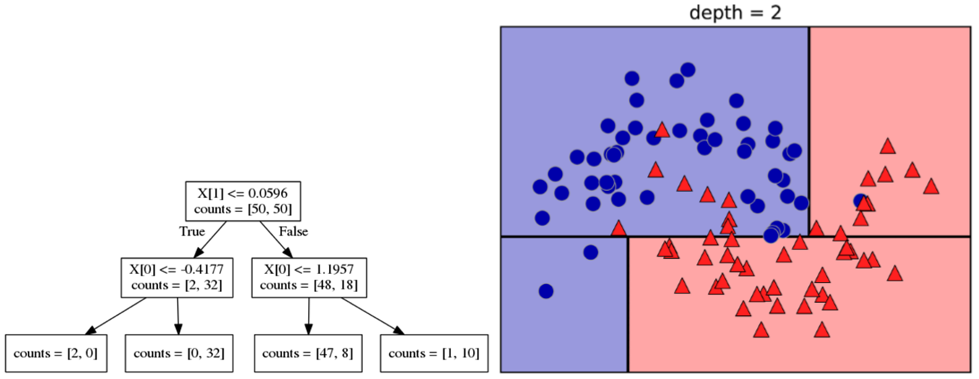
2. X[0]:X축이 -0.4177보다 작거나 같으면 Yes, 크면 No로 분할한다.
-> Yes: Class0이 2개, Class1인 레코드가 0개 <South West에 위치>
-> No: Class0이 0개, Class1인 레코드가 32개 <South East에 위치>

X[0]:X축이 1.1957보다 작거나 같으면 Yes, 크면 No로 분할한다.
-> Yes: Class0이 47개, Class1인 레코드가 8개 <North West에 위치>
-> No: Class0이 1개, Class1인 레코드가 10개 <North East에 위치>

Tests를 추가한 2차 학습 결과,<South West>위치에서 클래스의 수가 0인 경우 발생(엔트로피 0)합니다.
이렇게 되면 해당 서브 트리는 더이상 업데이트 하지 않습니다.
또한 해당 노드는 Pure Node(클래스의 수가 0인 노드)라고 불립니다.

위의 작업을 반복해서 Depth가 7이 되도록 만들어 보았습니다.

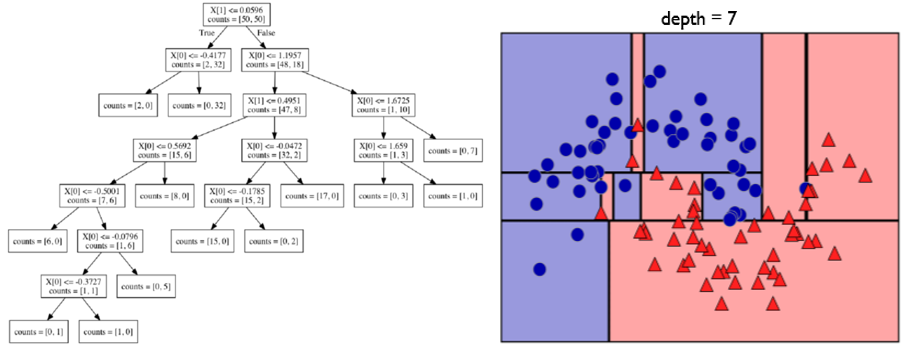
7차 학습을 해서 Depth가 7이 되었고, Pure Node는 최대치가 되었습니다.
즉 모든 리프 노드가 Pure Node가 되었습니다.

이렇게 만들어진 모델은 정확도가 100%를 자랑할 것입니다.
그러나 어느 모델이나 그랬듯 과대적합이 발생할 것입니다.

과대 적합을 줄이는 방법은 두 가지가 있습니다.

위 둘 중에서 많이 사용되는 방법은 사전 가지치기입니다.
max depth를 제한해서 분할을 덜 함으로써 모델을 간단하게 만드는 방법입니다!

결정 트리 분석: 특성 중요도

DT를 분석할 때 우리는 ‘특성 중요도’를 찾을 수 있습니다.

즉 분류를 하기 위해서 어떤 특성(열)이 중요한지 알 수 있다는 것입니다.

이 특성 중요도는 0~1 범위 사이로 나타낼 수 있습니다.
0인 특성은 전혀 사용하지 않는다는 의미이고, 1인 특성은 완벽하게 타깃 클래스를 예측한다는 의미입니다.

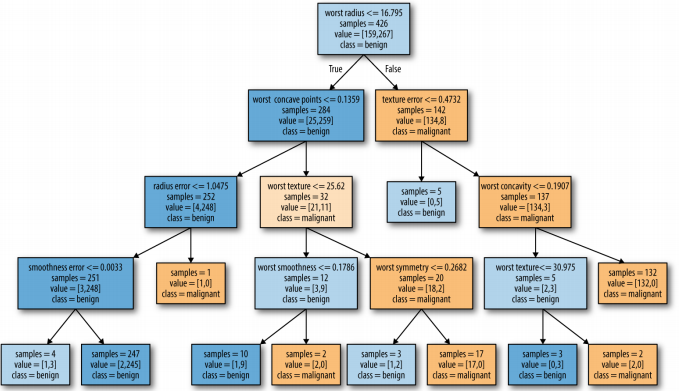
아래 코드를 통해 DT로 유방암 데이터를 분류해보고 특성 중요도를 찾을 수 있습니다.

import warnings
warnings.filterwarnings(action='ignore')
from preamble import *

# 결정 트리의 복잡도 제어하기
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
    cancer.data, cancer.target, stratify=cancer.target, random_state=42)
tree= DecisionTreeClassifier(random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))

# max_depth 수정
tree= DecisionTreeClassifier(max_depth=4,random_state=0)
tree.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(tree.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(tree.score(X_test, y_test)))

# 결정 트리 분석 
from sklearn.tree import export_graphviz
export_graphviz(tree, out_file="tree.dot", class_names=["악성","양성"],
                feature_names=cancer.feature_names, impurity=False, filled=True)
import graphviz

with open("tree.dot", encoding='UTF8')as f:
    dot_graph=f.read()
display(graphviz.Source(dot_graph))


# 트리의 특성 중요도
print("특성 중요도:\n",tree.feature_importances_)

def plot_feature_importances_cancer(model):
    n_features=cancer.data.shape[1]
    plt.barh(np.arange(n_features),model.feature_importances_, align='center')
    plt.yticks(np.arange(n_features),cancer.feature_names)
    plt.xlabel("feature importance")
    plt.ylabel("feature")
    plt.ylim(-1,n_features)
    plt.show()
    
plot_feature_importances_cancer(tree)

코딩 오류 해결법: https://blog.naver.com/PostView.nhn?blogId=ssdyka&logNo=221242275911 (누네띠네님 포스팅)

DT Ensemble (앙상블) – 랜덤 포레스트

DT 앙상블은 DT의 단점을 해결할 수 있는 방법입니다.
즉 Depth가 높을수록 오버피팅이 발생하는 것을 보완하는 방법입니다.

바로 과대적합 트리를 여러 개 만들고 결과를 평균 내어 과대적합을 줄이는 것입니다!

과대적합을 줄이기 위해 과대적합을 이용한다니.. 말도 안 되는 것 같지만 놀랍게도 잘 작동하는 방법입니다.
또한 이는 수학적으로 증명된 내용이라고 합니다!

단 아무렇게나 과대적합 트리를 선정하지는 않습니다.
과대적합이기는 하나 타깃 예측을 잘하는 편이고, 다른 트리와 구별되어야 한다는 조건을 만족해야 합니다.

위 방법을 더 자세하게 알아보기 위해 ‘랜덤 포레스트’를 소개하겠습니다!

랜덤 포레스트는 앙상블 기법 중 배깅에 속하는 방법입니다.

앙상블은 동일하거나 서로 다른 학습 알고리즘을 사용해서 여러 모델을 생성하는 개념으로
여러 모델을 이용하면, 한 가지 모델을 이용하는 것보다 성능이 향상될 것이라는 생각으로 생겨 났습니다!

배깅은 샘플을 여러 번 뽑아(Bootstrap) 각 모델을 생성하고 결과물을 집계(Aggregration)하는 방법입니다.
부트 스트랩(무작위 복원 추출)으로 샘플들을 선정한 후 각 샘플을 이용해서 학습 모델을 만들고 결과를 평균내는 방법입니다.

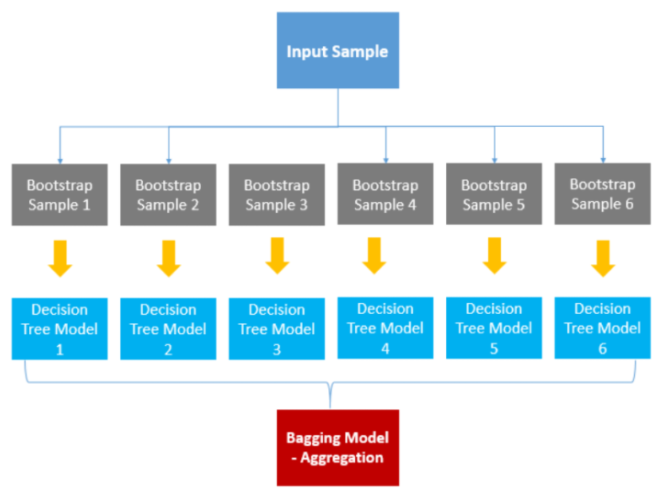
랜덤 포레스트는 DT를 여러 번 이용하는 앙상블 배깅 방법입니다.
그러나 배깅과는 약간의 차이를 지닙니다.

각 샘플이 만든 모델마다 다른 특성(feature)를 사용한다는 점입니다.

예를 들어 배깅은 (나이,성별,수입,거주지)특성을 각 샘플이 모두 가지고 있습니다.
그러나 랜덤 포레스트는 A샘플은 (나이,성별,수입)만 쓰고 B샘플은 (성별,수입,거주지)등을 쓰는 방식으로 샘플마다 데이터의 차이를 보입니다.

아래는 make_moons를 이용해서 랜덤 포레스트 구현을 해보았습니다!

# 앙상블 테스트
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer

# 부트스트랩 테스트
X,y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train,X_test,y_train,y_test=train_test_split(X,y, stratify=y, random_state=42)

forest=RandomForestClassifier(n_estimators=5, random_state=2)
forest.fit(X_train,y_train)

fig, axes=plt.subplots(2,3,figsize=(20,10))
for i, (ax,tree) in enumerate(zip(axes.ravel(), forest.estimators_)):
    ax.set_title("tree {}".format(i))
    mglearn.plots.plot_tree_partition(X,y,tree,ax=ax)
    
mglearn.plots.plot_2d_separator(forest, X, fill=True, ax=axes[-1,-1], alpha=.4)
axes[-1,-1].set_title("random forest")
mglearn.discrete_scatter(X[:,0],X[:,1],y)

print("훈련 세트 정확도: {:.3f}".format(forest.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(forest.score(X_test, y_test)))

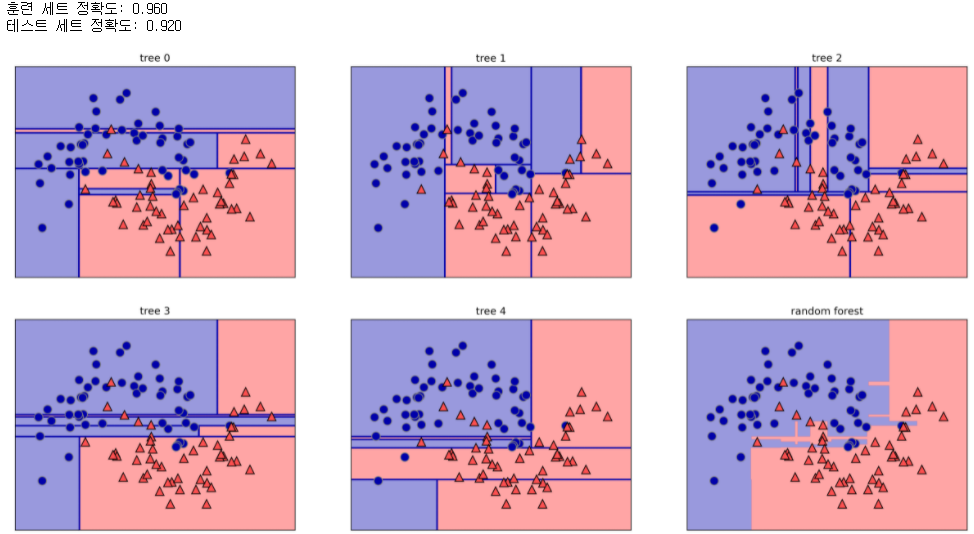
랜덤 트리를 5개만들고 집계해서 만들어진 Random Forest는 96%의 정확도를 보입니다.

DT Ensemble (앙상블) – 그래디언트 부스팅 회귀 트리

랜덤 포레스트가 과대 적합 트리들을 이용해서 성능을 높인 것이라면
그래디언트 부스팅 회귀 트리는 성능이 안 좋은 트리들을 이용해서 성능을 높이는 방법입니다!

개별적인 모델은 성능이 좋지 않지만 모아서 썼더니 성능이 좋아졌다는 것입니다!

각각의 모델은 Weak Learner라고 표현되고 1~5depth정도의 깊지 않은 트리에 해당합니다.

즉 앙상블의 ‘그래디언트 부스팅’ 기법은 weak learner을 많이 연결하여 성능을 높이는 방법입니다.
weak learner가 합쳐지면 더 강력한 모델이 형성됩니다!

아래는 그래디언트 부스팅 회귀 트리 구현을 해보았습니다!
위의 랜덤 포레스트 소스에 이어서 작성하시면 됩니다.

# 부스팅 테스트
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train,y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))

gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train,y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))

gbrt = GradientBoostingClassifier(random_state=0,max_depth=0.01)
gbrt.fit(X_train,y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train,y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))

gbrt = GradientBoostingClassifier(random_state=0,max_depth=1)
gbrt.fit(X_train,y_train)

depth가 최대인 경우, depth가 1인 경우, depth가 0.01인 경우로 나누어 성능을 측정해보았습니다.
아무리 ‘그래디언트 부스팅’이 성능이 안 좋은 WeakLearner을 사용한다고는 하지만 언더피팅인 모델은 처리하지 못 하는 것을 보입니다.

앙상블 추가 개념을 제시하면서 본 포스팅을 마칩니다.

감사합니다.

앙상블 – 추가 개념

보팅과 배깅의 차이 – 다른 학습 알고리즘을 사용하면 보팅, 같은 학습 알고리즘을 사용하면 배깅

패스팅– 배깅과 원리는 같지만, 샘플을 선택할 때 중복을 선택하지 않는 방법

하드 보팅 – 최종 예측치로 투표(집계)하는 방법 <다수결 원칙>

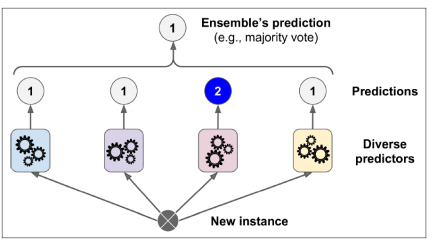
소프트 보팅 – 각 클래스가 될 확률 값을 가지고 투표하는 방법
(ex) 모델1에서 클래스1이 나올 확률:0.8, 클래스2가 나올 확률:0.2 / 모델2에서 클래스1이 나올 확률:0.7, 클래스2가 나올 확률:0.3 / 모델3에서 클래스1이 나올 확률:0.6, 클래스2가 나올 확률:0.4 -> 클래스1 평균> 클래스2 평균이므로 클래스1로 분류)

Ada Boost(아다 부스팅) – 잘 예측하지 못한 레코드에 weight를 줘서 이 레코드를 더 신경써서 classification을 하도록 한다.

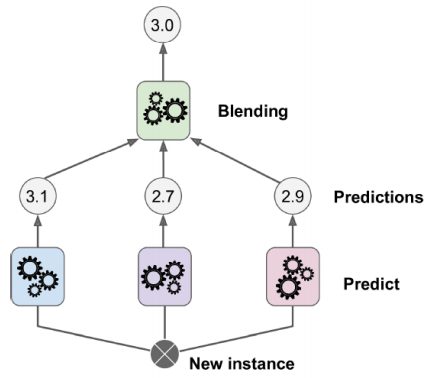
스태킹 – 결과를 다시 입력으로 써서 최종적으로 분류하는 방법, 마지막으로 거치는 분류기를 ‘블렌더’라고 한다.
(ex) 모델1에서 3.1이라고 예측함, 모델2에서 2.7이라고 예측함, 모델3에서 2.9라고 예측함 / 이 세 결과 값을 블렌더에 입력으로 넘김 -> 블렌딩 작업을 함 -> 최종 예측은 3.0)