다차원 공간 파일
여러 개의 필드를 동시에 키로 사용한 파일
(다중 키 파일: 여러 개의 필드 중 하나를 키로 사용한 파일, 나머지 한 키는 사실상 포인터 역할)
PAM: 점 데이터를 저장 검색
Ex) k-d트리, k-d-b트리, 격자 파일
SAM: 선,면과 같은 다차원 도형 데이터 검색
Ex) R트리, R+트리, BR트리
K-D트리
이원 탐색 트리를 다차원 공간으로 확장한 것
- 트리의 레벨에 따라 차원을 번갈아가며 비교
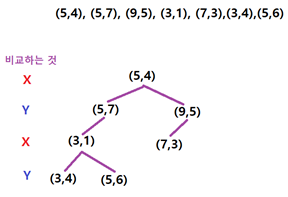
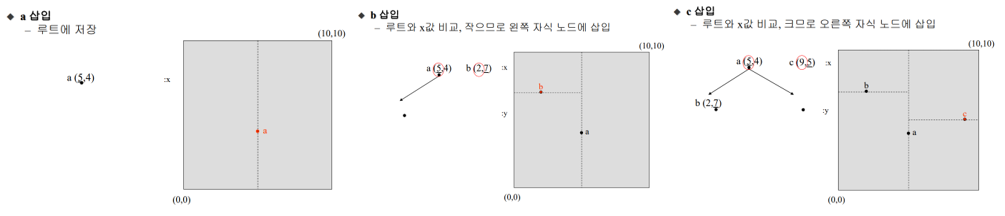
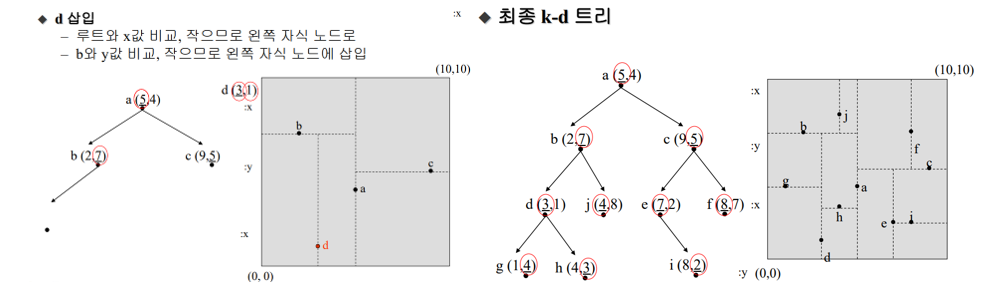
K-D트리의 검색
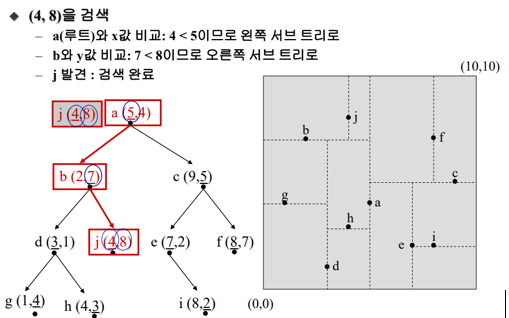
K-D트리의 단점
편향 트리가 발생할 수 있음 -> 검색 비효율적
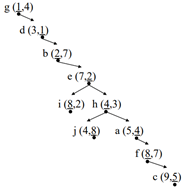
K-D-B 트리
k-d트리 + B트리
- 각 페이지를 노드로 갖고, 페이지 ID를 노드 포인터로 갖는 다원 탐색 트리
- 모든 영역은 겹치지 않고 분리, 높이는 균형돼있음
2-D-B 트리의 예시
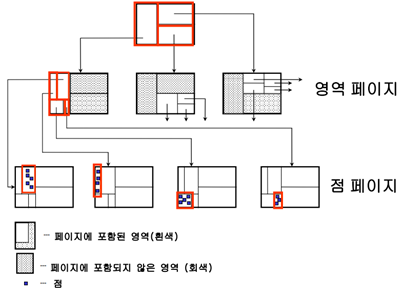
영역 페이지: 영역, 페이지ID
점 페이지: 점(실제 데이터), 점의 주소
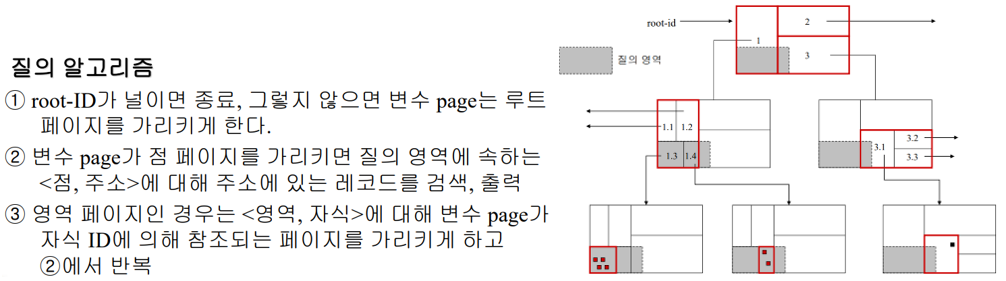
k-d-b트리의 검색
부분 범위 질의: 질의 영역이 모두 범위
Ex) 키는 170~180이고 몸무게는 60~70
부분 일치 질의: 일부 간격이 점이고, 나머지가 범위
Ex) 키는 170~180이고 몸무게는 65
완전 일치 질의: 모든 간격들이 점
Ex) 키는 175이고 몸무게는 65
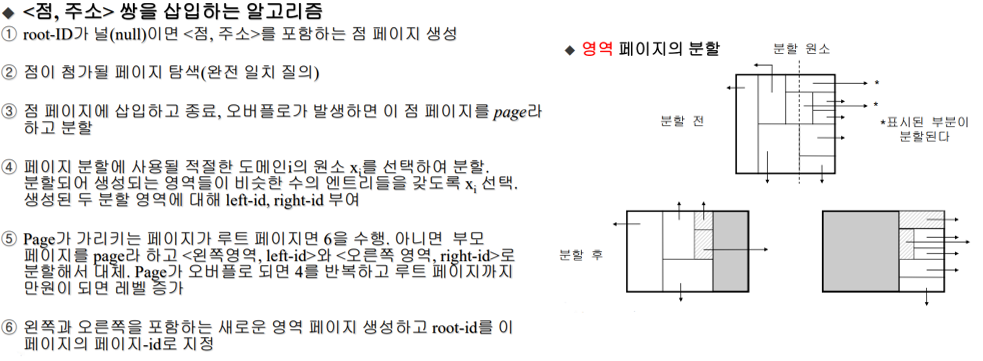
k-d-b트리의 삽입
k-d-b트리의 삭제
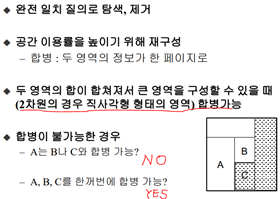
격자 파일
전체 공간을 하나 이상의 격자로 분할
특징: 디스크 기반(대용량 데이터 처리), 해시 기반
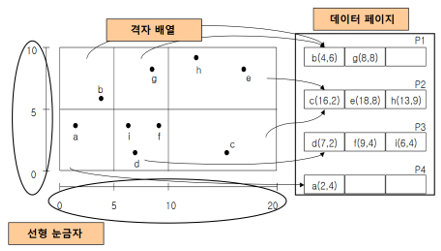
(데이터 페이지 = 실제 데이터가 저장되는 장소)
두 개 이상의 격자 블록이 하나의 데이터 페이지 공유 가능
선형 눈금자- 주기억장치에 유지, 격자배열,데이터 페이지-디스크에 위치
격자 파일의 레코드 삽입
(가정: 하나의 데이터 페이지는 최대 3개의 데이터 저장)
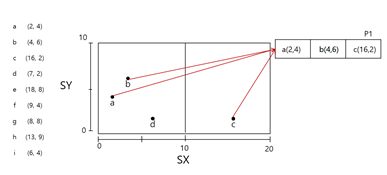
a,b,c까지는 문제 없음 -> d부터 오버플로우 생김 -> x축 반으로 나누고 데이터 분할
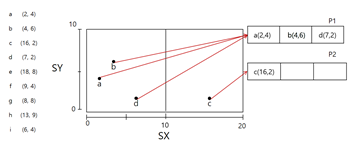
분할한 뒤 d를 올바른 위치(p1)에 삽입
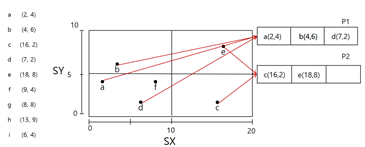
e까지는 문제 없음 -> f가 P1에 들어가야 되는데 오버플로우 생김 -> y축 반으로 나누고 데이터 분할(p1만 분할)
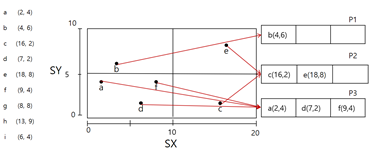
분할한 뒤 f를 올바른 위치(p3)에 삽입
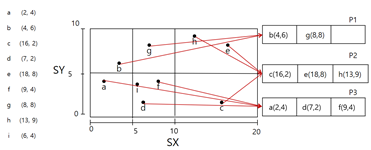
g,h까지는 문제 없음 -> i가 P3에 들어가야 되는데 오버플로우 생김 -> x축 다시 반으로 나누고 데이터 분할(p3만 분할)
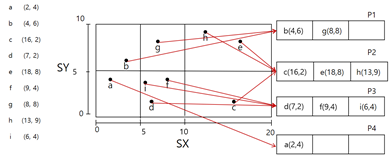
분할한 뒤 i를 올바른 위치(p3)에 삽입
격자 파일의 검색
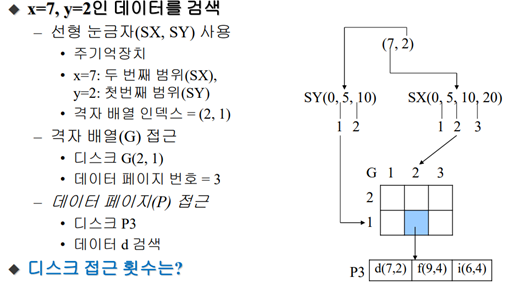
- 선형 눈금자를 통해 격자 배열 G의 인덱스 값(SX:2, SY:1)을 결정
- 격자 블록이 가리키는 해당 페이지 번호 P3을 검색
- P3에서 위치 (7,2)의 점 데이터 검색
격자 배열 접근(1번) + 데이터 페이지 접근(1번) = 총 디스크 2번 접근
격자 파일의 삭제
(삭제는 삽입의 역순으로 진행/ 삭제함 -> 선이 홀수개 -> x=k1인 선을 없애고 합병 가능성 추론, 선이 짝수개 -> y=k2인 선을 없애고 합병 가능성 추론)
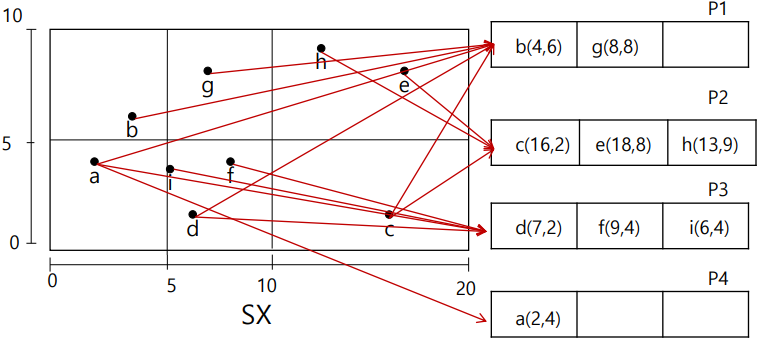
1. i가 사라지면서 구분 선이 사라짐, P3,P4는 하나의 페이지 P3로 합병
2. h,g 사라지면서 데이터 페이지에서 빠짐
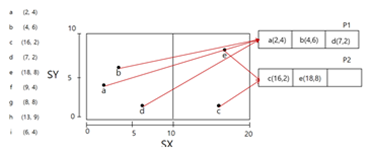
3. f가 사라지면서 구분 선이 사라짐, P1은 두 개의 격자 블록이 공용 하다 하나가 사용
4. E 사라지면서 데이터 페이지에서 빠짐
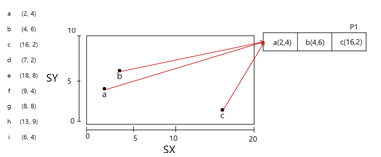
5. D가 사라지면서 구분 선이 사라짐, 데이터 세 개 남았으니 데이터 페이지 한 개만 사용
6. C,B,A 순서대로 삭제하면 끝
격자 파일의 장단점
- (격자 배열의)인덱스의 각 키들이 균등하게 분포되어 있을 때 효율적이다
- 페이지 오버플로우에 의해 분할할 필요가 없는 격자 블록까지 분할될 수 있음
- 격자의 합병 비용이 많이 듦
사분 트리
공간을 순환적으로 분해하는 계층적 자료구조
공간의 분해 원칙
Image space hierachy: 각 레벨마다 공간을 일정 크기의 동일한 부분들로 분해
Object space hierarchy: 입력 자료 값에 따라 서로 다른 크기의 공간으로 분해

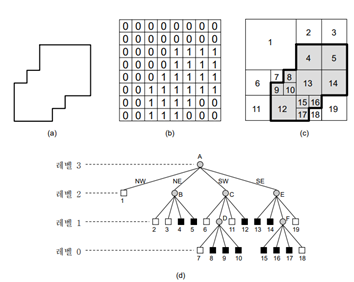
자식 노드가 나타내는 것: 부모 영역을 4영역으로 분할 했을 때, (북서)-(북동)-(남서)-(남동)
점 사분 트리

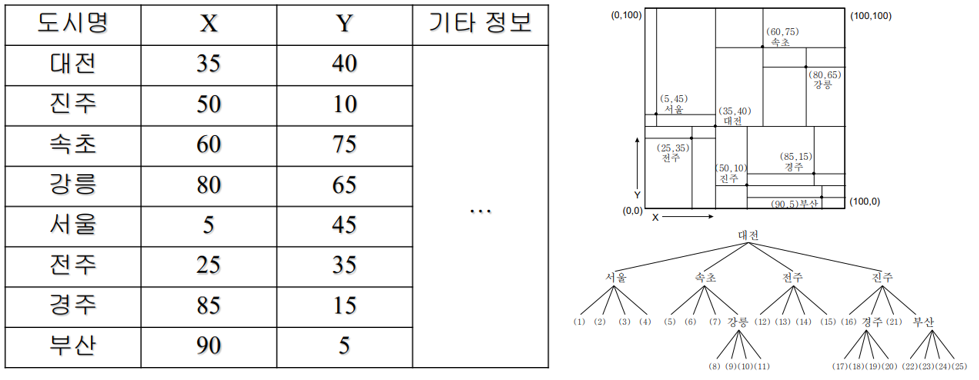
어떤 점을 기준으로 항상 네 개의 사분면이 만들어짐 -> 점 사분트리
최적의 점 사분트리: 균등하게 분포된 점 사분트리
점 사분트리의 검색
- 한 레벨 아래로 내려갈수록 탐색 공간은 1/4로 감소!
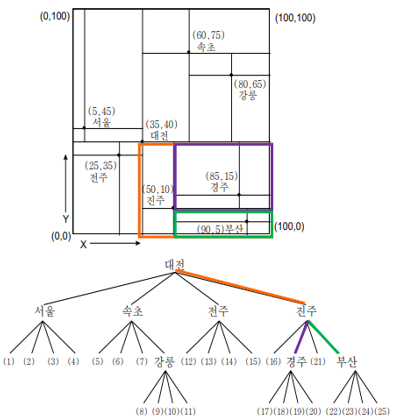
(80,65)에 위치한 도시를 검색하라
: 대전의 NE -> 속초의 SE
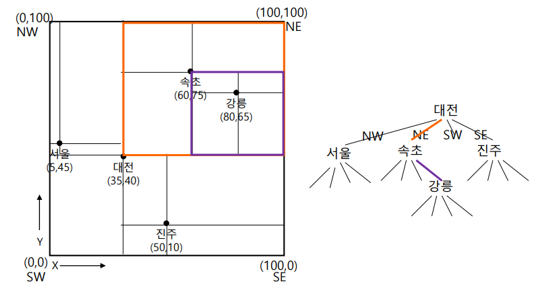
(95,8)인 도시를 검색하라
: 대전의 SE -> 진주의 SE -> 부산의 NE -> 버킷 23을 조사
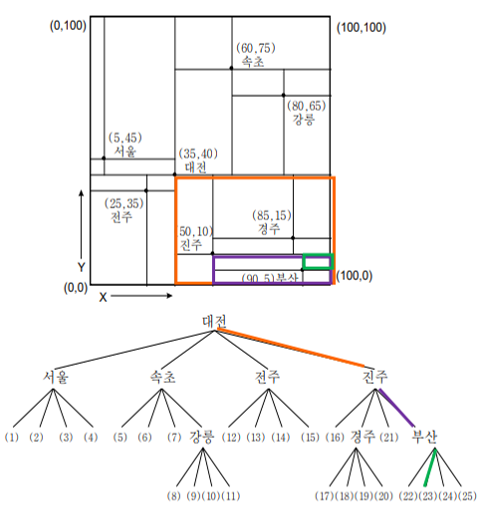
(83,10)에서 거리8이내에 존재하는 모든 도시를 검색하라
: 대전의 SE -> 진주의 NE와 SE -> 버킷 17~20, 22~25를 조사
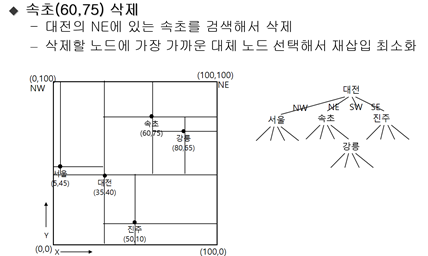
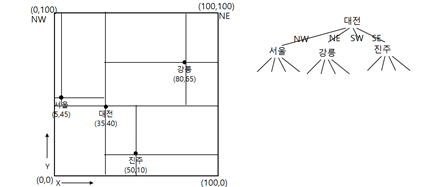
점 사분트리의 삭제
R트리
B트리를 다차원으로 확장시킨 완전 균형 트리
선,면,도형 등 다양한 다차원 공간 데이터 저장 가능
MBR: 복잡한 공간 도형을 저장하기 위해 이용하는 것
객체를 둘러싸는 최소의 정사각형을 지정함
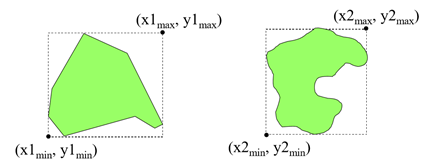
분할되는 기준점: 분할할 때 경계 사각형의 크기를 최소로 한다. (아래는 한 영역 객체(R)에 [세 개의 실제 객체(r)나 세 개의 영역 객체]가 올 수 있다)
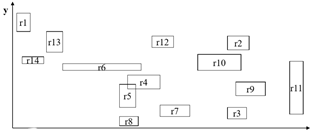
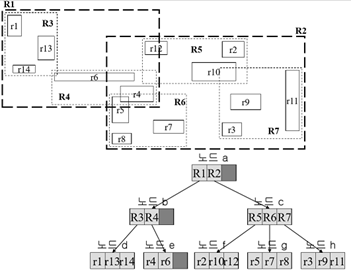
R트리의 검색
– 영역 검색 질의
루트부터 비교 (R1, R2)
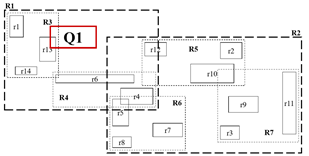
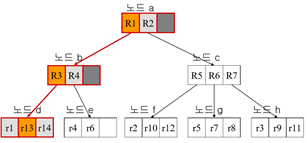
한 레벨씩 내려가면서 Q1과 RN이 겹치는지 안 겹치는지 확인 / 답은 리프 노드에
동시에 겹치는 상황: 오버랩
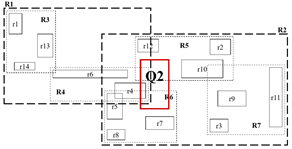
오버랩인 상황에서는 두 노드를 모두 가봐야 됨!
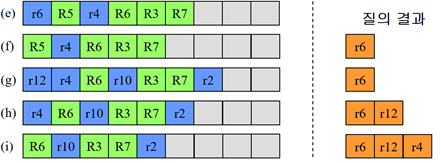
답: 리프노드 e의 r4
K-NN 질의
질의점으로부터 가장 가까운 K개의 데이터를 검색 / 우선순위 큐를 이용한다.
질의점과의 거리를 d라고 할 때, d가 작을수록 우선순위가 높음
(k=3일때 예시)
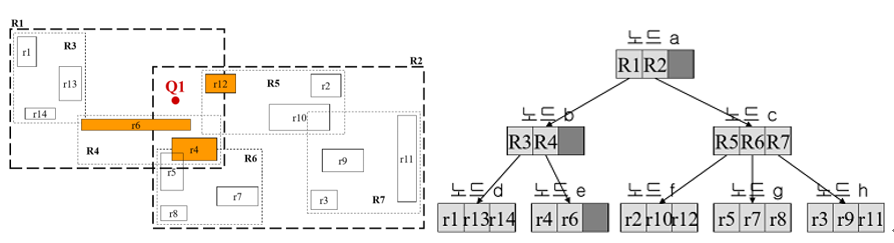
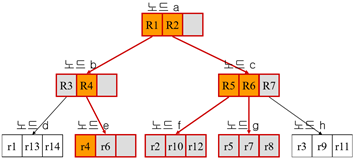
루트노드(R1,R2)부터 비교 <루트안에 속했을 때, 거리는 0으로 지정>
-> 둘 다 겹치는 상황
-> 가장 먼 곳까지의 거리를 비교했을 때 더 작은 곳이 가깝다고 지정
(R1의 r1, R2의 r11과 비교했을 때, r1과의 거리가 가까우니 R1이 가깝다고 지정->큐에 R1,R2배치)
-> R1 삭제, R1에 있던 R3와 R4를 삽입 (우선순위가 높은 R4가 앞으로 감)
-> R2 삭제, R2에 있던 R5와 R6,R7을 삽입 (우선순위가 높은대로 배치함: R4~R7)
-> R4 삭제, R4에 있던 r6와 r4를 삽입 (우선순위가 높은대로 배치함:r6~r7)
-> r6 삭제 (실제 객체 1개를 찾음)
-> 실제 객체를 k개 찾을 때까지 반복
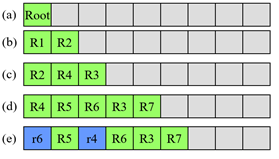
R트리 삽입


-> 면적 최소
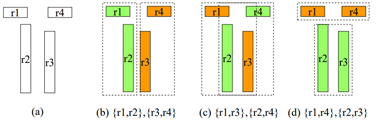
-> (d)가 가장 분할을 잘했다고 봄
(d)가 둘러쌓는 영역이 가장 작기 때문
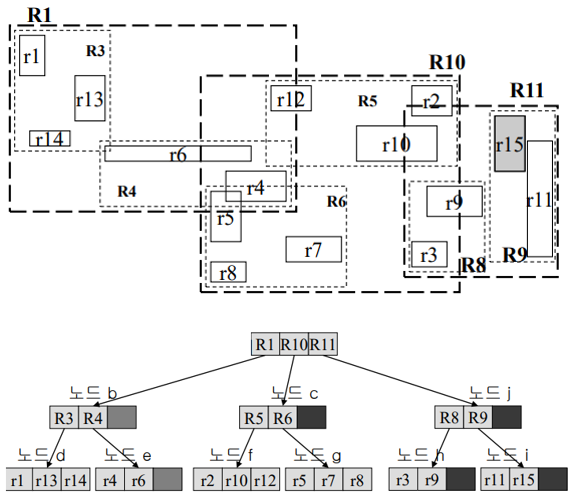
(예시) r15객체가 들어온 경우
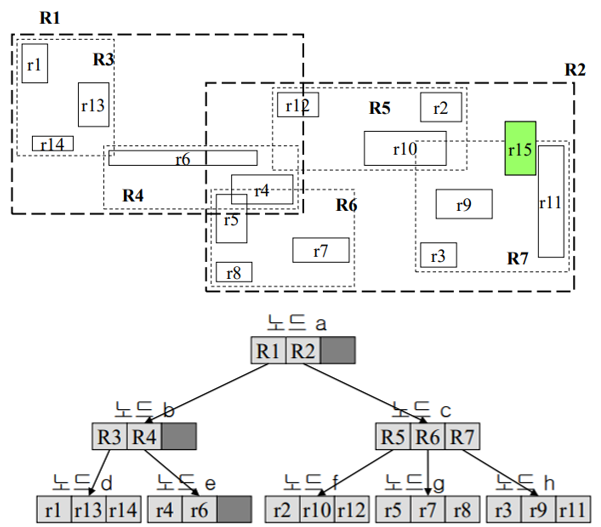
- R7영역에 삽입했을 때, 커지는 공간이 가장 작음: R7선텍
- 이미 객체가 다 차서 노드h에서 오버플로우 발생 -> R7영역을 2개,2개로 분할
- R8(r3,r9)와 R9(r15,r11)로 분할 <공간을 작게 분할>
- R7을 R8,R9로 분할했더니 이번에는 노드c에서 오버플로우 발생 -> R2영역을 2개,2개로 분할
- R10(R5,R6)와 R11(R8,R9)로 분할 <공간을 작게 분할>
- 아래가 최종 결과
R트리 삭제

R트리 분석

포함과 겹침 관계가 중요
-> 포함과 겹침이 적을수록 좋음
