임의 접근 파일 = 직접 파일
-> 다른 레코드를 참조하지 않고도 개개 레코드에 접근 가능
<-> 순차 접근 파일: 어떤 레코드 접근을 위해 그 레코드의 전위 레코드를 검색해야 됨
상대 파일 – 레코드의 키(cow,zebra,..)와 레코드의 위치(레코드 번호:상대 주소) 사이에 설정된 관계를 통해 레코드에 접근
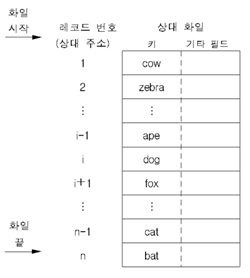
사상함수 (레코드의 위치를 찾는 함수- 입력: 키 값, 출력: 주소)

– 디렉터리 검사
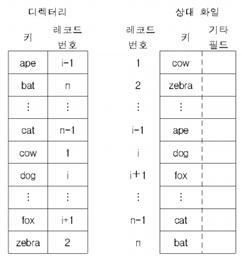
검색 절차: 디렉토리에서 키 값 검사 -> 키 값에 대응되는 레코드 번호(상대 주소) 구함 ->
사용자는 상대 주소로 레코드 접근 [즉 배열을 이용한 방법]
해싱
(계산을 통한 상대 파일 구성법)

<막대한 공간 낭비> -> 실제 필요한 주소에 비해 키 값 공간이 너무 커서 비효율적임

<빠른 접근 시간>
-> 넓은 키를 작은 주소로 변환한 뒤 그 변환 주소의 공간에 레코드를 매핑함으로써 공간도 효율적으로 쓰고 탐색 시간도 빠르게 바꿈
H(키 값) -> 주소
키 값들을 한정된 주소 공간으로 균등하게 분산시키는 것이 핵심
버킷: 레코드 저장이 가능한 (하나의 주소를 가진) 저장 구역 (블록이랑 비슷하다고 생각)
- 둘 이상의 레코드 저장 가능
- 버킷의 크기가 2면 레코드 A,B가 주소2를 가리켜도 오버플로우는 발생하지 않음 (충돌은 발생)
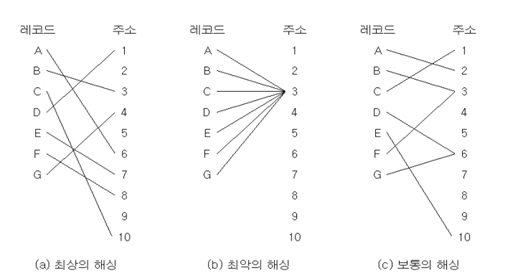
<충돌>
두 개의 상이한 레코드가 똑같은 버킷으로 해싱되는 것
동거자: 같은 주소로 해싱되어 충돌된 키 값들
<오버플로>
버킷이 만원 되었는데 저장해야 되는 경우
<해싱을 이용한 파일 설계시 고려사항>
1. 버킷 크기
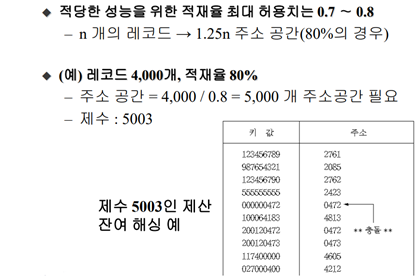
2. 적재율 (총 저장 용량에 대해 실제로 저장되는 레코드 수의 비율)
3. 해싱 함수 (레코드 키 값으로부터 주소를 생성하는 방법)
4. 오버플로 해결 방법 (주어진 공간이 만원이 된 경우의 해결 방법)
버킷 크기를 크게 하면 장단점은?
장점: 오버플로 감소
단점: 저장 공간 효율 감소, 버킷 내 레코드 탐색 시간 증가

적재 밀도가 높아지는 경우, 삽입 시 접근 수: 증가 (이미 레코드가 저장된 주소에 해싱될 경우가 많음)
적재 밀도가 높아지는 경우, 검색 시 접근 수: 증가 (원하지 않는 레코드가 저장된 주소에 해싱될 경우가 많음)
적재 밀도가 높아지는 경우, 공간 효율: 증가(경제적)
실험적으로 적재 밀도가 70% 이상일 때 충돌이 잦음
총 정리- 말로 설명: [주민번호(키),이름,나이]를 하나의 레코드라고 가정해봐. 주민번호가 10^13개까지 이론적으로 만들어질 테니 10^13개의 공간이 할당되고 거기 레코드가 띄엄띄엄 저장돼 있을거 아니야? 왜냐고? 사람 수가 아직 10^13명이 안 되니까. 그니까 겁나 메모리 낭비란 말이지. 딱 키의 개수만큼만 저장하면 되는거잖아. 그래서 어떻게 하느냐? 주민번호(키)를 메모리 상의 주소로 바꾸는거지. 예를 들어 (0011281010124)를 (10123)이런 식으로 말이지. 그리고 M[10123]에 (주민번호,이름,나이)를 저장하는거야. 이 과정을 모든 키에 대해서 하면 어떻게 되겠어? 주소가 키의 개수만큼 생성될테고, 그렇게 만들어진 주소들에 레코드들이 매핑될 테니 공간 낭비가 확 줄어들겠지. 물론 탐색 시간도 빨라질거고. 이게 해싱이야. 근데 문제는 뭐냐? 키를 주소로 바꾸다 보니 중복된 주소 값이 나올 수 있는거지. 이를 충돌이라고 해. 그래서 중복된 공간에 여러 레코드를 집어 넣었는데 그 공간이 어느순간 다 차 버린거지. 이를 오버플로라고 해. 이런 경우를 해결하면서 해싱 문제를 풀어야 되는거야!
해싱 함수

해싱 함수의 종류
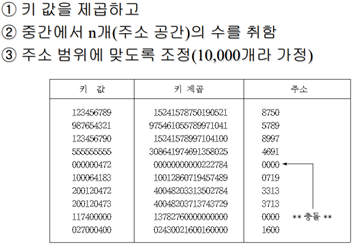
1. 제산 잔여 해싱

2. 중간 제곱 해싱
3. 중첩 해싱
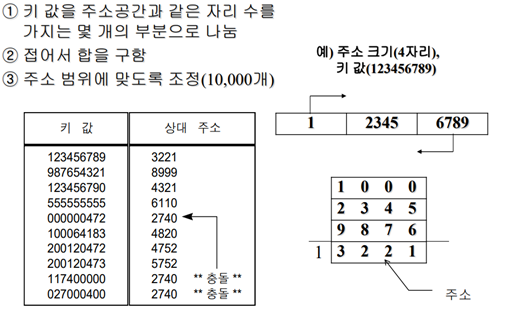
주소 크기 자리 수만큼 나눔 -> 뒤에서 앞으로 접음 -> 합을 구함
4. 숫자 추출

5. 숫자 이동 변환
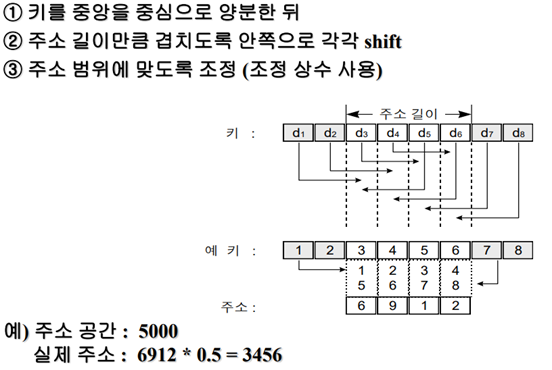
1234 오른쪽으로 2번 시프트, 5676을 왼쪽으로 2번 시프트 -> 더함
6. 진수 변환

10진수를 11진수로 바꾸기
해싱해서 만들어진 오버플로 해결법
선형조사
오버플로 발생 시, 홈 주소로부터 차례로 조사해서 가장 가까운 빈 공간을 찾는 방법 – 원형 탐색 (원형 큐에 삽입,삭제하는 것 생각)
- 레코드 검색 시에도 선형 조사(원형 탐색)을 사용해야 함
- 홈 주소에서 멀 경우 많은 조사 필요
- 삭제로 인해 만들어진 빈 공간으로 검색 시 선형조사가 단절될 수 있음 -> 삭제 표시 이용
선형조사의 단점
- 환치: 한 레코드가 다른 레코드의 주소에 저장되는 것
- 2-패스 파일생성으로 대응함
2-패스 파일 생성
1- 충돌이 일어나는 동거자들은 바로 저장하지 않고 임시 파일에 저장
2- 임시 파일에 저장해 둔 동거자들을 선형 조사를 이용해 파일에 모두 적재
독립 오버플로 구역
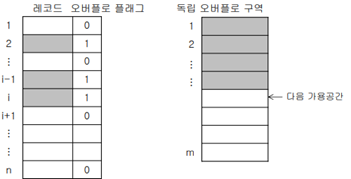
별개의 오버플로 구역을 할당해 홈 주소에서 오버플로된 모든 동거자들을 순차로 저장하는 방법
–>환치 문제를 제거
단점: 오버플로된 동거자를 접근하기 위해서는 오버플로 구역에 있는 모든 레코드들을 순차 탐색
이중 해싱

동거자 체인
연결 리스트를 써서 오버플로된 레코드들을 연결함
장점: 환치 제거
단점: 각 주소가 링크 필드를 포함하도록 확장해야 함
오버플로우 처리 기법들의 성능 비교
: 동거자 체인 > 이중 해싱 > 선형 조사
확장성 해싱 파일
- 레코드 수의 변화가 큰 경우(높은 SPAN값을 가진 파일의) 해결방안
- K: 어느 한 시점의 파일의 레코드 수 (k_min <= k <= k_max)
- SPAN: k_max / k_min

확장성 해싱
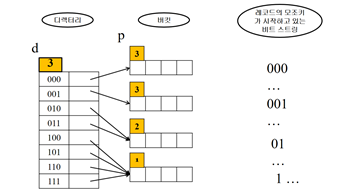
확장성 해싱 함수에 의해서 키->모조키(00000~11111)로 변환함, 디렉터리와 버핏으로 조직됨,
전역 깊이(d): 해시 값의 처음 d개 비트 수 (d는 임의 설정)
디렉터리: 2^d개만큼 포인터 공간이 할당됨, 포인터는 버킷을 가리킴, 모든 포인터가 상이한 것은 아님
버킷 깊이-(지역깊이)(p): 모조키가 공통으로 가지는 처음 비트 스트링의 길이
Ex) 모조키가 (00011,00111,01011,01010), d=3 -> (000)따서 깊이(p) 3인 버킷, (001)따서 깊이 3인 버킷, (01)따서 깊이 2인 버킷 <앞자리가 01(2개)로 같은 레코드 공간>
(아래 두 가지 경우에 따라 디렉터리와 버킷이 분할될 수 있음)
d >= p+1인 경우 분할하는 방법
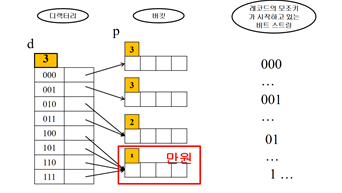
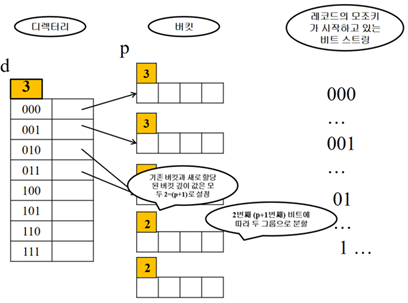
만원인 버킷의 p를 확인 -> p=1 -> p+1=2 -> 2번째 비트에 따라 두 그룹으로 분할
-> (100,101,110,111)의 두 번째 비트는 0과 1 -> [100,101]과 [110,111]으로 분할
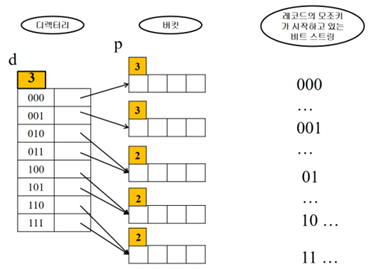
d< p+1인 경우 분할하는 방법
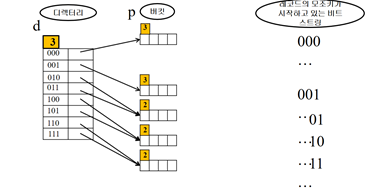
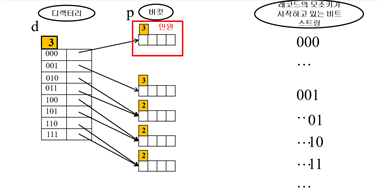
만원인 버킷의 p를 확인 -> p=3 -> p+1=4 -> 4번째 비트에 따라 두 그룹으로 분할
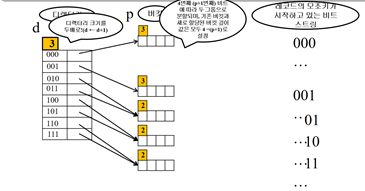
4번째 비트 생성을 위해 디렉토리 크기는 2배 늘리고 d는 1증가 -> d:4

(000) -> (0000,0001)이 됨 -> (0000,0001)의 네 번째 비트는 0과 1 -> [0000]과 [0001]로 분할
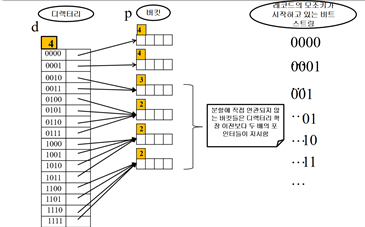
나머지 버킷들도 재분배함
총 정리
1. 키를 이용해서 모조키를 생성함 [모조키를 사용해야 분할 알고리즘이 자유롭고, 분할이 잘 돼야 가변 파일에는 이득임, 왜? 분할해서 만들어진 버킷 공간에 레코드 추가로 저장하면 되니까]
2. 모조키를 이용해서 디렉터리와 버킷을 생성함
3. 두 가지 경우의 수에 따라 디렉터리와 버킷을 다시 분할해서 정리함 [필요한 공간 할당 완료]
4. 다 정리된 버킷에 레코드를 저장함
5. 레코드의 변화가 큰 파일인 경우에도 (1~4)를 반복해서 일을 진행 시, 모조키를 이용해서 레코드를 빨리 접근할 수 있음
결론. 모조키를 이용해서 필요한 공간을 할당함으로써 가변 파일 레코드 접근을 용이하게 할 수 있다
확장성 해싱 파일의 검색
모조키의 처음 d비트를 디렉터리에 대한 인덱스로 사용하여 디렉터리에서 찾아 레코드를 접근
확장성 해싱 파일의 삭제

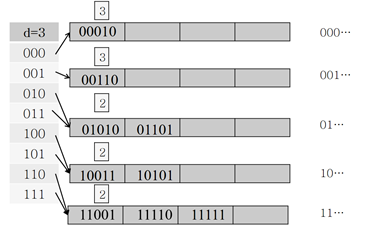
네 번째 버킷과 다섯 번째 버킷이 ‘버디 버킷’이다. 같은 키 값(2)에 (1)비트까지는 모두 같기 때문이다.
if) 11111 레코드를 삭제하겠다.
- (버디 버킷을 가지고 있으니) 네 번째 버킷의 p를 1로 바꾸고 병합한다.
- 나머지 버킷은 반환한다.
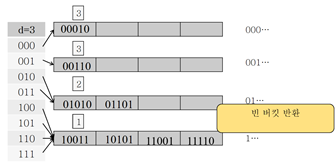
동적 해싱
(버킷의 크기가 C, 버킷의 개수가 N)

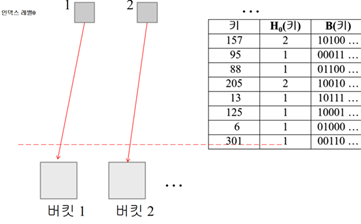
두 개의 해싱 함수 사용: H0과 B
H0: 키를 저장할 버킷 결정
B: 트리의 분기 결정
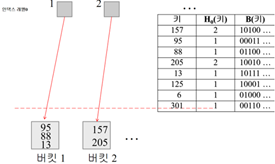
H0보고 버킷에 삽입함 -> 125부터 오버플로되서 삽입 불가됨
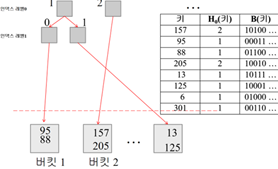
버킷1의 레코드 세 개(95,88,13)와 125레코드의 첫 번째 비트를 비교함 -> 첫 번째 비트를 기준으로 버킷을 나눔(버킷 새로 만들고 나눔) -> 이진 트리 형태가 생성됨
(이후) -> 6이 버킷 1에 삽입 됨 -> 301이 버킷1에 들어가려고 하는데 오버플로 발생함
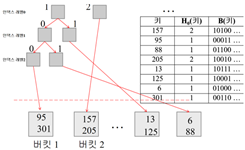
버킷1의 레코드 세 개(95,88,6)와 301레코드의 두 번째 비트를 비교함 -> 두 번째 비트를 기준으로 버킷을 나눔(버킷 새로 만들고 나눔) -> 이진 트리가 확장됨
