AVL트리
모든 노드에 대해서 왼쪽 부분 트리와 오른쪽 부분 트리의 높이 차가 1 이하인 이진 탐색 트리

트리의 균형 상태: 균형 인수(왼쪽 부분 트리의 높이 -오른쪽 부분 트리의 높이)가 1,0,-1을 만족
트리의 불균형 상태: 균형 인수가 1 초과 or -1 미만

시간복잡도
한 레벨 씩 내려가며 삽입,삭제 연산 (높이 시간) ->
균형 인수(balance) 깨지는 것 발견 (상수 시간) ->
회전(Rotation) 처리 (상수 시간) -> AVL 트리의 연산은 O(logn)
// AVL 트리의 높이는 O(logn)

코딩 테스트 예시

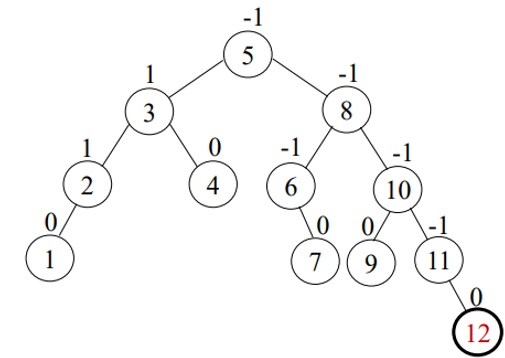
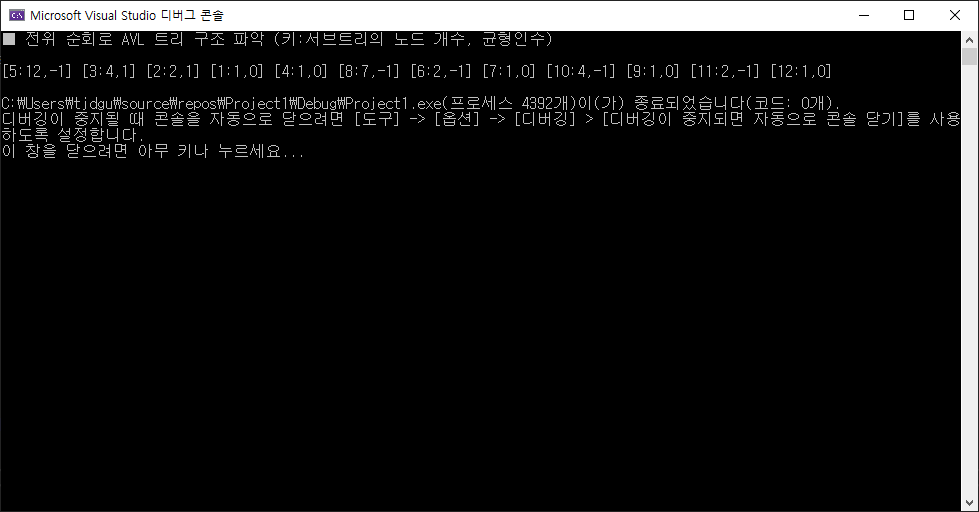
size_field: [1:1], [2:2], [3:4], [4:1], [5:12], [6:2], [7:1], [8:7], [9:1], [10:4], [11:2], [12:1]
// [키 값: 서브 트리의 노드 개수]

#include <stdio.h>
#include <stdlib.h>

typedef struct AVLNode {
    int key;
    int size_field;
    int height; 
    int balance;
    struct AVLNode* left;
    struct AVLNode* right;
}AVLNode;
typedef AVLNode* AVLNode_ptr;

// MAX 함수
int MAX(int a, int b) {
    return a > b ? a : b;
}

// 트리의 높이 구하기 
int get_height(AVLNode_ptr T) {
    if (T) {
        // 트리의 높이 = MAX(오른쪽 서브트리의 높이, 왼쪽 서브트리의 높이) +1
        int tmp = MAX(get_height(T->left), get_height(T->right));
        return 1 + tmp;
    }
    else
        return 0;
}

// 노드의 균형인수(왼쪽 서브트리의 높이 - 오른쪽 서브트리의 높이) 구하기
int get_balance(AVLNode_ptr T) {
    if (T)
        return get_height(T->left) - get_height(T->right);
}

// 노드 생성 함수
AVLNode_ptr create_node(int key) {
    AVLNode_ptr node = (AVLNode_ptr)malloc(sizeof(AVLNode));
    node->key = key;
    node->size_field = node->balance = node->height = 0; // update 함수에서 일괄 처리함 
    node->left = node->right = NULL;
    return node;
}

// 오른쪽으로 회전시키는 함수 (왼쪽 -> 오른쪽)
// LL과 LR,RL에 쓰임 
AVLNode_ptr rotate_right(AVLNode_ptr parent) {
    AVLNode_ptr child = parent->left;
    parent->left = child->right; // child의 서브 트리 한 쪽을 parent가 가져감 
    child->right = parent; // 오른쪽 회전 

    return child;
}

// 왼쪽으로 회전시키는 함수 (오른쪽 -> 왼쪽)
// RR과 LR,RL에 쓰임
AVLNode_ptr rotate_left(AVLNode_ptr parent) {
    AVLNode_ptr child = parent->right;
    parent->right = child->left; // child의 서브 트리 한 쪽을 parent가 가져감 
    child->left = parent; // 왼쪽 회전 

    return child;
}

// AVL 트리 삽입
AVLNode_ptr insert_node(AVLNode_ptr T, int key) {
    // 이진 탐색 트리의 노드 추가 수행
    if (T == NULL)
        return create_node(key);

    if (key < T->key)
        T->left = insert_node(T->left, key);

    else if (key > T->key)
        T->right = insert_node(T->right, key);

    else // 동일한 키는 허용하지 않음
        return T;

    // 노드의 균형인수 계산
    int balance = get_balance(T);

    /*
    * 회전 (삽입 시 불균형이 발생하면 진행)

    - X: 불균형이 탐지된 가장 가까운 조상 노드

    - LL 타입 처리
    X 기준으로 (왼쪽 -> 오른쪽 회전)

    - RR 타입 처리
    X 기준으로 (오른쪽 -> 왼쪽 회전)

    - LR 타입 처리
    X의 왼쪽 자식 기준으로(오른쪽 -> 왼쪽 회전) -> X 기준으로 (왼쪽 -> 오른쪽 회전)

    - RL 타입 처리
    X의 오른쪽 자식 기준으로 (왼쪽 -> 오른쪽 회전) -> X 기준으로 (오른쪽 -> 왼쪽 회전)
    */

    // LL 타입 처리
    if (balance > 1 && key < T->left->key)
        return rotate_right(T);

    // RR 타입 처리
    if (balance < -1 && key > T->right->key)
        return rotate_left(T);

    // LR 타입 처리
    if (balance > 1 && key > T->left->key) {
        T->left = rotate_left(T->left);
        return rotate_right(T);
    }

    // RL 타입 처리
    if (balance < -1 && key < T->right->key) {
        T->right = rotate_right(T->right);
        return rotate_left(T);
    }

    return T;
}

// 트리에 size_field(부분트리에 속한 노드의 개수), balence(균형인수) 부여하기 
// postorder 응용해서 제작함 
void update(AVLNode_ptr T) {
    if (T) {
        update(T->left);
        update(T->right);

        // 잎 노드
        if ((T->left == NULL) && (T->right == NULL)) { 
            T->size_field = 1;
            T->height = 1;
            T->balance = 0;
        }

        // 내부 노드 
        else { 
            if ((T->left != NULL) && (T->right != NULL)) {
                T->size_field = 1 + (T->left->size_field) + (T->right->size_field);
                T->height = 1 + MAX(T->left->height, T->right->height);
                T->balance = (T->left->height) - (T->right->height);
            }
            else if ((T->left != NULL) && (T->right == NULL)) {
                T->size_field = 1 + (T->left->size_field);
                T->height = 1 + (T->left->height);
                T->balance = (T->left->height) - 0;
            }
            else {
                T->size_field = 1 + (T->right->size_field);
                T->height = 1 + (T->right->height);
                T->balance = 0 - (T->right->height);
            }
        }

    }
}

// 전위 순회 함수 
void preorder(AVLNode_ptr T) {
    if (T) {
        printf("[%d:%d,%d] ", T->key, T->size_field, T->balance);
        preorder(T->left);
        preorder(T->right);
    }
}

int main(void) {
    AVLNode_ptr root = NULL;

    root = insert_node(root, 8);
    root = insert_node(root, 9);
    root = insert_node(root, 10);
    root = insert_node(root, 2);
    root = insert_node(root, 1);
    root = insert_node(root, 5);
    root = insert_node(root, 3);
    root = insert_node(root, 6);
    root = insert_node(root, 4);
    root = insert_node(root, 7);
    root = insert_node(root, 11);
    root = insert_node(root, 12);

    update(root); // 각 노드에 서브트리의 노드 개수와 균형인수 부여하기 

    printf("■ 전위 순회로 AVL 트리 구조 파악 (키:서브트리의 노드 개수, 균형인수)\n\n");
    preorder(root);
    printf("\n");

    return 0;
}