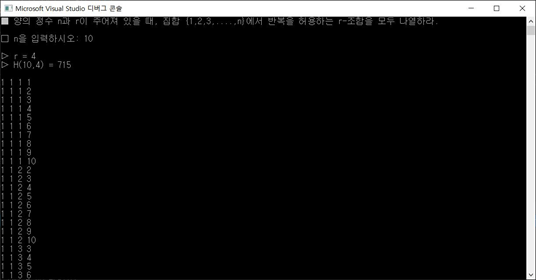
양의 정수 n과 r이 주어져 있을 때, 집합 {1,2,3,….,n}에서 반복을 허용하는 r-조합을 모두 나열하라
#include <stdio.h>
int n, r, *set, *out;
int count = 0;
// 팩토리얼 함수
int factorial(int a, int b) {
if (a == 0)
return 1;
else {
int result = 1;
for (int i = a; i > b; i--)
result *= i;
return result;
}
}
// 중복 조합 개수 구하는 함수
int over_combi_num(int n, int r) {
int temp = n; // n을 임의로 저장
n = n + r - 1; // h(n,r)=c(n+r-1,r)이므로 인수 n만 n+r-1로 바꿔줌
if (r >= 0 && r <= n) {
int denominator, numerator, answer;
denominator = factorial(n, n - r);
numerator = factorial(r, 0);
answer = denominator / numerator;
printf("▷ H(%d,%d) = %d\n\n", temp, r, answer); // 출력할 때는 원래 n사용
}
}
// 중복 조합 나열하는 함수
void over_combination(int start, int end, int index) {
// r이 0이면 처리 안 함
if (r == 0)
return 0;
int i;
// end가 0이면 out배열이 다 찼으니 출력
if (end == 0) {
for (i = 0; i < start; i++) {
printf("%d ", out[i]);
}
printf("\n");
count++;
}
// 이 else if는 두 번째 over_combination이 호출돼야지만 실행될 수 있음
// 이게 실행됐다는 것은 set의 마지막 원소까지 out에 주었다는 것이고,
// 재귀에 의해 out[r-1]=set[n-1]까지 완료됐다는 것을 의미
// 더 이상 할게 없으니 리턴함
else if (index == n) {
return;
}
else {
out[start] = set[index];
// 출력할 내용을 담는 배열 out에 값을 주기
over_combination(start + 1, end - 1, index); // index 고정해서 같은 값 들어가게 설정
// 계속 앞에 있는 것 r개만 주면 안 되니, start는 고정, index를 증가
over_combination(start, end, index + 1);
}
}
void main()
{
printf("■ 양의 정수 n과 r이 주어져 있을 때, 집합 {1,2,3,....,n}에서 반복을 허용하는 r-조합을 모두 나열하라.\n");
printf("\n□ n을 입력하시오: ");
// n 입력 받기
scanf_s("%d", &n);
// n값을 이용해서 set 지정
set = (int*)malloc(sizeof(int)*n);
for (int i = 0; i < n; i++)
set[i] = i + 1;
// r만들기 (0~n-1)
srand(time(NULL));
r = rand() % n;
printf("\n▷ r = %d\n", r);
// r이 0일 때 메모리 할당하면 오류 걸리니 패스
if (r != 0)
out = (int*)malloc(sizeof(int)*r);
// 중복 조합 문제 풀기
over_combi_num(n, r);
over_combination(0, r, 0);
printf("\n◈ 조합 나열한 것 카운트 = %d\n", count);
// 메모리 할당 해제
free(set);
free(out);
}
확률 코드 패키지
조합 사전 순으로 나열하기
중복 조합 사전 순으로 나열하기
중복 순열 사전 순으로 나열하기
순열 사전 순으로 나열하기
