나이브 베이즈는 스팸 메시지 필터를 만들 때 사용됩니다.
스팸의 유래를 소개하며 포스팅을 시작하겠습니다.

스팸의 유래)
스팸이라는 회사에서 자기네 햄을 알리려고 쓸데없는 메일을 많이 보냄
이후부터 쓸데없는 메일/문자를 스팸이라고 함
스팸이 아닌 메일/문자는 햄이라고 함

스팸 문제는 ‘확률 및 통계’에서도 다룹니다.
아래는 확률과 통계의 독립 사건에 대한 이야기입니다.

독립 사건에서의 결합 확률)
P(A  ∩ B)=P(A)*P(B)

전체 메시지 중 스팸의 비율이 20%이고 전체 이메일 중 ‘당일’이 포함된 비율이 5%라고 하면
두 사건이 독립일 때 ‘당일’이 포함되면서 스팸일 가능성은 0.1임
하지만 이 둘이 독립이 아님

아래는 확률과 통계의 베이즈 정리에 대한 소개입니다.

베이즈 정리)
P(A|B)=P(A  ∩ B)/P(B)
P(B|A)=P(A  ∩ B)/P(A) -> P(A  ∩ B)=P(B|A)*P(A)

=> P(A|B) = P(B|A)*P(A)/P(B)

‘당일’일 때 스팸일 확률 P(스팸|당일)
= P(당일|스팸) * P(스팸) / P(당일)
‘당일’이라고 모든게 스팸은 아니라서 일반적으로 구하기 어려운데
베이즈 정리를 이용하면 쉬움! (스팸 개수 중에서 당일 개수 세는 것은 쉬우므로)

베이즈 정리에 대한 이해가 마쳤으면 아래 빈도표에서 ‘당일’이 포함된 문자가 스팸일 확률을 구해 봅시다.

P(당일|스팸) = 4/20
P(스팸)=20/100
P(당일)=5/100
P(스팸|당일) = (4/20 * 20/100) / 5/100

그러나 실제로 스팸에 자주 등장하는 단어가 한 개 이상이므로, 스팸에 자주 나올 법한 단어들이 여러 개가 나왔을 때 스팸일
확률은 P(스팸|당일  ∩ 최고  ∩ 최저  ∩ 팀장) 이 됩니다.

이것은 P(당일  ∩ 최고  ∩ 최저  ∩ 팀장|스팸) * P(스팸) / P(당일  ∩ 최고  ∩ 최저  ∩ 팀장) 으로 바꿀 수 있습니다.

하지만 교집합 확률 구하는 것은 쉽지 않습니다.

• 각각의 단어를 모든 메일에서 탐색(1, 당일 탐색, 2. 최고 탐색, 3. 최저 탐색, 4. 팀장 탐색)
• 공통된 메일 선택하기
• 위 과정에서 엄청난 메모리가 들어감

그러나 만일 각각의 사건이 독립이면 구하기가 쉬워집니다.
그래서 한 수학자가 독립은 아니지만, 독립이라고 가정(틀린 가정)을 하고 문제를 풀었습니다.
하지만 특이하게 잘 구해졌다고 합니다. (스팸을 잘 구별함)

결국 아래와 같은 식이 유도됩니다.

=> P(W|h) =  p(w1 ∩ w2 ∩ w3,…,wn|h)
= p(w1|h) ∩ p(w2|h) ∩ … ∩ p(wn|h)
= p(w1|h) * p(w2|h) * … * p(wn|h)

여기까지 이해를 마쳤다면 아래의 문제를 풀어 봅시다!

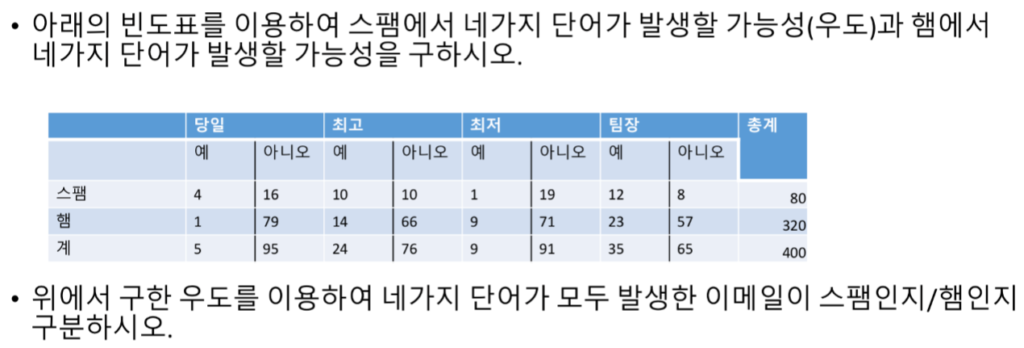
첫 번째 문제는 P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸)과 P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|햄)을 구하라는 문제입니다.

P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸)
= P(당일 |스팸) ∩ P(최고 |스팸) ∩ P(최저 |스팸) ∩ P(팀장 |스팸)
= P(당일 |스팸) * P(최고 |스팸) * P(최저 |스팸) * P(팀장 |스팸)
= (4/80) * (10/80) * (1/80) * (12/80)

P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|햄)
= P(당일 |햄) ∩ P(최고 |햄) ∩ P(최저 |햄) ∩ P(팀장 |햄)
= P(당일 |햄) * P(최고 |햄) * P(최저 |햄) * P(팀장 |햄)
= (1/320) * (14/320) * (9/320) * (23/320)

두 번째 문제는 P(스팸|당일 ∩ 최고 ∩ 최저 ∩ 팀장) 과 P(햄|당일 ∩ 최고 ∩ 최저 ∩ 팀장) 을 구하고 무엇이 더 확률이 높은지 구하라는 문제입니다.

P(스팸|당일 ∩ 최고 ∩ 최저 ∩ 팀장)
= P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸) * P(스팸) / P( 당일 ∩ 최고 ∩ 최저 ∩ 팀장 )

P(햄|당일 ∩ 최고 ∩ 최저 ∩ 팀장)
= P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸) * P(햄) / P( 당일 ∩ 최고 ∩ 최저 ∩ 팀장 )

으로 구하는게 정석이지만, 무엇이 더 확률적으로 높은지 구하는 것이고 분모부분은 같기 때문에 분모는 제외하고 구해도 됩니다!

따라서
P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸) * P(스팸)
= (4/80) * (10/80) * (1/80) * (12/80) * 80/400
= 4.6875e-07

P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸) * P(햄)
= (1/320) * (14/320) * (9/320) * (23/320) * 320/400
= 2.210999e-07

이는 스팸의 수치가 더 크므로 스팸으로 분류됩니다!

이메일은 스팸과 햄 두 가지 밖에 없으므로 완전한 식을 구한다면,

P(스팸|당일 ∩ 최고 ∩ 최저 ∩ 팀장)
= 4.6875e-07 / 4.6875e-07 + 2.210999e-07
P(햄|당일 ∩ 최고 ∩ 최저 ∩ 팀장)
= 2.210999e-07 / 4.6875e-07 + 2.210999e-07

으로 구할 수 있습니다!

다음은 ‘라플라스 추정량’을 알아 보겠습니다!

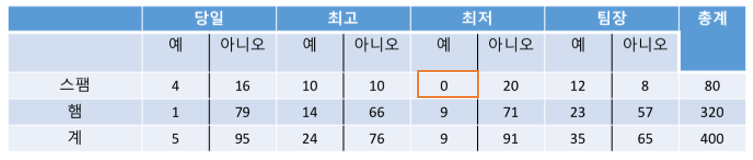
위 식에 대해서 P(당일 ∩ 최고 ∩ 최저 ∩ 팀장|스팸) 을 구한다면 어떻게 될까요?
아직 ( ‘최저’ 가 있으면서 스팸)이 없었기 때문에 0이 됩니다.

그러면 다음에 (당일, 최고, 최저, 팀장) 가 한 번에 오는 문자가 오면 무조건 햄으로 판정해야 될까요?

정답은 X입니다.

이미 (당일, 최고, 팀장)이 붙은 문자에서 스팸이 다수 발견되었기 때문에, ‘최저’가 같이 와도 스팸일 가능성이 있습니다.

이럴 경우 ‘라플라스 추정량’을 이용합니다!

0의 효과를 제거하기 위해 p(W|s)를 구할 때 분자는 각각 +1, 분모는 단어의 수를 더해주면 됩니다.
< ex) W: 나오는 문자, s: 스팸 >

P(당일 ∩ 최고 ∩ 최저 ∩ 팀장 | 스팸) * p(스팸)
= (4/80 * 10/80 * 0/80 * 20/80) * 80/400
= > (5/84 * 11/84 * 1/84 * 21/84) * 80/400

P(당일 ∩ 최고 ∩ 최저 ∩ 팀장 | 햄) * p(햄)
= (1/320) * (14/320) * (9/320) * (23/320) * 320/400
= > (2/324 * 15/324 * 10/324 * 24/324) * 320/400

다음에 ’나이브 베이즈 실습’으로 찾아 뵙겠습니다!