여러 모양이 섞여 있는 집합에서 특징 별로 구분해서 같은 종류의 도형만 남게 해봅시다.
우리는 아래와 같은 ‘의사결정나무’를 이용합니다.
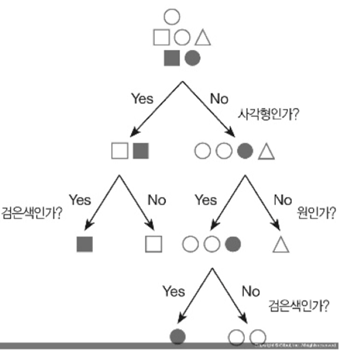
‘의사결정나무’의 규칙은 한 단계 거쳤을 때마다 좀 더 정리되게 집합을 나눠야 하는 것입니다.
이를 컴퓨터로 처리하고 싶은데 컴퓨터는 정리라는게 무엇인지 모릅니다.
그렇기에 ‘정리’라는 단어말고 컴퓨터가 처리할 수 있는 단어로 머신러닝 목표를 정해 봅시다!
이는 ‘컴퓨터에게 알려주는 학습 목표’를 정하는 것입니다.
‘머신러닝’을 이용하면 컴퓨터가 학습한 후, 다음에 비슷한 데이터가 와도 같은 방법으로 처리할 수 있습니다!
머신러닝 목표: 순도가 증가, 불순도 혹은 불확실성이 최대한 감소하도록 만들어!!
순도와 관련된 사실은 엔트로피와 지니지수를 이용할 수 있습니다.
엔트로피와 지니지수는 공식으로 나와 있으니 컴퓨터가 처리할 수 있겠죠?
엔트로피는 ‘데이터가 얼마나 섞여 있는지를 나타내는 척도’입니다.
많이 섞여 있을 수록 엔트로피 값은 1에 가까워 집니다.
이 척도를 알면 무엇을 할 수 있을까요?
예시)
엔트로피 검사(A) -> 전체 집합을 선을 그어서 나눠보기 -> 엔트로피 검사(B) -> 다른 방법으로 선을 그어서 나눠보기 -> 엔트로피 검사(C)
위 예시에서는 엔트로피 검사를 총 3번합니다.
A보다 B가 엔트로피 값이 더 작고, B보다 C가 엔트로피 값이 작으면
(더 순도가 낮다 -> 정리가 잘됐다)고 볼 수 있지 않을까요?
말로만 하면 이해가 힘드니, 예시를 통해 엔트로피를 구해 봅시다!
Entropy(A)= – Sigma(k=1->m) { Pk*log2(Pk) }
Pk= A영역에서 k범주에 속하는 레코드의 비율
M= 범주의 개수
(레코드: 원소라고 생각, 범주: 원소의 종류<빨간 원소,파란 원소>라고 생각)

A: 전체
K=빨간 색 동그라미일 때
10/16log2(10/16)
K= 파란 색 동그라미일 때
6/16log2(6/16)
Entropy(A)= – { 10/16log2(10/16) + 6/16log2(6/16) }
이를 R 프로그래밍으로 확인해봅시다!
# 범주가 두 개일 때 엔트로피 값 구하기
entropy=function(pk){
return (- pk *log2(pk) - (1-pk)*log2(1-pk) )
}
entropy(10/16)
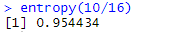
분할 후 엔트로피를 재검사하기 전에, 엔트로피의 특징도 한 번 알아 봅시다!
엔트로피의 특징
A영역에 속한 모든 레코드가 동일한 범주에 속할 경우 엔트로피가 0임
반대로 범주가 둘 뿐이고 레코드 수가 동일하게 반반씩 섞여 있을 경우 엔트로피는 최대임
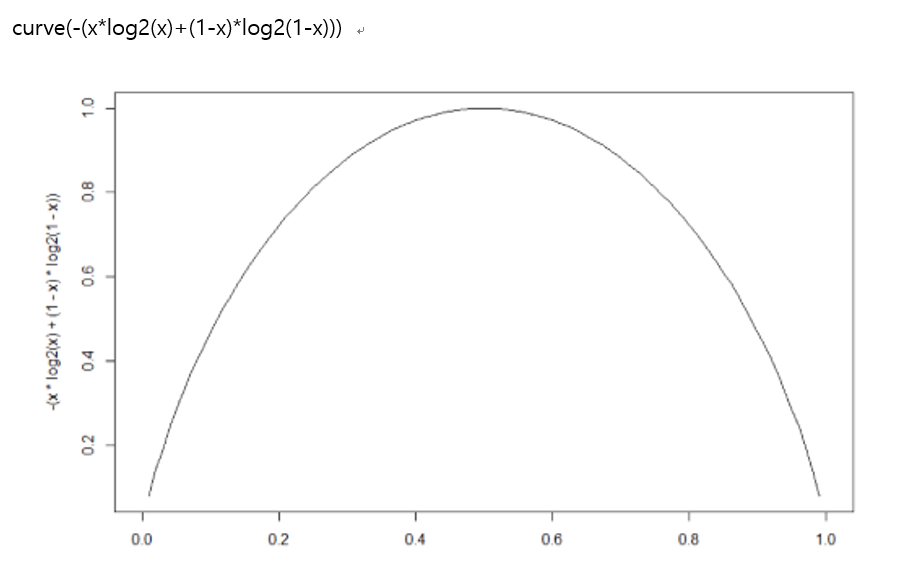
이제 분할 후 엔트로피를 구해 봅시다!
분할 후 엔트로피를 계산할 때는 다른 공식을 이용합니다!

Entropy(B)= Sigma(i=1->d) [ Ri * { – (Sigma(k=1->m)Pk*Log2(Pk)) } ]
Ri= 분할 후 i영역에 속하는 레코드 수 / 전체 레코드 수
d= 영역의 개수
식이 어려워 보이지만 쉽게 생각합시다!
범주가 두 개니까 안쪽 시그마를 [ a(k:빨강)+b(k:파랑) ] 라고 표현할 수 있습니다!
영역이 두 개니까 바깥쪽 시그마는 [ R1+R2 ] 로 표현할 수 있겠네요!
그러면 R1*(-a-b) + R2*(-a-b)가 됩니다! < a,b값은 i에 따라 달라짐 >
{ 0.5 * (-1/8 * Log2(1/8) – 7/8 * Log2(7/8) ) } + { 0.5 * (-3/8 * Log2(3/8) – 5/8 * Log2(5/8) ) }
엔트로피 함수는 위에서 만들었으니 이렇게 풀 수 있습니다!
0.5 * entropy(1/8) + 0.5 * entropy(3/8)
이를 R 프로그래밍으로 확인해봅시다!
# 범주가 두 개일 때 엔트로피 값 구하기
entropy=function(pk){
return (- pk *log2(pk) - (1-pk)*log2(1-pk) )
}
# 영역이 두 개일 때 분할 후 엔트로피 값 구하기
entropy2=function(r1,pk1,pk2){
# r1은 첫 번째 영역 레코드 비율
# pk1은 첫 번째 영역에서 한 범주의 레코드 비율
# pk2은 두 번째 영역에서 한 범주의 레코드 비율
# pk1의 엔트로피
one=entropy(pk1)
# pk2의 엔트로피
two=entropy(pk2)
return(r1 * one + (1-r1) * two)
}
# 엔트로피 함수로 (분할 후 엔트로피) 풀기!
0.5 * entropy(1/8) + 0.5 * entropy(3/8)
# 엔트로피2 함수로 (분할 후 엔트로피) 풀기!
entropy2(0.5,1/8,3/8)

분할 하기 전 엔트로피: 0.95
분할 한 후 엔트로피: 0.74
엔트로피가 줄어들었으니 분할을 잘 했다고 볼 수 있습니다!
결국 정리를 잘한게 됩니다.
다음 포스팅에는 ‘지니지수’ 를 알아 보겠습니다!
